umm_1943

∫0 dx

Пример 3. Вычислить интеграл −1 x2 или показать его расходимость.

0

dx

ε

dx

1

ε

1

1

Решение ∫

x

2

= lim

∫

x

2

= −lim

x

= −lim(

−

) = +∞.

ε→0

ε→0

ε→0

ε −1

−1

−1

−1

Вывод − интеграл расходится.

Пример 4. Вычислить интеграл ∫1

dx

или показать его расходимость.

1− x

0

Решение

1

dx

= lim

1−ε

dx

= −lim 2 1− x

1−ε

= −lim 2( ε −1) =1.

∫

∫

1 − x

ε→0

1− x

ε→0

0

ε→0

0

0

Вывод − интеграл сходится и площадь криволинейной трапеции равна 1. Аналогично определяется несобственный интеграл от функции, имеющей

разрыв второго рода на левой границе интервала интегрирования:

∫b	f (x)dx = limε→0	∫b	f (x)dx (здесь ε > 0 ).
a		a+ε

В случае, если разрыв второго рода имеет место внутри интервала интегрирования, например, в точке с, то следует разбить интервал этой точкой и рассмотреть сумму интегралов вида

∫b

f (x)dx = limε→0 c∫−ε

f (x)dx +limδ→0

∫b

f (x)dx

(здесь ε > 0, δ > 0).

a

a

c+δ

Данный интеграл сходится, если сходятся оба интеграла в правой части, и

расходится, если расходится хотя бы один из них.

Пример 5. Вычислить интеграл ∫2

dx

или показать его расходимость.

2

−1 3 (x −1)

Решение

2

dx

1−ε

dx

2

dx

= lim33 (x −1)

1−ε

(x −1)

2 =

= lim

+lim

+ lim33

∫

3 (x −1)

2

ε→0 ∫

3 (x −1)

2

δ→0 ∫

1)

2

ε→0

−1

δ→0

1+δ

−1

−1

1+δ 3 (x −

=3limε→0 (3 −ε − 3 −2 )+3limδ→0 (3 1 − 3 δ )=3(3 2 +1).

Вывод − интеграл сходится.

Геометрические приложения определенного интеграла

1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ

Принимая во внимание геометрический смысл определенного интеграла, получаем, что площадь криволинейной трапеции, ограниченной линиями

x = a; x = b; y = 0; y = f (x) , равна ∫b	f (x)dx (предполагается, что f (x) ≥ 0 ).
a

10

В более общем случае площадь фигуры, ограниченной линиями x = a; x = b; y = f1 (x); y = f2 (x) ( f2 (x) ≥ f1(x)), равна

S = ∫b ( f2 (x) − f1 (x))dx .

a

Площадь фигуры, ограниченной линиями

y = c; y = d; x =ϕ1 ( y); y =ϕ2 ( y) (ϕ2 ( y) ≥ϕ1 ( y)), вычисляется по формуле

S = ∫d (ϕ2 ( y) −ϕ1 ( y))dy .

c

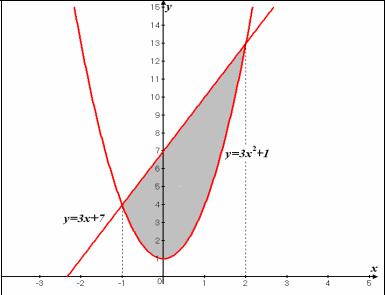
Пример 1. Найти площадь фигуры, ограниченной линиями y =3x2 +1; y =3x +7 . Построить чертеж.

Решение. Найдем точки пересечения параболы и прямой. Приравняем правые части уравнений, задающих функции, и решим полученное уравнение

3x2 +1 =3x +7

3x2 −3x −6 = 0

x2 − x −2 = 0; x1 = −1; x2 = 2.

Фигура, площадь которой

нужно найти, изображена на рисунке. Используя приведенную формулу, получим

S = ∫2 (3x +7 −3x2 −1)dx =

−1

2

2

2

)dx =

3x2

+ 6x − x

3

= (6 +12 −8)

3

−6

=

27

=13,5.

= ∫(3x + 6 −3x

−

+1

−1

2

−1

2

2

2. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ

Пусть плоская фигура ограничена линией ρ = ρ(φ) и лучами φ =φ1; φ =φ2 , тогда ее площадь можно найти по формуле

φ

S = 1 ∫2 ρ2 (φ)dφ ,

2 φ1

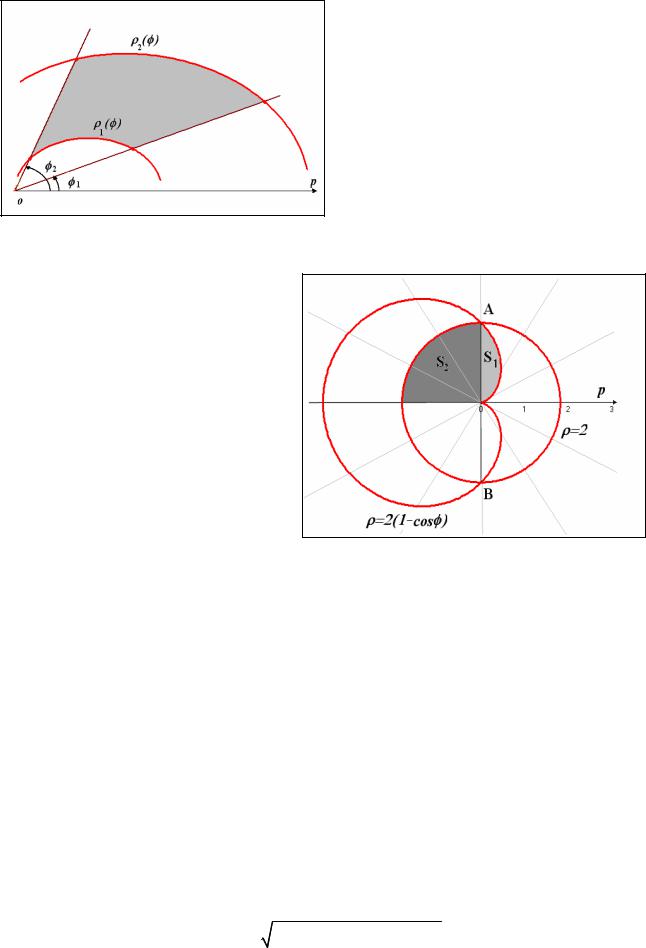
Если же фигура ограничена линиями ρ1 = ρ1 (φ); ρ2 = ρ2 (φ) и лучами φ =φ1; φ =φ2 , то площадь фигуры равна (см. рисунок).

11

		φ2
	S = 12 φ∫(ρ22 (φ) − ρ12 (φ))dφ .
		1
	Пример 2.			Найти площадь фигуры,
	ограниченной линией, заданной в по-
	лярной системе координат уравнением
	ρ =3 +sinφ .
	Решение
			π
		1	2		2		π
							2
	S = 2		∫ (3 + sinφ)			dφ =(9φ − 6 cosφ )		π	+
		2					−
			π					2
			− 2

π
+ ∫2	1 −cos 2φdφ =9π +		1	π =9,5π .
−π	2		2
2
Пример 3.		Найти площадь фи-

гуры, ограниченной линиями, заданными в полярной системе ко-

ординат ρ = 2(1−cosφ); ρ = 2 .

Решение. Фигура, площадь которой требуется найти, показана на рисунке. Найдем точки пересечения окружности и кардиоиды.

Решая совместно данные уравнения, получим точки																								2;	π					2; −				π
																							A		2	,	B							2	.
		Вычислим площадь половины фигуры, которая в свою очередь делится на
части S1 и S2							(см. чертеж).
								π														π
1	S = S + S				=		1	2			2	dφ +			1 π	(2)		2	dφ =	1	4	2					1	+		1		cos 2φ)dφ +
				2				(2(1−cosφ))														(1− 2cosφ +
2			1				2	∫0							2 π∫					2 ∫0							2 2
															2
	1	π				3			1					π				π		3π						π					5
+		4	dφ =	2(			φ	−2sinφ +		sin 2φ)				2 +		2φ		π	= 2(			− 2) + 2(π −					)	=					π −		4 .
	2	π∫				2			4					0				2		4						2					2
		2																					Ответ: S =5π −8.

3. ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ ПЛОСКОЙ КРИВОЙ

Длина отрезка прямой, координаты точек концов которого известны, находится по формуле

LAB = (xB − xA )2 +( yB − yA )2 .

12

Поставим задачу: определить длину дуги плоской кривой, являющейся графиком функции y = f (x) и ограниченной точками (a, f (a)) и (b, f (b)). Для

этого разобьем плоскую кривую произвольными точками на n частей. Соединим полученные точки хордами. Длина полученной ломаной будет тем ближе

к длине дуги, чем больше n. Длина i-го звена ломаной равна ( xi )2 +( yi )2 , а длина всей ломаной равна сумме всех длин звеньев

n	( xi )	2	+(	yi )	2	n	(	y )2		( xi ) . Переходя к пределу при n →∞ и
Ln = ∑						= ∑ 1+	(	i	2
i=1						i=1		xi )
при условии, что max						xi →0	(или используя теорему Лагранжа), получим

формулу для вычисления длины дуги кривой:

b
L = ∫	′	2	dx.
	1+( f (x))
a
Если кривая задана параметрическими уравнениями x =ϕ(t),				α ≤ t ≤ β, где
			y =ψ(t)

ϕ(t) и ψ(t) и их производные непрерывны, а границы изменения параметра оп-

ределяют границы дуги, то длина кривой вычисляется по формуле

β

L = ∫ [ϕ′(t)]2 +[ψ′(t)]2 dt .

α

Пример 4.

Найти длину кривой y = ln(2x)

где

3 ≤ x ≤

8 .

Решение

1+ x2

′

2

1

′

2

1

f (x) =

= x

; 1+[ f (x)]

=1

+

=

x2

;

2x

x2

L = ∫

1+ x

dx =

t = 1+ x

2

; x =

t

2

−1; dx =

tdt

= ∫

t2

dt =

t

2 −1

8

2

3

2

3

x

x = 3

t = 2;

x =

8 t = 3

2

t

−1

= ∫3 (1+

1

)dt = (t +

1 ln

t −1

)

32 =

1+

1 ln

3 .

2

t

−1

2

t +1

2

2

2

x = a(t −sin t),

0 ≤ t ≤ 2π (первая арка

Пример 5. Найти длину кривой

= a(1−cost),

циклоиды).

y

Решение

yt′ = asin t; [xt′]2 +[yt′]2 = a2 (1−2cost +cos2 t +sin2 t) = 2a2 (1−cost) .

xt′ = a(1−cost);

Тогда

2π

L =

2∫π a

2(1−cost)dt =

2∫π a

4sin

2

t

dt = 2a

2∫π sin

t

dt = −4a cos

t

=8a.

0

0

2

0

2

2

0

Пусть теперь кривая задана уравнением ρ = ρ(φ) в полярной системе координат и угол φ , отсчитываемый от полярной оси до радиус-вектора пере-

13

менной точки дуги кривой, меняется в пределах (φ1 ≤φ ≤φ2 ) . Тогда при усло-

′

длина кривой вы-

вии непрерывности функции ρ(φ) и ее производной ρ (φ)

числяется по формуле

φ2

′

2

2

L = ∫ [ρ(φ)]

+[ρ (φ)] dφ .

φ1

Пример 6. Найти длину кривой ρ = a(1−cosφ)

0 ≤φ ≤ 2π,

(кардиоида).

Решение. Данная кривая симметрична относительно полярной оси. Найдем

половину длины кардиоиды.

1 L = π∫

a2 (1−cosφ)2 + a2 (sinφ)2 dφ =aπ∫

1−2 cosφ +cos2 φ +sin2 φdφ =

2

0

0

π

π

π

2 2 sin

2 φ

π

φ

φ

= a∫

2 −2cosφdφ =a∫

2(1−cosφ)dφ = a∫

dφ =4a∫sin

d

=

0

0

0

2

0

2

2

φ

π

π

= 4a(−cos

)

= 4a(−cos

+cos 0) = 4a.

2

0

2

Длина кардиоиды равна L =8a .

4. ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА

Пусть имеется тело, площади параллельных сечений которого заданы как некоторая функция S(x) , в каждой точке x [a,b]. В этом случае объем тела

равен V = ∫b S(x)dx , так как задача сводится к построению интегральной суммы

a

n

∑S(ci ) xi ; ci [xi−1; xi ].

i=1

Рассмотрим важный случай, когда требуется найти объем тела вращения. Найдем объем тела, об-

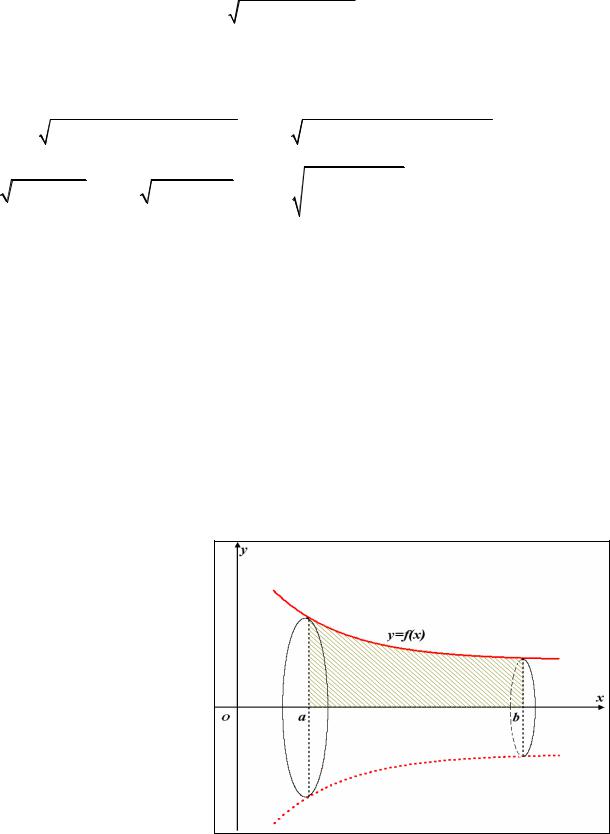
разованного вращением вокруг оси Ox криволинейной трапеции, ограниченной графиком непрерывной функции y = f (x) и прямыми x = a, x = b, y = 0. Очевидно,

что в этом случае поперечное сечение при любом значении x [a,b], S(x) =πR2 (x) =π f 2 (x)

Тогда получим

V =π∫b y2 (x)dx.

a

Если плоская фигура, ог-

раниченная линиями x = x( y), y = c, y = d, x = 0, вращается вокруг оси Oy , то соответствующая формула имеет вид

14

V =π∫d x2 ( y)dy.

c

Пример 6. Найти объем тела (тора), полученного при вращении вокруг оси абсцисс плоской фигуры, ограниченной линией x2 +(y −3)2 = 4 .

Решение. Плоская фигура ограничена сверху кривой y = 3 +					4 − x2	, а снизу
			1
	y2 =3 −		4 − x2 , тогда
		x2		x2
	V =π ∫( y1(x))2 dx −π ∫( y2 (x))2 dx =
		x1		x1
	=π ∫2	[(3 + 4 − x2 )2 −(3 − 4 − x2 )2 ]dx =
	−2
		2		x = 2sin t;	x = −2 t = −		π
	=12π ∫		4 − x2 dx =				2	=
		−2		dx = 2costdt; x = 2 t =			π
							2
		π			π
	=12π ∫2		4 −4sin2 t 2costdt = 48π ∫2			1+cos 2tdt =
		−π			−π	2
		2			2

= 24π2.

Пример 7. Найти объем тела, полученного при вращении вокруг оси орди-

нат плоской фигуры, ограниченной линией x2 + y2 =1 (эллипсоид вращения). a2 b2

Решение

y2

b

2

3

V =π ∫x2dy =π ∫a2 (1−

y

)dy = 2πa2

( y −

y

)

b0

=

4

πa2b .

2

3b

2

3

y1

−b

b

Приближенное вычисление определенного интеграла

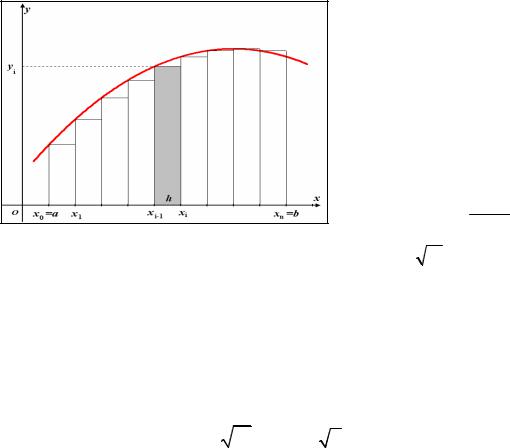
В основе приближенного вычисления определенного интеграла лежит построение интегральной суммы и тот факт, что данная сумма приближенно равна интегралу, и тем точнее, чем больше n. Рассмотрим простейший из численных методов − метод прямоугольников.

Разобьем интервал интегрирования [a,b] на n равных интервалов точками

15

( y1 + y2 + y3 +... + yn ) .

a = x , x , x ,..., x		n−1	, x = b , так,	что	x − x	= h =	b −a	;	(i =1, 2,...., n)	и найдем зна-
0 1	2		n		i i−1		n
чения	подынтегральной				функции		в		точках	разбиения:
y0 = f (x0 ),	y1 = f (x1 ),..., yn = f (xn ).			Построим ступенчатую фигуру, выбирая точки

xi на правых концах интервалов разбиения.

Площадь ступенчатой фигуры и, следовательно, приближенное значение определенного интеграла, равно

≈ b −a I1 n

Построим ступенчатую фигуру другим способом. Выбирая точки на левых концах интервалов, найдем площадь фигуры по формуле

I2 ≈ b −n a ( y0 + y1 +... + yn−1) .

За приближенное значение определенного интеграла обычно принима-

ют значение I ≈ I1 +2 I2 .

Пример. Найти точное значение интеграла ∫2 x3 dx по формуле Ньютона-

1

Лейбница. По формулам прямоугольников найти его приближенное значение. Вычислить абсолютную и относительную погрешность приближенного значения. В расчетах использовать разбиение отрезка интегрирования на 10 равных частей. Промежуточные вычисления вести, сохраняя три знака после запятой.

Решение. Вычислим данный интеграл сначала по формуле НьютонаЛейбница. Получим

					∫2	x3 dx = 2 (4			2 −1) =1,862 .
				1			5
Вычислим значения подынтегральной функции в точках разбиения. Резуль-
таты сведем в таблицу.
x	1	1,1	1,2	1,3			1,4		1,5	1,6	1,7		1,8	1,9	2,0
f (x)	1	1,154	1,315	1,482			1,657		1,837	2,024	2,217		2,415	2.619	2,828
												10
По первой формуле прямоугольников получим I1 = 0,1 ∑yk =1,954 .
												k =1
							9
Вторая формула дает I2						= 0,1 ∑yk =1,772 .					За приближенное значение
					I1 + I2		k =0
интеграла можно взять							=1,863 . Найдем абсолютную погрешность вы-
						2

16

числения	=		1,863 −1,862				= 0,001. Относительная погрешность равна
δ = I 100% =	0,001			100%	= 0,054% .
	1,863

Библиографический список

1.Пискунов Н. С. Дифференциальное и интегральное исчисление: В 2 т. Т.2.: учеб. для втузов: − М. : Интеграл-Пресс, 2001.

2.Письменный Д. Т. Конспект лекций по высшей математике: полный курс.− М. : Айрис-пресс, 2004.

3.Берман Г. Н. Сборник задач по курсу математического анализа.− СПб. : Изд-

во «Лань», 2000.

4.Лунгу К. Н., Письменный Д. Т., Федин С. Н., Шевченко Ю. А. Сборник задач по высшей математике: 1 курс. − М. : Айрис-пресс, 2004.

17

Индивидуальные задания

Вариант 1

1. Вычислить несобственный интеграл или доказать его расходимость

						∞
						∫1	dx	.
							x(x +1)
2. Найти площадь фигуры, ограниченной линиями
	y = x2 ; 4 y = x2 ;		x = 2;	x = −2. Построить чертеж.
3.	Найти площадь фигуры, ограниченной линией, заданной в полярной сис-
теме координат ρ = a cos3φ .
4.	Найти длину дуги кривой					y2 = x3 на промежутке от точки О(0; 0) до
точки А(4; 8) .
5.	Найти объем тела, полученного вращением вокруг оси Ох фигуры, огра-
ниченной линиями y =			1		;	x =1; x = −1; y = 0 . Построить чертеж.
			1 + x2
6. Интеграл ∫3		(x +1)3 dx вычислить точно по формуле Ньютона-Лейбница и
	1

приближенно по формуле прямоугольников. Отрезок интегрирования разбить на 10 частей. Все вычисления проводить, сохраняя четыре знака после запятой. Приближенное значение интеграла округлить до третьего десятичного знака. Найти абсолютную и относительную погрешность результата вычислений.

Вариант 2

1. Вычислить несобственный интеграл или доказать его расходимость

∞ ln x

∫1 x2 dx .

2.Найти площадь фигуры, ограниченной линиями y2 = 4 + x; x +3y = 0. Построить чертеж.

3.Найти площадь фигуры, ограниченной линией, заданной в полярной сис-

теме координат ρ = 2 +cosφ .	π .
4. Найти длину дуги кривой y = ln cos x на промежутке 0 ≤ x ≤
	4

5. Найти объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями y = −x2 ; x + y + 2 = 0 . Построить чертеж.

5	( x12 +3x2 )dx вычислить точно по формуле Ньютона-Лейбница
6. Интеграл ∫2

и приближенно по формуле прямоугольников. Отрезок интегрирования разбить на 10 частей. Все вычисления проводить, сохраняя четыре знака после запятой. Приближенное значение интеграла округлить до третьего десятичного знака. Найти абсолютную и относительную погрешность результата вычислений.

18

Вариант 3

1. Вычислить несобственный интеграл или доказать его расходимость

				∞∫x e−2 xdx .
			0
	2.	Найти площадь фигуры, ограниченной линиями xy = 4; y = x; x = 4. По-
	строить чертеж.
	3.	Найти площадь фигуры, ограниченной линией, заданной в полярной сис-
	теме координат		ρ = 2(1−cosφ) .
	4. Найти длину дуги кривой y = ln					1	на промежутке	0 ≤ x ≤ π .
						cos x
								3
	5.	Найти объем тела, полученного вращением вокруг оси Ох фигуры, огра-
	ниченной линиями y =sin x; y =			2	x . Построить чертеж.
				π
	6. Интеграл ∫8		(x −2)3 dx вычислить точно по формуле Ньютона-Лейбница и
		2

приближенно по формуле прямоугольников. Отрезок интегрирования разбить на 10 частей. Все вычисления проводить, сохраняя четыре знака после запятой. Приближенное значение интеграла округлить до третьего десятичного знака. Найти абсолютную и относительную погрешность результата вычислений.

Вариант 4

1. Вычислить несобственный интеграл или доказать его расходимость

∞∫x e−x2 dx .

0

2. Найти площадь фигуры, ограниченной линиями y2 = x; 4x = y2 ; y = 2; y = −2. Построить чертеж.

3. Найти площадь фигуры, ограниченной линиями, заданными в полярной

системе координат ρcosφ =5;	ρ =10 (взять фигуру с меньшей площадью).
4. Найти длину дуги кривой	x = 2sin2 t;	на промежутке 0 ≤t ≤	π .
	y =sin 2t		2

5. Найти объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линией y =sin x; 0 ≤ x ≤π . Построить чертеж.

4	x3 + 2
6. Интеграл ∫			dx	вычислить точно по формуле Ньютона-Лейбница и
	x	5
1

приближенно по формуле прямоугольников. Отрезок интегрирования разбить на 10 частей. Все вычисления проводить, сохраняя четыре знака после запятой. Приближенное значение интеграла округлить до третьего десятичного знака. Найти абсолютную и относительную погрешность результата вычислений.

19