umm_1943

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения

Кафедра «Высшая математика»

Э. Е. Поповский П. П. Скачков

ОПРЕДЕЛЕННЫЙ

ИНТЕГРАЛ

Екатеринбург

2009

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения

Кафедра «Высшая математика»

Э. Е. Поповский П. П. Скачков

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Типовой расчет

Методические указания по выполнению типового расчета для студентов всех специальностей

Екатеринбург

2009

1

УДК 517.38 П 58

Поповский Э. Е., Скачков П. П.

Определенный интеграл. Типовой расчет. Методические указания по выполнению типового расчета для студентов всех специальностей. − Екатеринбург:

УрГУПС. 2009.− 32 с.

Первая часть работы содержит краткие теоретические сведения, необходимые для решения задач типового расчета. Рассмотрены примеры для всех типов заданий. При этом приведены подробные решения наиболее важных типов задач с необходимыми пояснениями и ссылками на теоретический материал.

Вторая часть указаний представляет собой индивидуальные задания. По уровню сложности и тематике они носят характер, соответствующий требованиям программы по математике для технических вузов.

Одобрено и рекомендовано к изданию на заседании кафедры высшей математики УрГУПС (протокол № 1 от 11.02.2009 г.).

Авторы: Э. Е. Поповский, доцент кафедры «Высшая математика», УрГУПС П. П. Скачков, доцент кафедры «Высшая математика», канд. физ.-мат. наук, УрГУПС

Рецензент: Г. А. Тимофеева, зав. кафедрой «Высшая математика», д-р физ.-мат. наук, профессор, УрГУПС

© Уральский государственный университет путей сообщения (УрГУПС), 2009

2

ОГЛАВЛЕНИЕ
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ (элементы теории) ……………………. 4
Определение определенного интеграла. Задача о площади
криволинейной трапеции ……………………………………………………. 4
Свойства определенного интеграла ………………………………………… 5
Формула Ньютона-Лейбница ……………………………………………….. 6
Замена переменной и интегрирование по частям в определенном
интеграле ………………………………………………………………………7
Несобственные интегралы ………………………………………………….. 8
1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ ...............................................................	8
2. ИНТЕГРАЛЫ ОТ ФУНКЦИЙ, ИМЕЮЩИХ РАЗРЫВ ВТОРОГО РОДА ………………………… 9
Геометрические приложения определенного интеграла …………………..10
1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР В ДЕКАРТОВОЙ СИСТЕМЕ
КООРДИНАТ .........................................................................................................	10
2. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР В ПОЛЯРНОЙ СИСТЕМЕ

КООРДИНАТ ……………………………………………………………………. 11

3.ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ ПЛОСКОЙ КРИВОЙ ………………………………………. 12

4.ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА ………………………………………………………14

Приближенное вычисление определенного интеграла ……………………15

Библиографический список …………………………………………………17

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ……………………………………….18

3

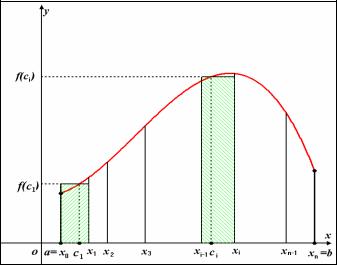
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ (элементы теории)

Определение определенного интеграла. Задача о площади криволинейной трапеции.

Рассмотрим фигуру, ограниченную осьюOx , прямыми x = a, x =b и графиком функции y = f (x) , причем f (x) ≥ 0 на [a,b]. Такая фигура называется кри-

волинейной трапецией. Найдем площадь этой фигуры.						Для этого разобьем
отрезок	[a,b]	произвольным	образом	на	n	частей		точками
a = x0 < x1 < x2 <... < xn =b с длинами частичных					отрезков		x1 = x1 − x0 ,
x2 = x2 − x1 ,...,		xn = xn − xn−1 , или	xi = xi − xi−1		(i =1, 2,..., n) . Выберем на
каждом из этих отрезков произвольным способом точку ci [xi−1, xi ]								и найдем
значение функции		в этой точке f (ci ) . Проведем через точки с координатами
(ci , f (ci ))	горизонтальные отрезки длиной xi . Выполнив данное построение,

получим ступенчатую фигуру. На рисунке для простоты построено только два

прямоугольника с основаниями xi , высотами f (ci ) Площадь всей ступенчатой фигуры очевидно равна.

n

Sn = f (c1 ) x1 + f (c2 ) x2 +... + f (cn ) xn = ∑

i=1

Сумма, построенная по изложенным правилам, называется инте-

гральной суммой.

Из рисунка видно, что площадь ступенчатой фигуры, равная интегральной сумме, не равна площади криволинейной трапеции. Однако, легко предположить, что при увеличении числа разбиений n и одновременном уменьшении длин интервалов раз-

биения Sn будет неограниченно приближаться к площади криволинейной трапеции S. Таким образом, площадь

и площадями f (ci ) xi .

f (ci ) xi

криволинейной трапеции равна S = nlim→∞			n
			∑ f (ci ) xi .
max(	x	)→0	i=1
Определение. Пусть на отрезке [a,b]	i	задана функция y = f (x) . Разобьем

отрезок на n частей произвольным образом точками a = x0 < x1 <... < xn = b . На каждом отрезке [xi−1, xi ], длиной xi = xi − xi−1 , выберем произвольно точку

n

ci [xi−1, xi ] и составим интегральную сумму ∑ f (ci ) xi . Если существует пре-

i=1

4

дел интегральной суммы при n → ∞ и λ = max( xi ) → 0 , который не зависит ни от способа разбиения отрезка [a,b] на частичные отрезки, ни от выбора точек ci [xi−1, xi ] , то этот предел называется определенным интегралом от функции y = f (x) на отрезке [a,b] и обозначается так:

	n	b
limn→∞	∑ f (ci )	xi = ∫ f (x)dx .
λ→0	i=1	a

Числа a и b называются соответственно нижним и верхним пределами ин-

тегрирования; х − переменной интегрирования. Заметим, что определенный интеграл − это число.

Теорема. Если функция y = f (x)	непрерывна на отрезке [a,b], то опреде-
ленный интеграл существует и конечен.
Замечание. Если функция f (x) ≥ 0	на промежутке [a,b], то ∫b	f (x)dx равен
	a

площади соответствующей криволинейной трапеции.

Свойства определенного интеграла

1. Постоянный множитель можно выносить за знак интеграла

∫b kf (x)dx = k ∫b		f (x)dx, (k = const).
a	a

2. Интеграл от суммы функций равен сумме интегралов от этих функций

∫b ( f (x) + g(x))dx = ∫b		f (x)dx + ∫b g(x)dx .
a	a	a

3. Если верхний и нижний пределы интегрирования поменять местами, то интеграл меняет свой знак

∫b	f (x)dx = −∫a	f (x)dx .
a	b

4. Величина определенного интеграла не зависит от переменной интегрирования

∫b	f (x)dx = ∫b	f (t)dt .
a	a

5. Если верхний и нижний пределы интегрирования равны, то определенный интеграл равен нулю

∫a f (x)dx = 0.

a

6. Интеграл на отрезке [a,b] равен сумме интегралов

5

∫b	f (x)dx = ∫c	f (x)dx + ∫b	f (x)dx .
a	a	c

При этом точка с может лежать как внутри отрезка [a,b], так и вне его, если

все указанные интегралы существуют.

7. Если подынтегральная функция равна единице, то интеграл численно равен длине отрезка интегрирования (b −a) .

		∫b	1 dx = b −a.
		a
8. Если	некоторые функции f (x) и g(x) удовлетворяют условию
f (x) ≥ g(x),	x [a,b], то и интегралы от этих функций удовлетворяют этому
же условию	∫b	f (x)dx ≥ ∫b g(x)dx .
	a		a

9. Теорема об оценке интеграла. Если подынтегральная функция y = f (x) имеет на отрезке [a,b] наибольшее значение, равное М, и наименьшее значе-

ние, равное m, то

m(b −a) ≤ ∫b f (x)dx ≤ M (b −a).

a

10. Теорема о среднем значении. Если функция y = f (x) непрерывна на отрезке [a,b], то существует такая точка c [a,b], что

∫b	f (x)dx = f (c) (b −a).
a

Формула Ньютона-Лейбница

Теорема. Если F (x) какая-либо первообразная функции f (x) , то справедлива формула

b

∫ f (x)dx = F (x) ba = F (b) − F (a).

a

Эта формула устанавливает связь между неопределенным и определенным интегралами и носит название формулы Ньютона-Лейбница. Формула дает удобный способ вычисления определенного интеграла.

Пример 1. Вычислить интеграл ∫b xndx.

a

Решение	∫b xndx =	xn+1			b	= bn+1 −an+1				(n ≠ −1).
	a	n +1			a	n +1
						2			x		dx.
Пример 2. Вычислить интеграл ∫
								x2	+4
						1

6

2	x		1	2	d (x2 +4)		1	2		2		1			ln1,6
Решение ∫1		dx =	2	∫1	x2 +4	=	2 ln (x		+4)		=	2	(ln 8 −ln 5)	=	2	.
	x2 +4									1

Замена переменной и интегрирование по частям в определенном интеграле

Замена переменной проводится в случае, если получаемый интеграл вычисляется проще, чем исходный и выполняется в двух вариантах.

b		x =ϕ(t);	ϕ(α) = a; t =α			β			β
а) ∫	f (x)dx =						′		= F(β) − F(α).
		′				=∫ f (ϕ(t))ϕ (t)dt = F (t)
a						α			α
		dx =ϕ (t)dt; ϕ(β) = b; t = β
Данный интеграл существует, если функции							f (x), ϕ(t), ϕ (t) непрерывны.
							′
b		′		′			B
				u =ϕ(x); du =ϕ	(x)dx		= ∫ f (u)du = F(B) − F ( A).
б) ∫ f (ϕ(x))ϕ (x)dx =				ϕ(a) = A; ϕ(b) = B
a							A

Замечание. При вычислении определенного интеграла методом замены переменной нет необходимости возвращаться к старой переменной.

Пример 1. Вычислить интеграл							∫2	4 − x2 dx.
							0
			∫2		x = 2sin t; x = 0 t = 0										π
Решение				4 − x2 dx =							π			= ∫2
			0		dx = 2costdt; x = 2 t =						2				0
π				π		π
2		2		2	2	2	1		1			t
= 4∫	1−sin		t costdt = 4∫cos			tdt =4∫		+		cos 2t dt =4					+
									2					2
0				0		0	2

π

4 −4sin2 t 2costdt =

π

sin 2t 2 =π 4 0 .

	Пример 2. Вычислить интеграл		∫2	3 sin5 x cos xdx.
	Решение		0
π
		u = sin x; u = sin 0 = 0							1			83		1
∫2											3 u				3 .
	3 sin5 x cos xdx =	du = cos xdx; u = sin			π	=1	= ∫3 u5 du =							=
0					2				0		8			0	8
	Пример 3. Вычислить интеграл		∫e			dx				.
				x	1−ln			2
			1						x

Решение

e	dx			e	d (ln x)			= arcsin (ln x)	e
∫				= ∫
		2				2
1	x 1−ln		x 1		1−ln		x	1

= arcsin(ln e) −arcsin(ln1) = arcsin1 = π2 .

Интегрирование по частям для определенного интеграла производится по формуле

7

b b

∫udv =u v ba −∫vdu .

a a

Пример 4. Вычислить интеграл

∫e

x ln xdx.

Решение

1

dx

e

u = ln x; du =

x2

e

e

x2

dx

x2

1

e

e2 +1

x

∫x ln xdx =

=

ln x

1

−∫

x

=

(ln x −

)

1

=

.

x

2

2

2

2

2

4

1

dv = xdx; v =

1

2

Несобственные интегралы

1. ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ

Определение. Пусть

определению

∞∫ a

функция f (x) определена и непрерывна при всех значениях x a, ∞). Несобствен-

ным интегралом с бесконечным верхним пределом называется предел следующего вида:

b

limb→∞ ∫a f (x)dx ,

который обозначается так:

∞∫ f (x)dx . Следовательно, по

a

b

f (x)dx = limb→∞ ∫a f (x)dx .

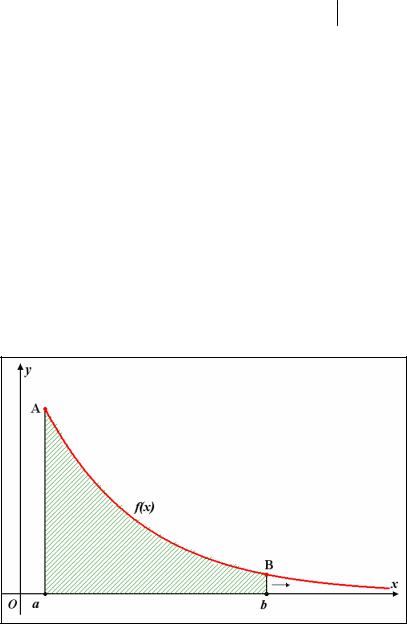
Если f (x) ≥ 0 , то в соответствии с геометрическим смыслом определенного интеграла он представляет собой площадь криволинейной трапеции с бесконечным основанием как показано на рисунке.

Если указанный предел существует и конечен, то говорят, что интеграл сходится, в этом случае криволинейная трапеция с бесконечным основанием имеет конечную площадь. Если же предел бесконечен или не существует, то говорят, что интеграл расходится.

Аналогично определяется интеграл с бесконечным нижним пределом

∫b	f (x)dx = alim→−∞ ∫b	f (x)dx.
−∞	a

8

Интегралы с бесконечными пределами интегрирования, а также интеграл

∞∫	f (x)dx = alim→−∞ ∫c	f (x)dx +limb→∞	∫b	f (x)dx , где с любая точка,
−∞	a		c

называются несобственными интегралами I-го рода. В последнем случае интеграл будет сходящимся, если сходятся оба интеграла, стоящие в правой части равенства.

Пример 1. Вычислить интеграл ∞∫

1

dx

или установить его расходи-

1+ x

2

мость.

a

b

∞

1

1

b

= π .

dx = lim

dx = lim arctg x

= lim(arctgb −arctg0)

Решение ∫

1+ x

2

b→∞ ∫

+ x

2

b→∞

0

b→∞

2

0

0 1

Данный интеграл сходится и его численное значение равно π .

Пример 2. Вычислить интеграл +∞∫

dx

2

или установить его расходимость.

1 1+ x

+∞

dx

dx = lim b

dx

= lim ln(1+ x)

b

= lim ( ln(1+b) −ln 2) = +∞.

Решение

∫

1+ x

b→+∞ ∫

1+ x

b→+∞

1

b→+∞

1

1

Таким образом, данный интеграл расходится.

2. ИНТЕГРАЛЫ ОТ ФУНКЦИЙ, ИМЕЮЩИХ РАЗРЫВ ВТОРОГО РОДА

Пусть функция y = f ( x) непрерывна на интервале x [a,b) и имеет разрыв

второго рода в точке b, тогда несобственным интегралом второго рода называется предел вида

b−ε

limε→0 ∫a f (x)dx , где ε > 0. Ес-

ли данный предел существует и конечен, то интеграл называют сходящимся, в противном случае − расходящимся. Следовательно, по определению

∫b	f (x)dx = limε→0 b∫−ε	f (x)dx .
a	a

Геометрическая иллюстрация приведена на рисунке

и означает, что если существует и сходится данный интеграл, то данная неограниченная криволинейная трапеция обладает конечной площадью. Если интеграл расходится, то и площадь трапеции бесконечна.

9