N=8 / N=8
.doc
Контрольная работа по математике 2012-13 уч. год, N=8.
1) Найти множество
,
если
.
Пересечение
Объединение
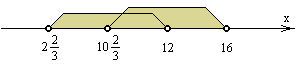
Разность
Ответ:
.
2) Докажите эквивалентность множеств
и
,
если
,
.
Если каждому элементу множества
можно по некоторому правилу поставить
в соответствие один и только один элемент
множества
и, наоборот, каждому элементу множества
можно по некоторому правилу поставить
в соответствие один и только один элемент
множества
,
то говорят, что между элементами множеств
и
установлено взаимно однозначное
соответствие. В этом случае множества
и
называют эквивалентными
и записывают
.
Установим, например, линейное
соответствие между данными промежутками
(соединим точки
и
прямой линией).
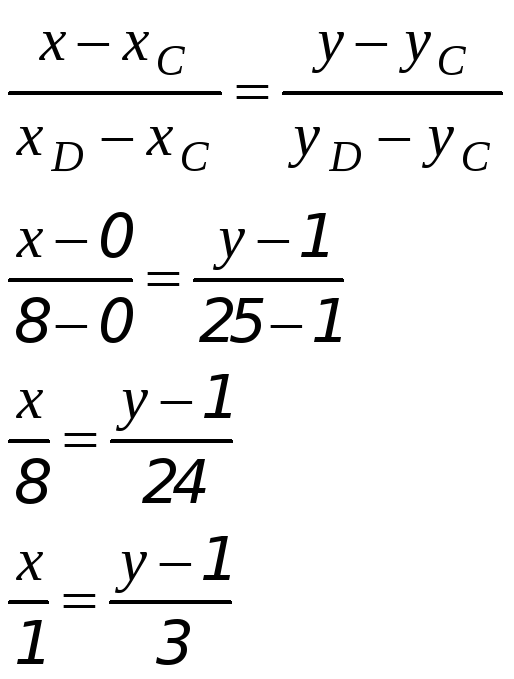
Если промежуток
изобразим в координатной плоскости на
оси абцисс, а промежуток
- на оси ординат, то между ними будет
взаимно однозначное соответствие,
описываемое например линейной зависимостью
.
Следовательно, соответствующие им
числовые множества эквивалентны:
.
3) Найдите:
а)
;
б)
.
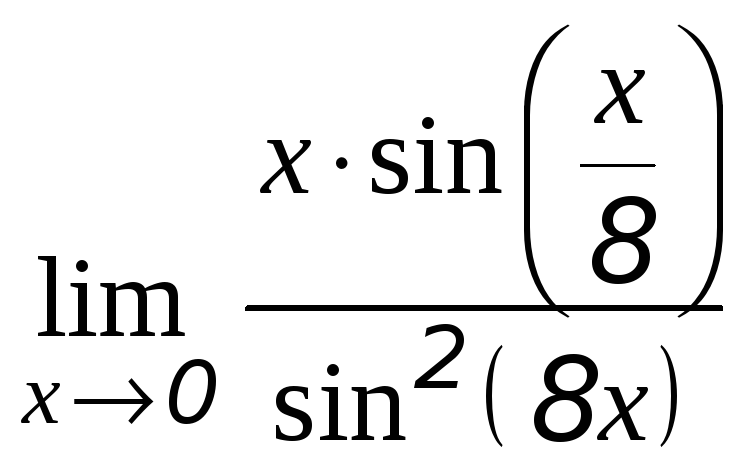а)
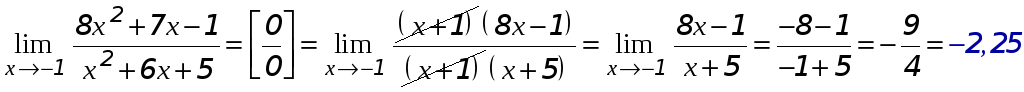
- неопределённость вида
устранена разложением числителя и
знаменателя алгебраической дроби на
множители с последующим сокращением
множителя, обуславливающего
неопределённость.
б)
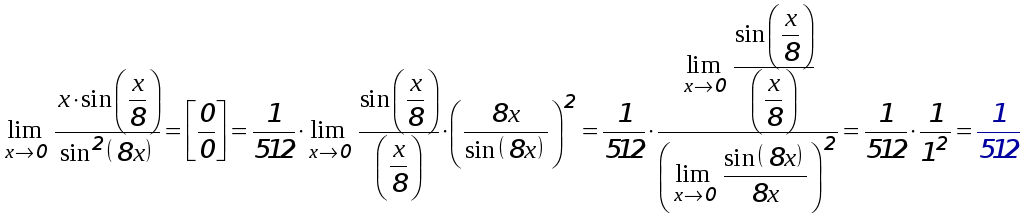
- неопределённость вида
устранена применением первого
замечательного предела.
4) Найдите производную функцию
.
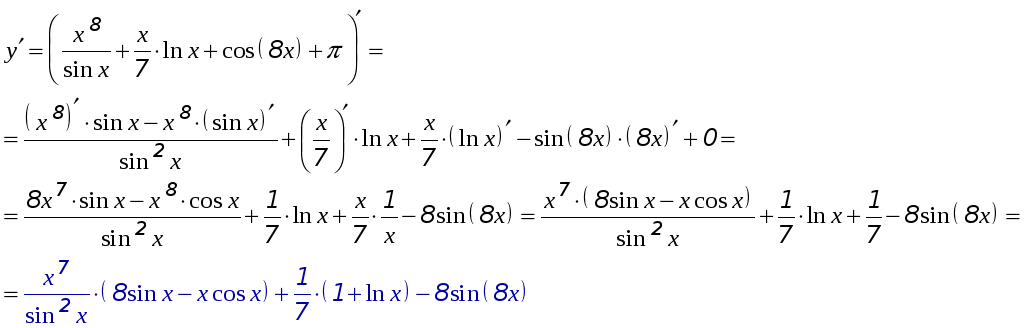
5) Найдите интервалы монотонности и
точки экстремума функции
.
Границами интервалов монотонности являются критические точки функции. Поэтому ищем критические точки. Критические точки - это точки, в которых производная функции равна нулю или не существует.
Область определения функции:
.
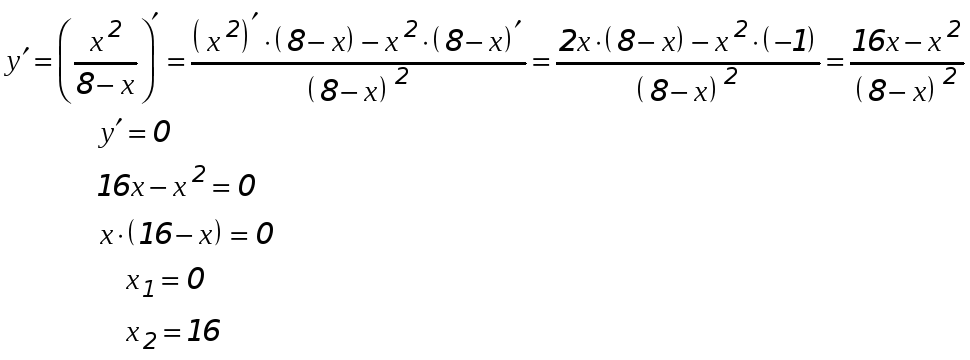
не существует при
.
Посмотрим на поведение функции в промежутках между критическими точками:
-
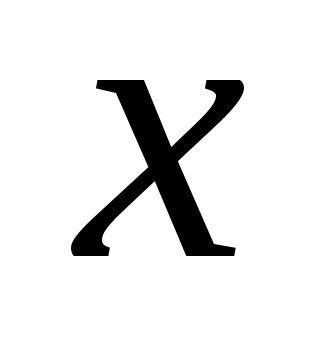
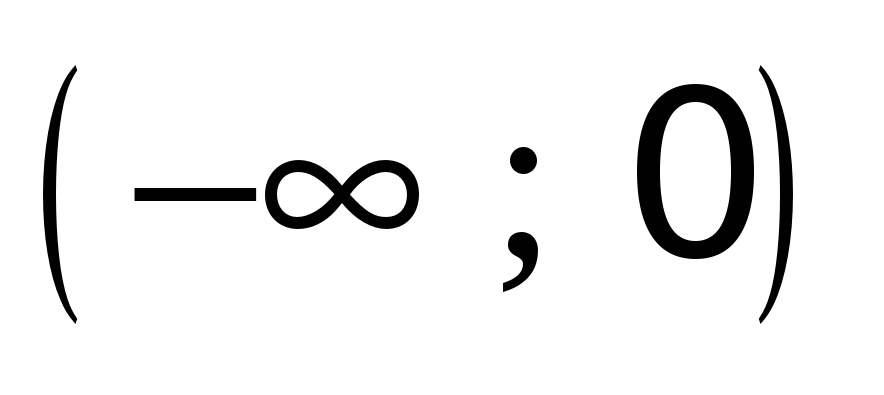
0
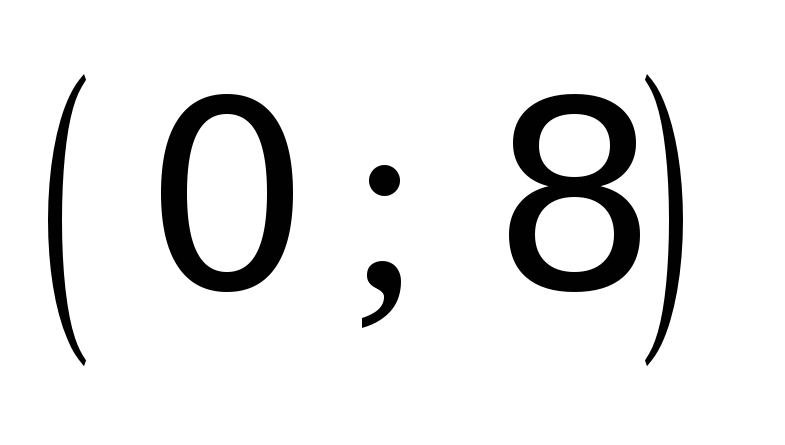
8
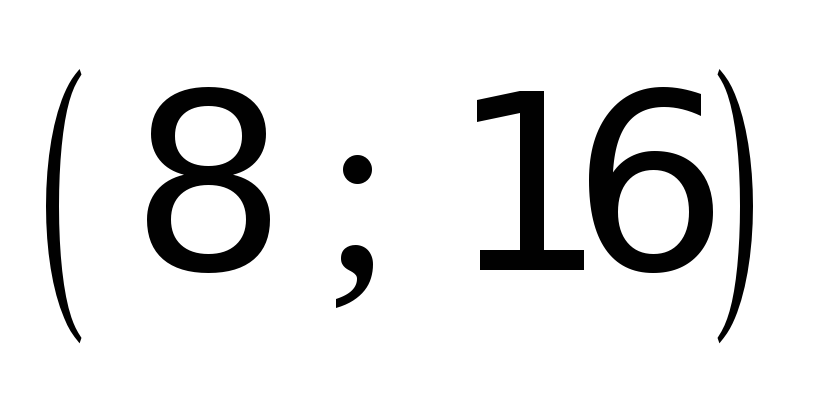
16
-
0
+
н.с.
+
0
-
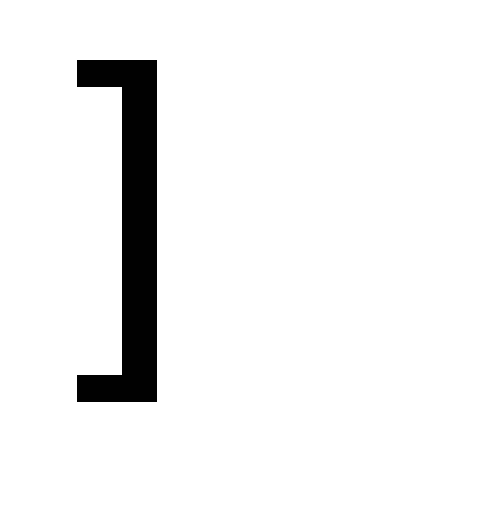
0
(min)
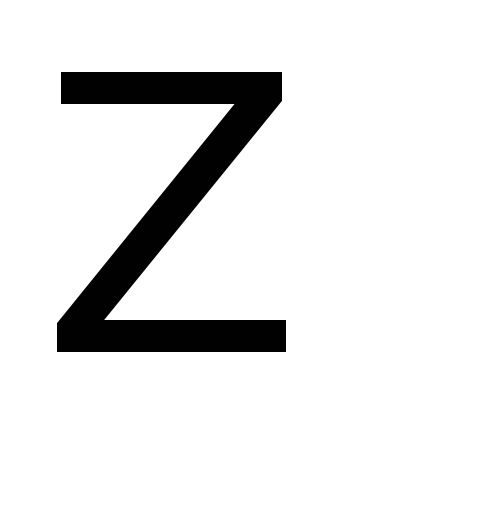
н.с.
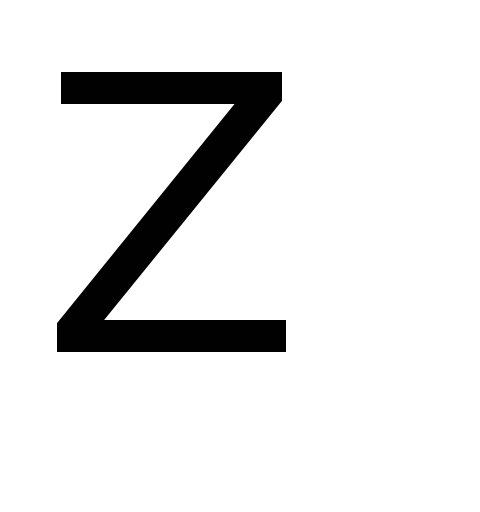
-36
(max)
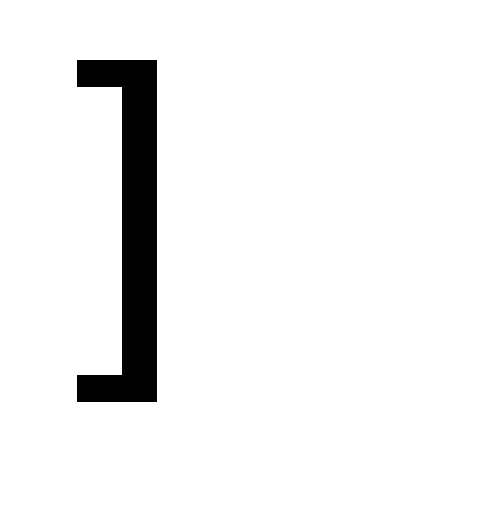
(н.с. - не существует;
- интервал убывания;
- интервал возрастания)
Функция монотонно убывает на промежутке
и монотонно возрастает на промежутке
.
Функция имеет минимум
и максимум
(точки экстремумов).
6) Найдите площадь фигуры, ограниченной
кривой
и осью
(
).
Эскиз фигуры:
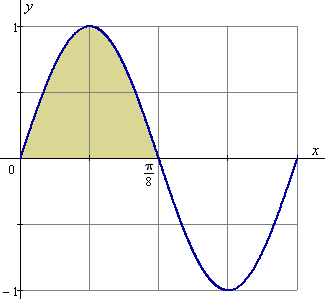
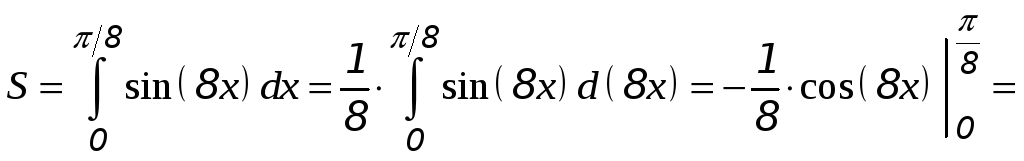
(кв. ед.)
7) Вычислите:
а)
;
б)
.
а)
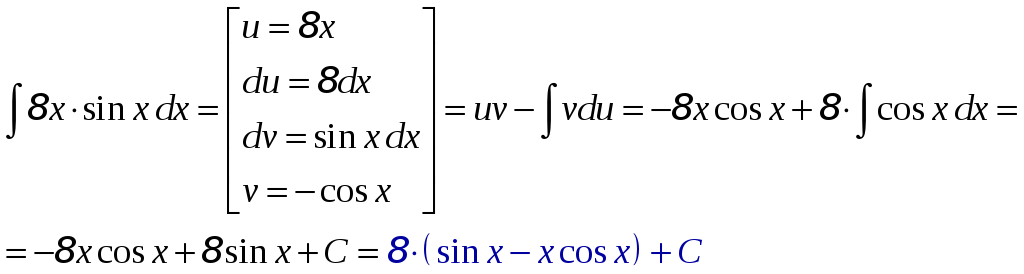
- применён метод интегрирования по частям.
б)
- применён метод подведения под знак дифференциала.
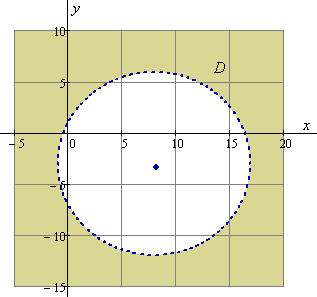
8) Найдите область определения функции
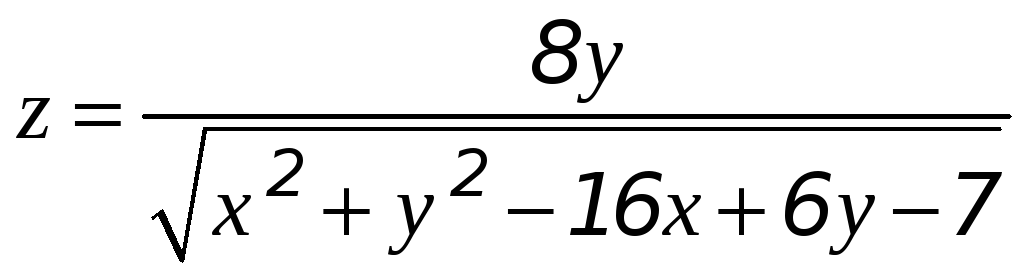
Область определения функции определяется условием
Выделим полные квадраты каждой переменной:
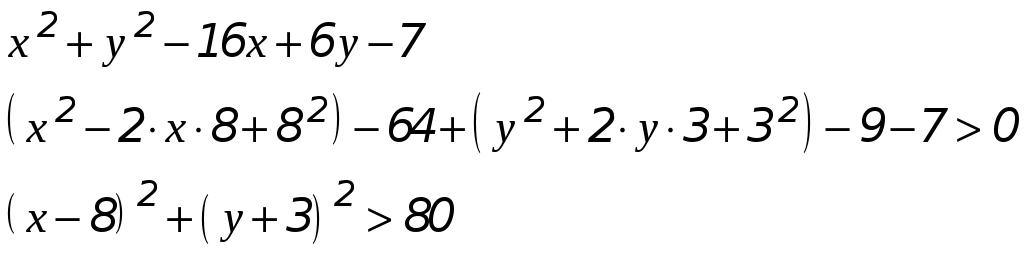
Геометрически область определения
функции
есть вся числовая плоскость, за исключением
круга с центром
и радиусом
:
.
9) Найти
и
,
где
.
Вычисляем первые производные функции
двух переменных
:
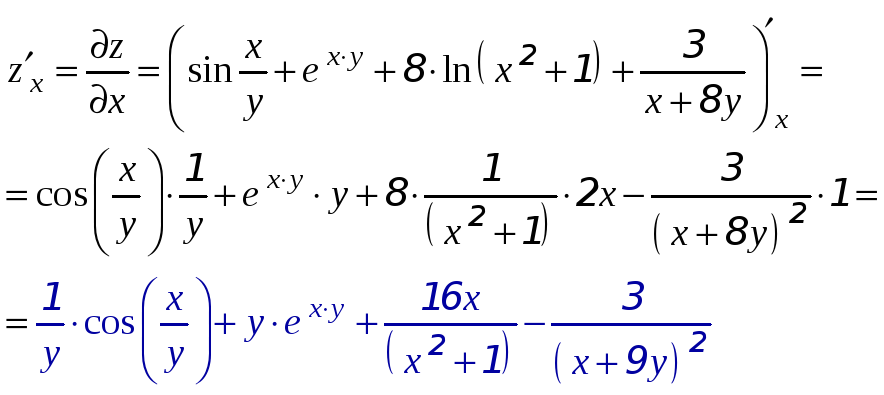
10) Найти точки экстремума функции
.
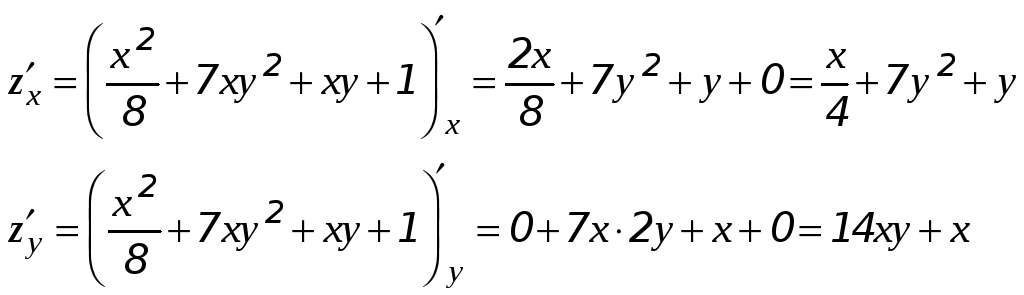
Находим стационарные точки:
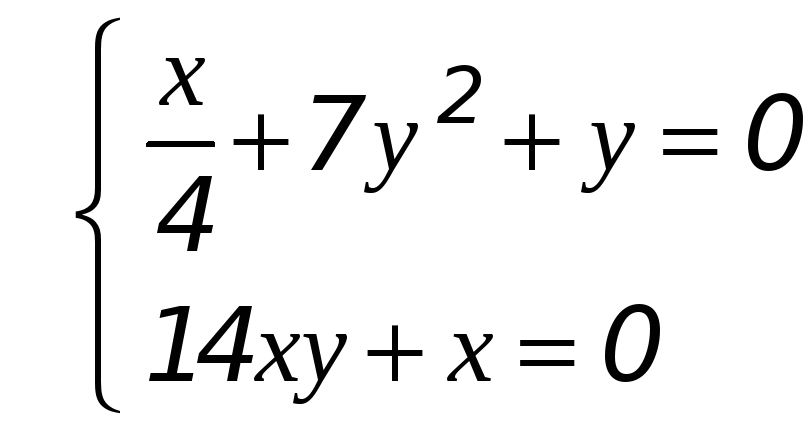
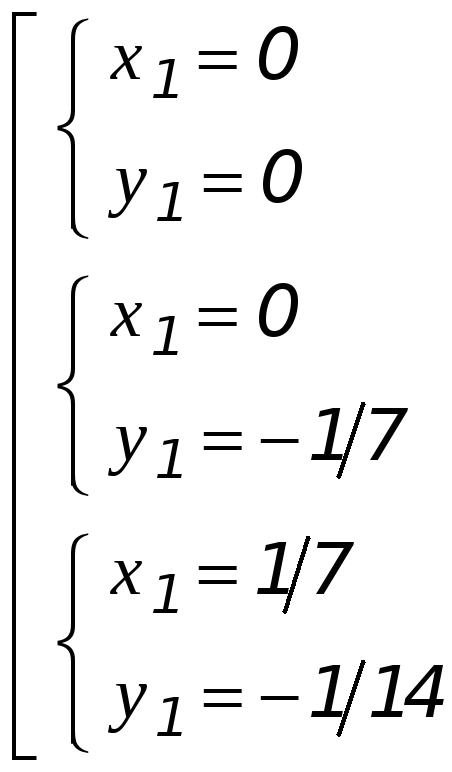
Найдены три стационарные точки
и
;
проверим их на соответствие достаточному
условию наличия экстремумов в данных
точках.
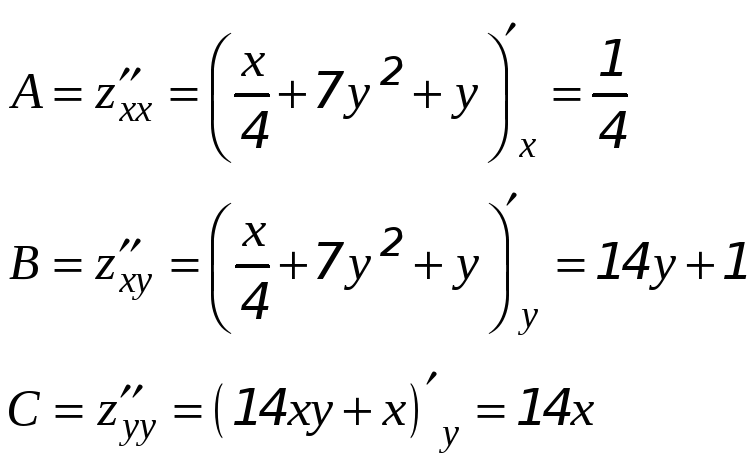
В точке
:
Поскольку
,
то в данной точке экстремума нет.
В точке
:
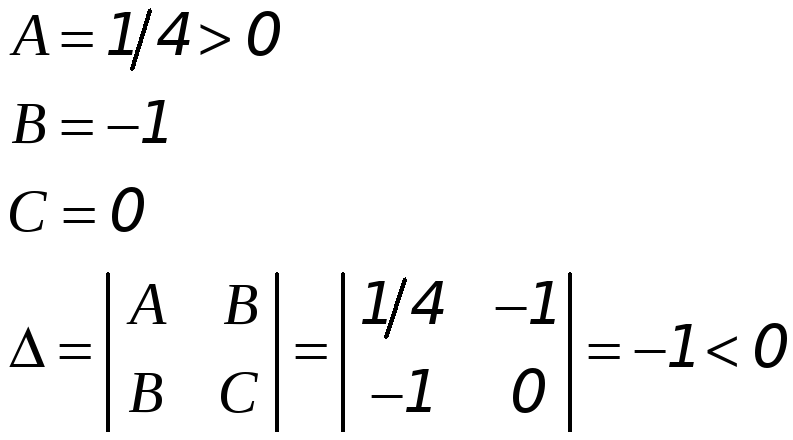
Поскольку
,
то в данной точке экстремума нет.
В точке
:
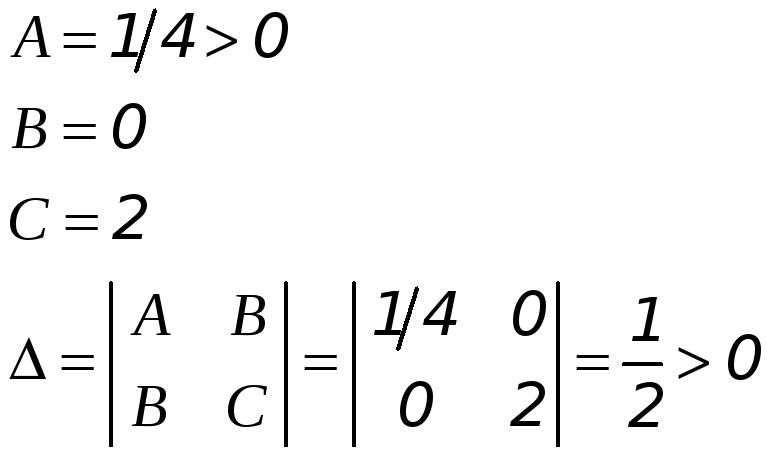
- в точке
минимум, т.к.
.
Значение функции в этой точке
.
Ответ: функция имеет локальный
минимум
.
11) Решить задачу Коши для дифференциального уравнения
.
- это линейное ДУ 1-го порядка
.
Его решение можно найти методом Бернулли
(замена
)
или методом Лагранжа (метод вариации
произвольной постоянной).
Используем для решения метод Бернулли.
Введём замену
,
тогда
:
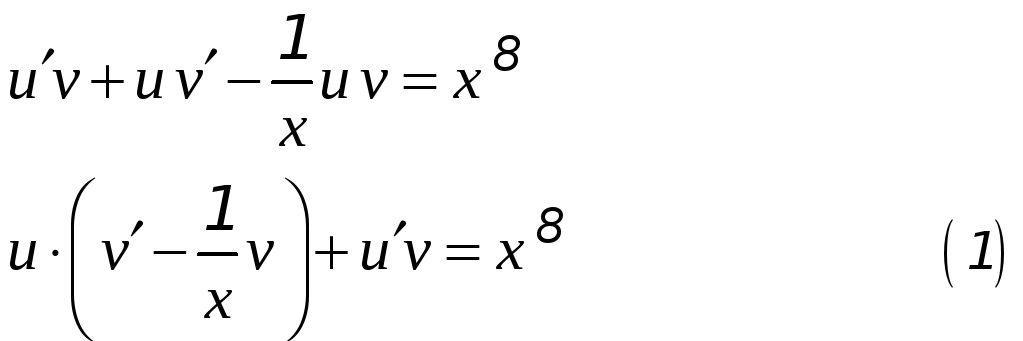
Выберем функцию
так, чтобы выражение в скобках обратилось
в ноль; т.е.
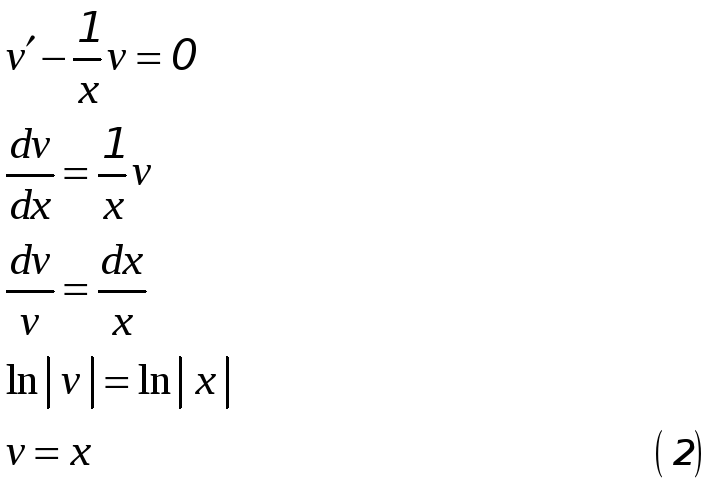
Перепишем (1) с учётом (2):
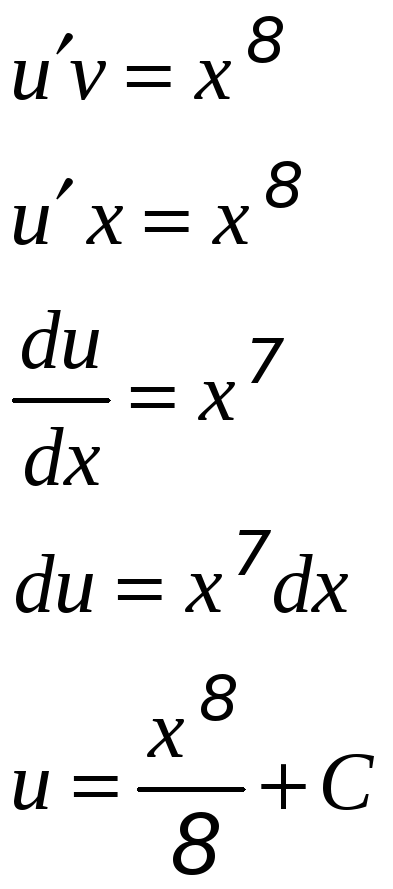
Возвращаясь к замене
,
получим:
- общее решение ДУ.
Используя начальные условия
,
находим константу
:
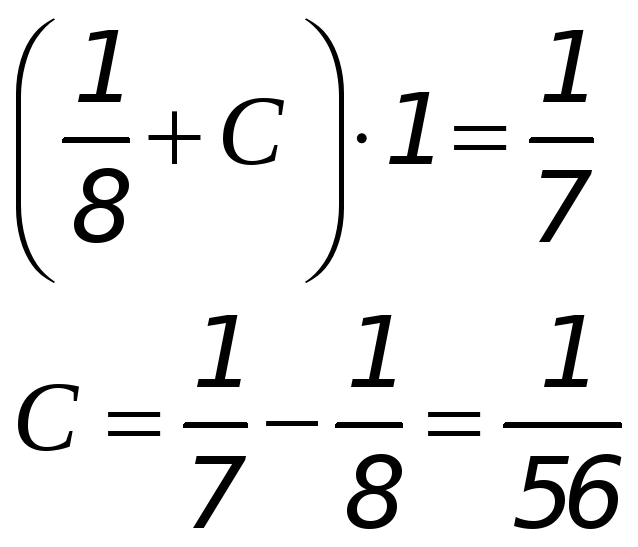
и
- частное решение ДУ, удовлетворяющее
заданным начальным условиям.
12) Найдите общее решение дифференциального уравнения
.
- линейное неоднородное ДУ 2-го порядка
с постоянными коэффициентами и правой
частью специального вида. Общее решение
уравнения представляет собой сумму
общего решения
соответствующего однородного уравнения
и частного решения
неоднородного уравнения:
.
► Сначала находим общее решение соответствующего однородного уравнения:
Характеристическое уравнение
имеет корни действительные
и различные
.
Следовательно, общее решение однородного
уравнения
► В случае, если правая
часть ДУ с постоянными коэффициентами
имеет специальный вид, частное решение
неоднородного уравнения может быть
найдено более простым способом: методом
неопределённых коэффициентов.
Правая часть ДУ имеет вид
поэтому частное решение ищем в виде
где 
– число, равное кратности
как корня характеристического уравнения,
- порядок многочлена
,
- многочлен степени
,
записанный с неопределёнными
коэффициентами,
т.е.
Тогда
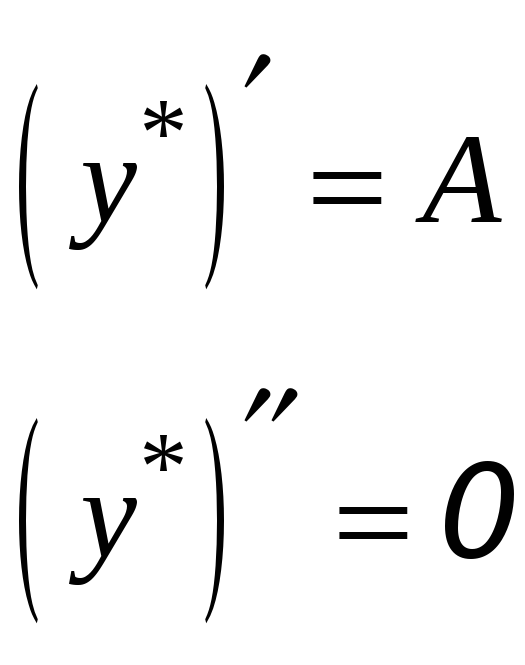
Подставив
,
,
в исходное уравнение, получим
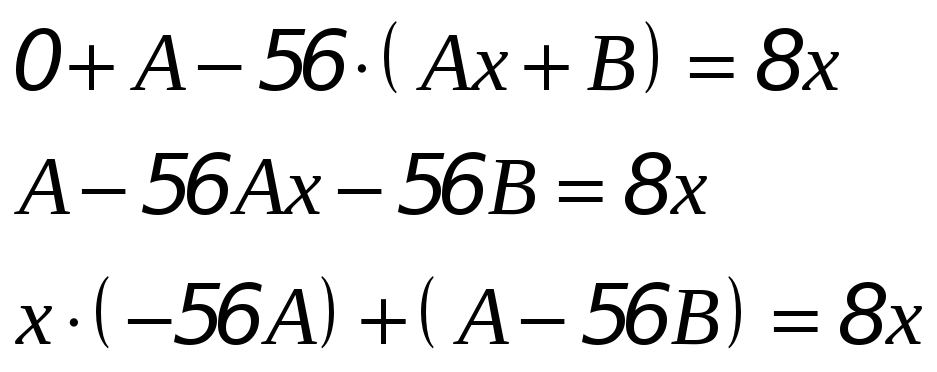
и вычислим
коэффициенты
и
:
Частное решение данного уравнения имеет вид
и, cледовательно, общее решение исходного уравнения имеет вид
