
M-031 / M-031, N=8
.doc
Контрольная работа M-031, часть 2, N=8.
Тема: аналитическая геометрия.
1) На оси
![]() найти точку
найти точку
![]() ,
для которой вектор
,
для которой вектор
![]() ортогонален вектору
ортогонален вектору
![]() ,
где
,
где
![]() ,
,
![]() .
.
Точка
![]() расположена на оси
расположена на оси
![]() ,
поэтому её координаты
,
поэтому её координаты
![]() .
Условием ортогональности векторов
является равенство нулю их скалярного
произведения, поэтому:
.
Условием ортогональности векторов
является равенство нулю их скалярного
произведения, поэтому:

Откуда получаем
![]() .
.
и
![]()
Ответ:
![]() .
.
2) Найти площадь параллелограмма,
построенного на векторах
![]() и
и
![]() ,
где
,
где
![]() ,
,
![]() и угол между векторами
и угол между векторами
![]() и
и
![]() равен
равен
![]() .
.
Площадь параллелограмма, построенного
на векторах
![]() и
и
![]() ,
можно вычислить как модуль их векторного
произведения:
,
можно вычислить как модуль их векторного
произведения:
![]()
Вычисляем векторное произведение векторов:
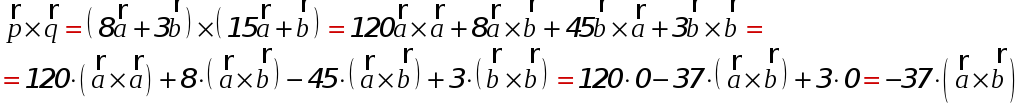
- т.к.
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, площадь параллелограмма
![]() (кв. ед.)
(кв. ед.)
Ответ:
![]() кв. ед.
кв. ед.
3) Составить уравнение прямой, проходящей
через точку
![]() ,
перпендикулярной отрезку
,
перпендикулярной отрезку
![]() ,
где
,
где
![]() ,
,
![]() .
.
Обозначим искомую прямую
![]() .
Общее уравнение прямой имеет вид
.
Общее уравнение прямой имеет вид
![]() ,
где коэффициенты
,
где коэффициенты
![]() и
и
![]() можно рассматривать как координаты
нормали прямой.
можно рассматривать как координаты
нормали прямой.
Используем в качестве нормали прямой
![]() вектор
вектор
![]() и запишем уравнение прямой как
и запишем уравнение прямой как
![]() .
.
Свободный член
![]() найдём, располагая координатами точки
найдём, располагая координатами точки
![]() :
:
![]()
и окончательно
![]() - общее уравнение прямой
- общее уравнение прямой
![]() .
.
4) Составить уравнение плоскости, содержащей прямую
![]()
и параллельной прямой
![]() .
.
Обозначим первую данную прямую
![]() ,
вторую данную прямую
,
вторую данную прямую
![]() ,
искомую плоскость
,
искомую плоскость
![]() .
Заметим, что прямые
.
Заметим, что прямые
![]() и
и
![]() неколлинеарны (не параллельны и не
совпадают). Нормальный вектор плоскости
неколлинеарны (не параллельны и не
совпадают). Нормальный вектор плоскости
![]() найдём как векторное произведение
направляющих векторов прямых
найдём как векторное произведение
направляющих векторов прямых
![]() и
и
![]() :
:
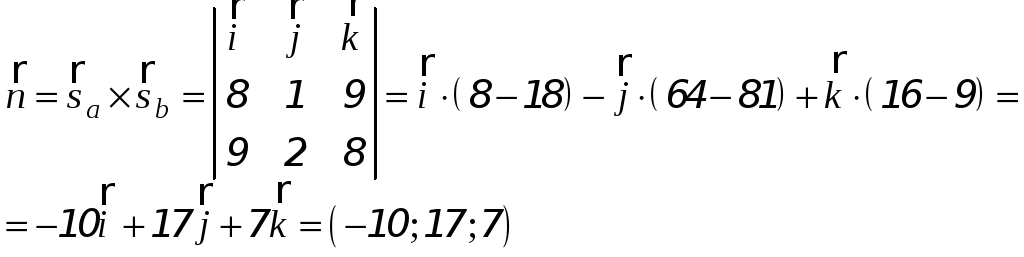
Прямая
![]() проходит, в частности, через точку
проходит, в частности, через точку
![]() .
Таким образом, уравнение плоскости
.
Таким образом, уравнение плоскости
![]() - уравнение плоскости, проходящей через
точку
- уравнение плоскости, проходящей через
точку
![]() и имеющей нормальный вектор
и имеющей нормальный вектор
![]() :
:
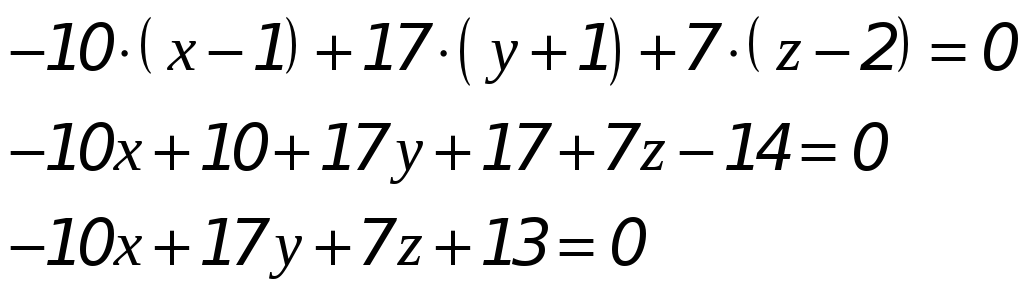
![]() - общее уравнение плоскости
- общее уравнение плоскости
![]() .
.
Тема: линейная алгебра.
5) Вычислите
![]() ,
где
,
где
 ,
,
![]() ,
,
 .
.

Вычисление в Mathcad 16:
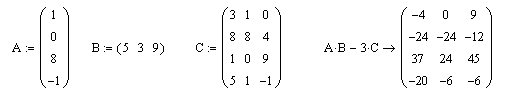
6) Решите систему линейных уравнений
![]()
а) по формуле Крамера;
б) матричным способом.
Запишем систему линейных уравнений в матричном виде
![]() ,
,
где основная матрица системы
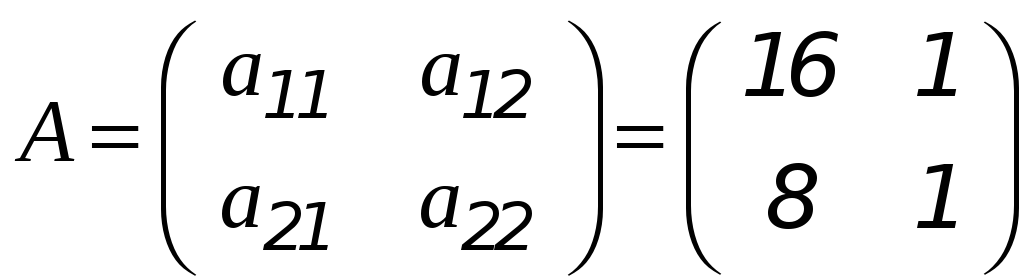
вектор неизвестных
![]()
вектор правых частей системы
![]()
а)
Решим неоднородную систему
![]() по формулам Крамера.
по формулам Крамера.
Вычисляем главный определитель:
![]() .
.
Определители
![]() ,
полученные из определителя основной
матрицы заменой
,
полученные из определителя основной
матрицы заменой
![]() -го
столбца столбиком свободных членов:
-го
столбца столбиком свободных членов:
![]()
Находим решение по формулам Крамера:
![]()
Выполним проверку найденного решения подстановкой в исходное уравнение:
 -
верно
-
верно
Ответ:
![]() .
.
б)
Матричный способ. Решение ищем в виде
![]() ,
где
,
где
обратная матрица
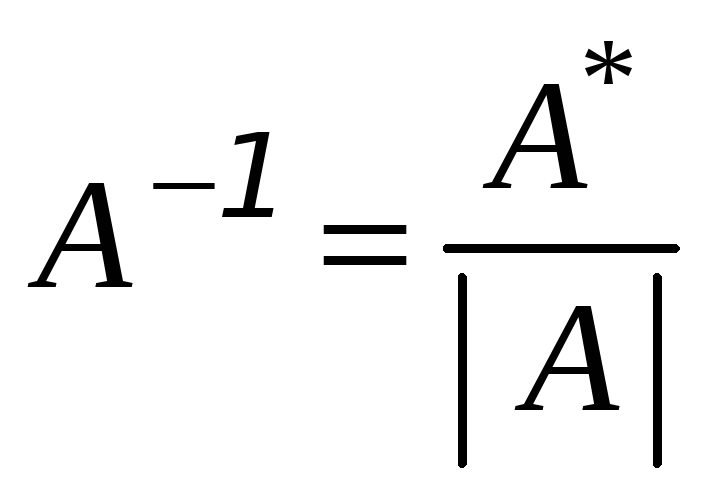 ;
;
![]() - союзная (присоединённая) матрица;
- союзная (присоединённая) матрица;
![]() -
определитель матрицы
-
определитель матрицы
![]() .
.
Вычислим определитель матрицы
![]() :
:
![]()
Союзная (присоединённая) матрица - это
транспонированная матрица алгебраических
дополнений
![]() элементов
элементов
![]() матрицы
матрицы
![]() :
:
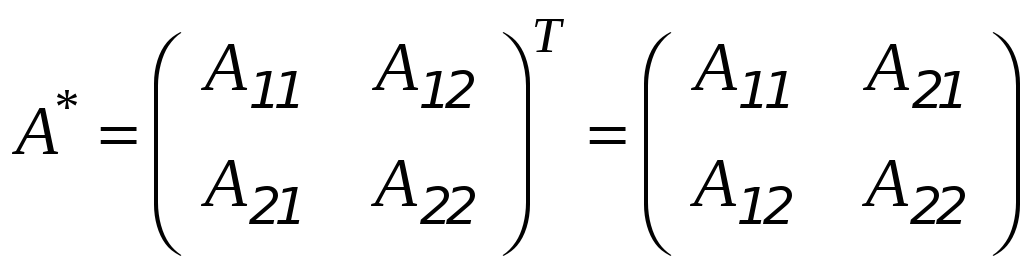
Вычисляем алгебраические дополнения
матрицы
![]() :
:
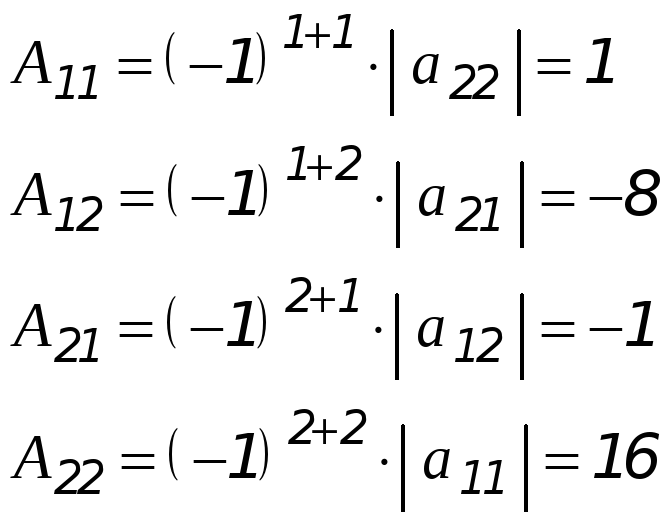
Запишем союзную (присоединённую) матрицу:
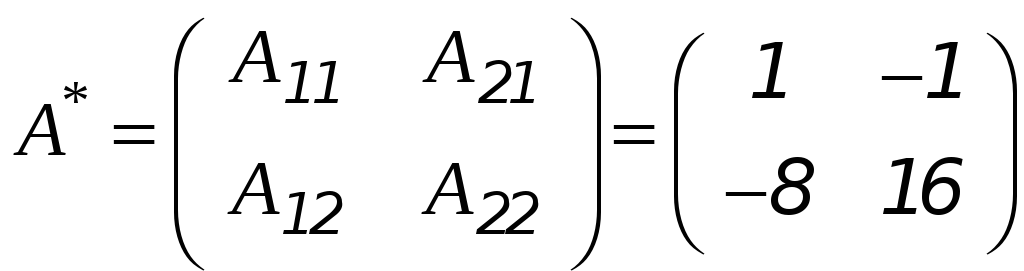
и вычислим обратную матрицу
![]()
Находим решение:
![]()
Ответ:
![]() .
.
Решение системы в Mathcad 16:
![]()
7) Найдите общее решение системы линейных уравнений
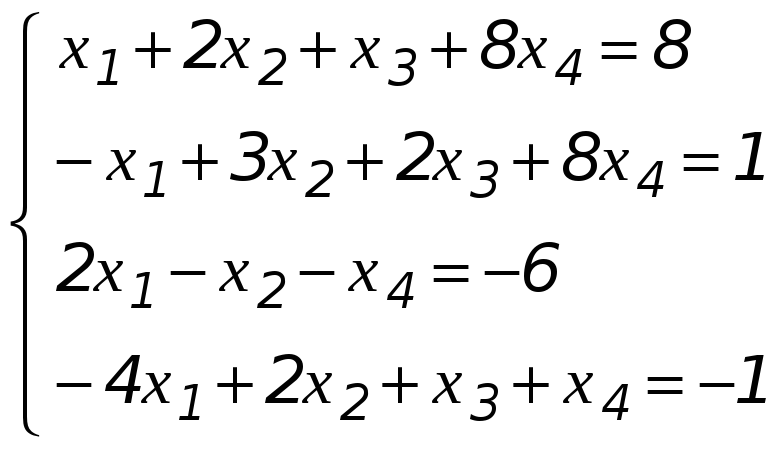
Определение. Равенства, выражающие базисные переменные через свободные, называются общим решением системы.
Теорема Кронекера-Капелли.
Система линейных
алгебраических уравнений совместна
тогда и только тогда, когда ранг
расширенной матрицы системы равен рангу
основной матрицы
![]() .
.
Теорема.
Если ранг
совместной системы равен числу неизвестных
![]() ,
то система имеет единственное решение
(система определённая).
,
то система имеет единственное решение
(система определённая).
Если ранг
совместной системы меньше числа
неизвестных
![]() ,
то система имеет бесчисленное множество
решений (система неопределённая).
,
то система имеет бесчисленное множество
решений (система неопределённая).
► Исследуем совместность системы, опираясь на теорему Кронекера-Капелли. Найдём ранги основной и расширенной матрицы системы. Чтобы не выполнять двойной работы, преобразуем сразу расширенную матрицу системы к упрощенному виду (методом Гаусса):

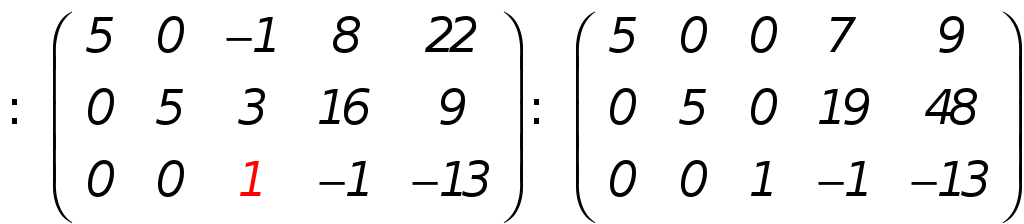
Из последней
матрицы видим, что ранги основной и
расширенной системы равны
![]() ,
следовательно, система совместна. Так
как число неизвестных
,
следовательно, система совместна. Так
как число неизвестных
![]() ,
то
,
то
![]() ,
и значит система уравнений неопределённа,
т.е. имеет бесчисленное множество
решений.
,
и значит система уравнений неопределённа,
т.е. имеет бесчисленное множество
решений.
► Решение системы.
Полученную ранее упрощенную матрицу системы запишем в виде системы:
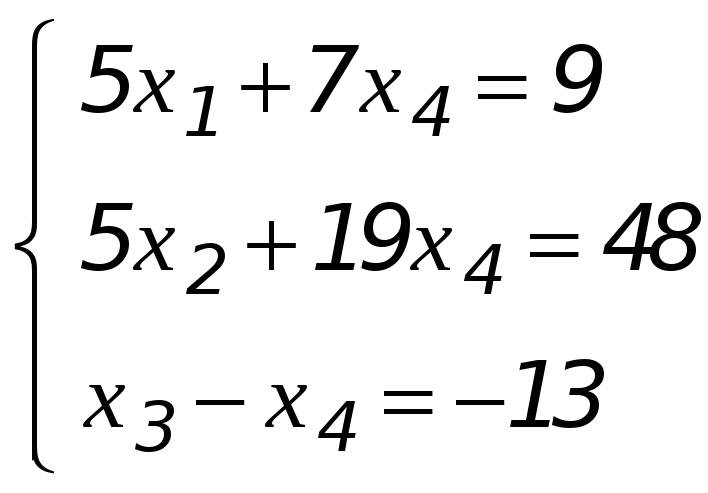
Пусть свободная переменная
![]() ;
выразив главные (базисные) переменные
;
выразив главные (базисные) переменные
![]() и
и
![]() через свободную переменную, получим
общее решение системы:
через свободную переменную, получим
общее решение системы:
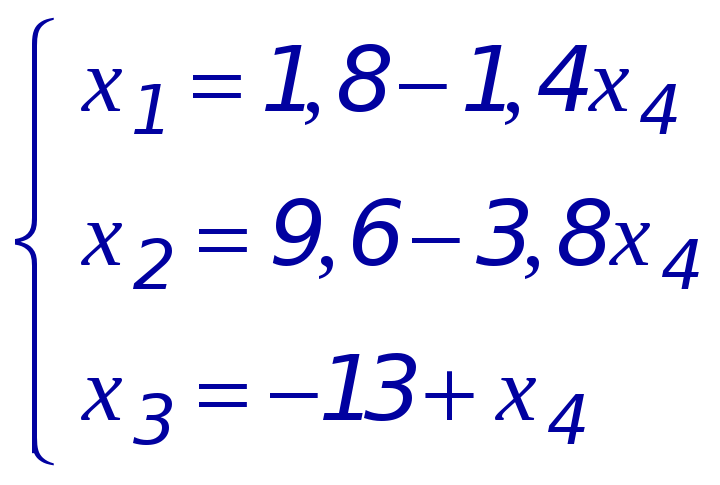
Система имеет бесконечно много решений.
Решение системы в Mathcad 16:
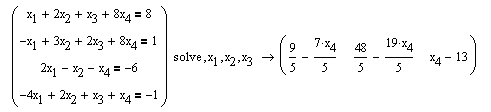
Тема: теория вероятностей.
8) В урне имеется 8 белых и 15 черных шаров. Из урны извлекают 3 шара одновременно.
а) Какова вероятность того, что среди извлечённых шаров белых шаров будет больше, чем чёрных ?
б) Найдите закон распределения случайной
величины
![]() ,
где
,
где
![]() - число белых шаров среди извлечённых.
- число белых шаров среди извлечённых.
Обозначим события:
![]() - среди вынутых из урны наугад трёх шаров
обнаружено
- среди вынутых из урны наугад трёх шаров
обнаружено
![]() белых шаров;
белых шаров;
![]() - извлечённых шаров белых шаров будет
больше, чем чёрных.
- извлечённых шаров белых шаров будет
больше, чем чёрных.
► Для начала найдём
закон распределения случайной величины
![]() .
.
Общее число возможных элементарных
исходов испытания равно числу способов,
которыми можно выбрать 3 шара из 23, т.е.
![]() - числу сочетаний из 23 элементов по 3.
- числу сочетаний из 23 элементов по 3.
Число исходов, благоприятствующих
интересующему нас событию, например,
для случая обнаружения двух белых шаров
среди трёх извлечённых из урны (среди
трёх шаров 2 белых и 1 чёрный) определим,
используя правило произведения в
комбинаторике:
![]() - из находящихся в урне 8-ми белых шаров
необходимо выбрать 2 шара, при этом из
15-ти чёрных шаров необходимо выбрать
1.
- из находящихся в урне 8-ми белых шаров
необходимо выбрать 2 шара, при этом из
15-ти чёрных шаров необходимо выбрать
1.
По формуле классического определения вероятности:
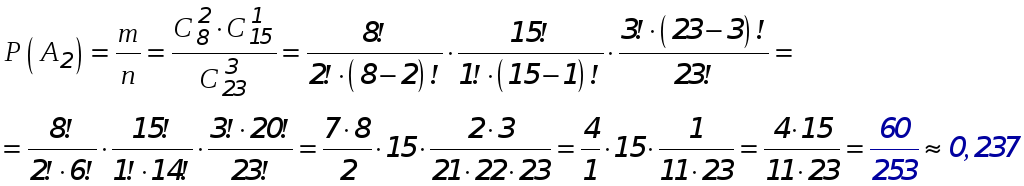
Вероятность обнаружения 0 белых шаров среди трёх вынутых из урны
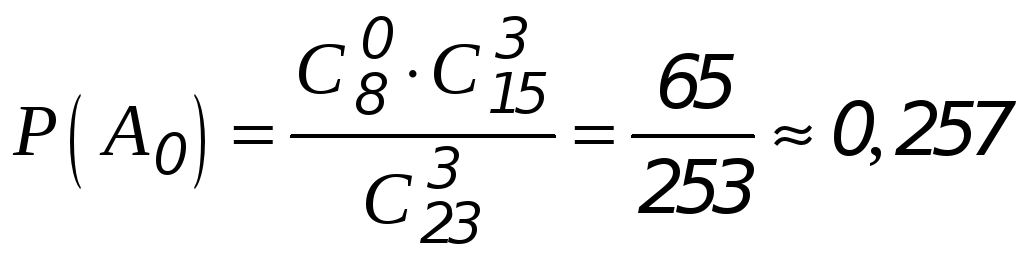
вероятность обнаружения 1-го белого шара среди трёх вынутых из урны
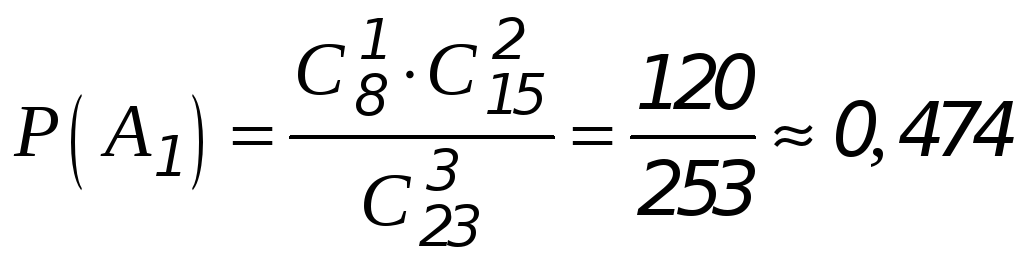
вероятность обнаружения 2-х белых шаров среди трёх вынутых из урны
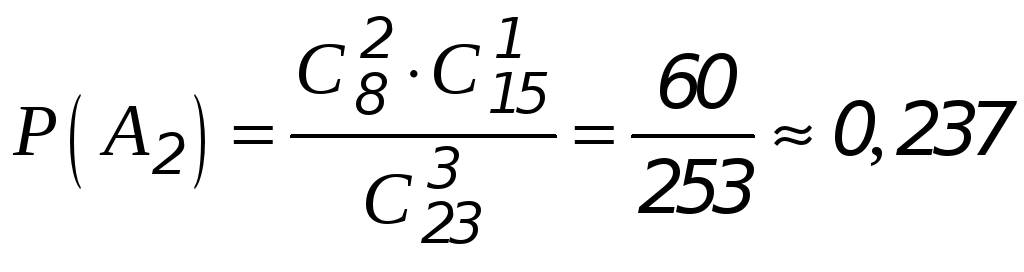
вероятность обнаружения 3-х белых шаров среди трёх вынутых из урны
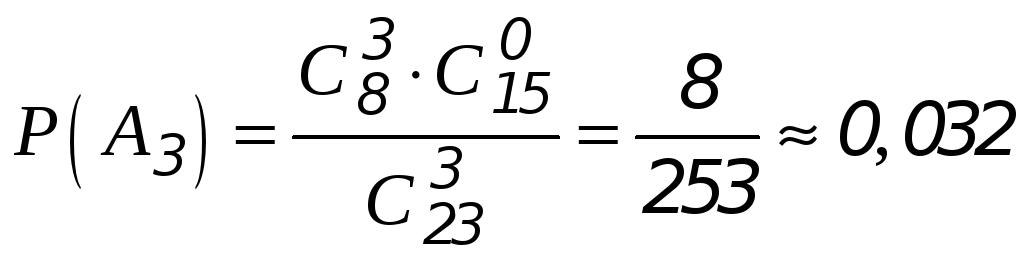
Заметим, что события
![]() составляют полную группу событий:
составляют полную группу событий:
![]()
► Запишем закон
распределения случайной величины
![]() - числа белых шаров среди трёх извлечённых
случайным образом из урны (закон
распределения дискретной случайной
величины, заданный в виде таблицы,
называется рядом распределения):
- числа белых шаров среди трёх извлечённых
случайным образом из урны (закон
распределения дискретной случайной
величины, заданный в виде таблицы,
называется рядом распределения):
-
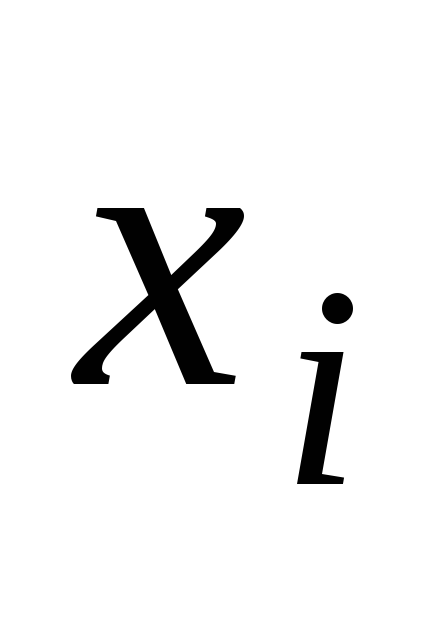
0
1
2
3
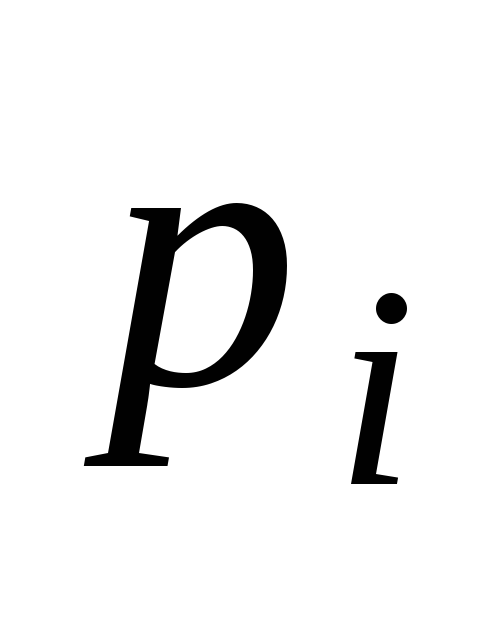
65/253
120/253
60/253
8/253
► Какова вероятность
того, что среди извлечённых шаров белых
шаров будет больше, чем чёрных ? События
![]() несовместны, поэтому к их вероятностям
применима теорема сложения вероятностей:
несовместны, поэтому к их вероятностям
применима теорема сложения вероятностей:
![]()
9) Рабочий обслуживает три станка. Каждый из станков может выходить их строя независимо друг от друга с вероятностями 0.8, 0.9, 0.5 соответственно. Стало известно, что из строя вышел один станок. Какова вероятность, что это был первый станок ?
Обозначим событие:
![]() - станок выходит из строя.
- станок выходит из строя.
Сформулируем гипотезы:
![]() - из строя вышел 1-й станок,
- из строя вышел 1-й станок,
![]() ;
;
![]() - из строя вышел 2-й станок,
- из строя вышел 2-й станок,
![]() ;
;
![]() - из строя вышел 3-й станок,
- из строя вышел 3-й станок,
![]() .
.
Условные вероятности:
![]() ;
;
![]() ;
;
![]() .
.
По формуле полной вероятности
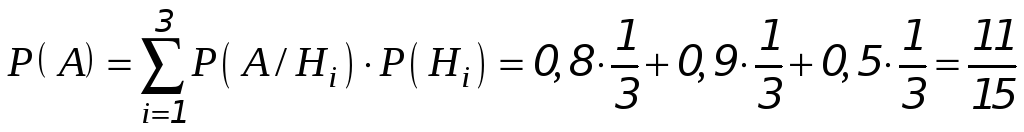
- вероятность того, что станок выйдет из строя.
Искомую вероятность найдём по формуле
Байеса (переоценка вероятности
события
![]() ):
):
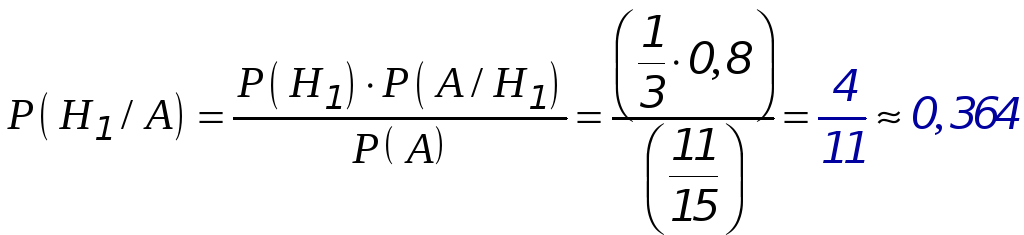
- вероятность того, что вышедший из строя станок - это первый станок.
Ответ:
![]() .
.
10) Непрерывная случайная величина
![]() задана плотностью распределения
задана плотностью распределения

Найдите:
а) функцию распределения
![]() ;
;
б) математическое ожидание
![]() ;
;
в) вероятность того, что в результате
испытания
![]() примет значение из интервала
примет значение из интервала
![]() ;
;
г) вероятность того, что в трёх испытаниях
![]() ровно два раза принимает значение,
принадлежащее интервалу
ровно два раза принимает значение,
принадлежащее интервалу
![]() .
.
![]() - плотность распределения (плотность
распределения вероятностей, плотность,
дифференциальная функция распределения)
случайной величины
- плотность распределения (плотность
распределения вероятностей, плотность,
дифференциальная функция распределения)
случайной величины
![]() ;
;
![]() .
.
![]() - функция распределения (функция
распределения вероятностей, интегральная
функция распределения) случайной
величины
- функция распределения (функция
распределения вероятностей, интегральная
функция распределения) случайной
величины
![]() ;
;
 .
.
► Для вычисления
интегральной функции распределения
используем формулу
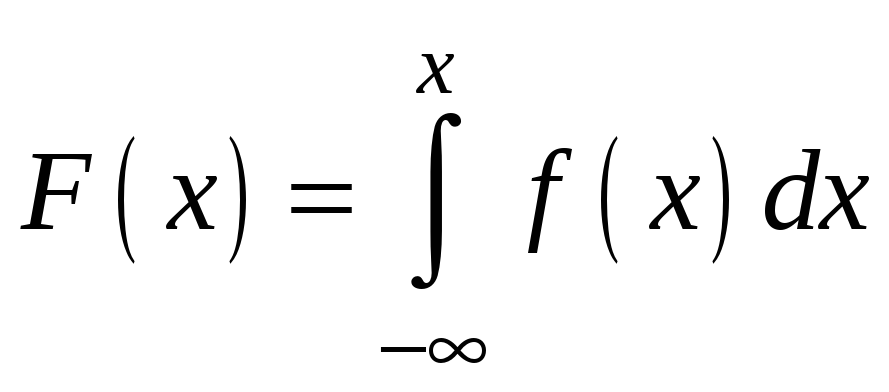 .
.
Если
![]() ,
то
,
то
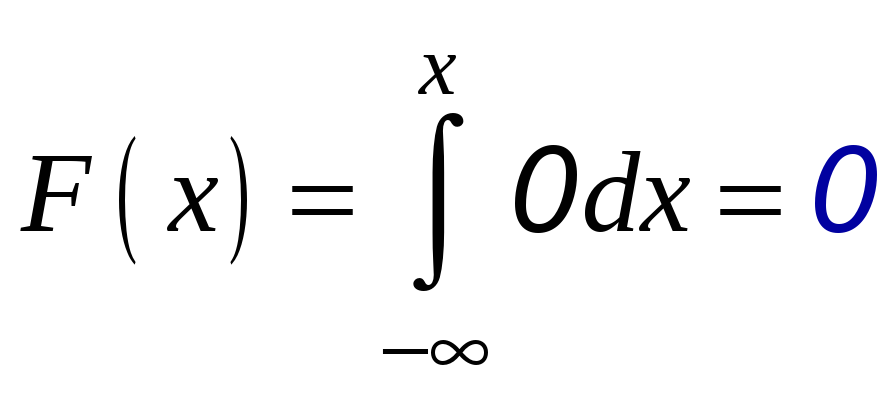 .
.
Если
![]() ,
то
,
то
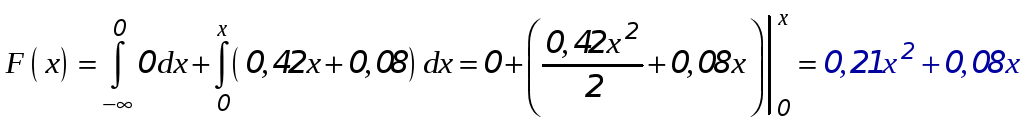 .
.
Если
![]() ,
то
,
то
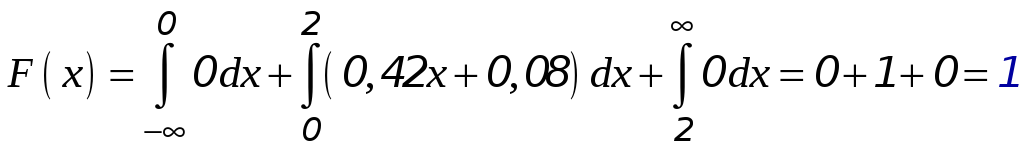 .
.
Итак, интегральная функция распределения:
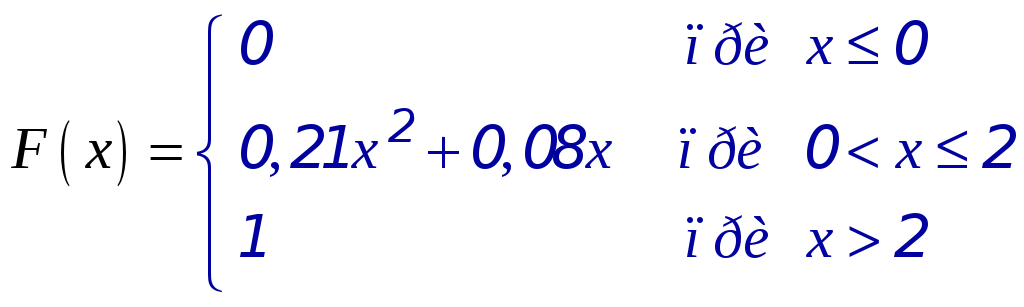
► Математическое ожидание
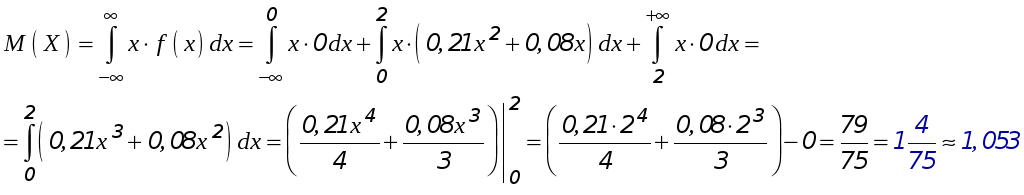
► Вероятность того,
что случайная величина примет значение
из интервала
![]() :
:
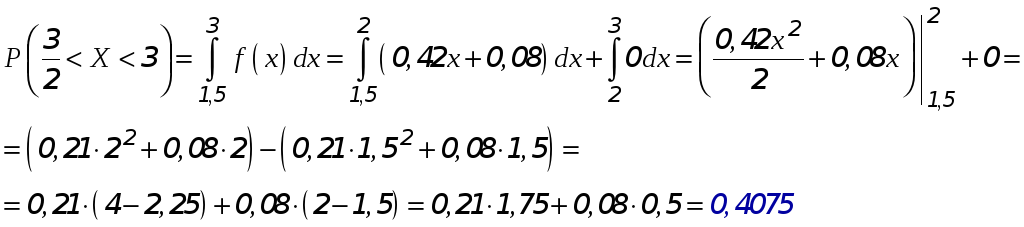
или, через функцию распределения:
![]()
► Вероятность того,
что в трёх испытаниях
![]() ровно два раза принимает значение,
принадлежащее интервалу
ровно два раза принимает значение,
принадлежащее интервалу
![]() .
.
Обозначим событие:
![]() - в трёх испытаниях
- в трёх испытаниях
![]() ровно два раза принимает значение,
принадлежащее интервалу
ровно два раза принимает значение,
принадлежащее интервалу
![]() .
.
Вероятность того, что случайная
величина в одном испытании примет
значение из интервала
![]() :
:
![]()
Условия задачи соответствуют схеме Бернулли, и вычисления производим по формуле Бернулли
![]()
Искомая вероятность
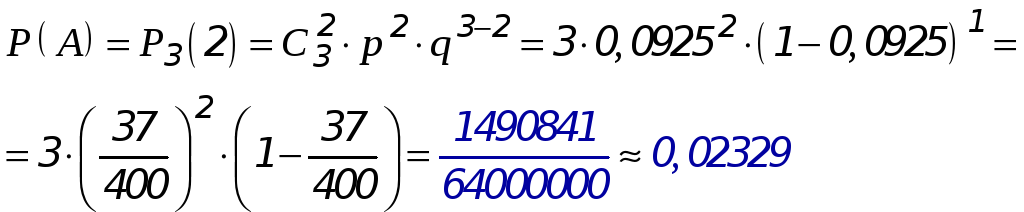
Ответ:
![]() .
.
