10. Уравнения вида и

Решение уравнений, не содержащих в одном случае аргумента , а в другом – функции, ищем в параметрической форме, принимая за параметр производную неизвестной функции

Для уравнения первого типа получаем:

Делая замену, получаем:

В результате этих преобразований имеем дифференциальное уравнение с разделяющимися переменными:

Общий интеграл в параметрической форме представляется системой уравнений

.

Исключив из этой системы параметр , получим общий интеграл и не в параметрической форме.

Для дифференциального уравнения вида с помощью той же самой подстановки и аналогичных рассуждений получаем результат:

.

11. Уравнения Лагранжа и Клеро

Уравнением Лагранжа называется дифференциальное уравнение, линейное относительно и, коэффициенты которого являются функциями от:

.

Для нахождения общего решение применяется подстановка :

Дифференцируя это уравнение c учетом того, что , получаем

Если решение этого (линейного относительно ) уравнения естьто общее решение уравнения Лагранжа может быть записано в виде

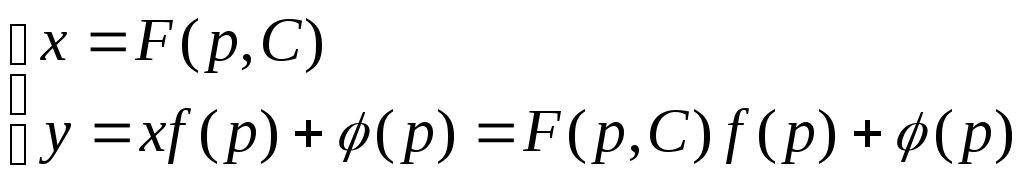
Уравнением Клеро называется уравнение первой степени (то есть линейное) относительно функции и аргумента вида

Вообще говоря, уравнение Клеро является частным случаем уравнения Лагранжа. С учетом замены уравнение принимает вид

.

Это уравнение имеет два возможных решения:

или

В первом случае

.

Видно, что общий интеграл уравнения Клеро представляет собой семейство прямых линий. Во втором случае решение в параметрической форме выражается системой уравнений

.

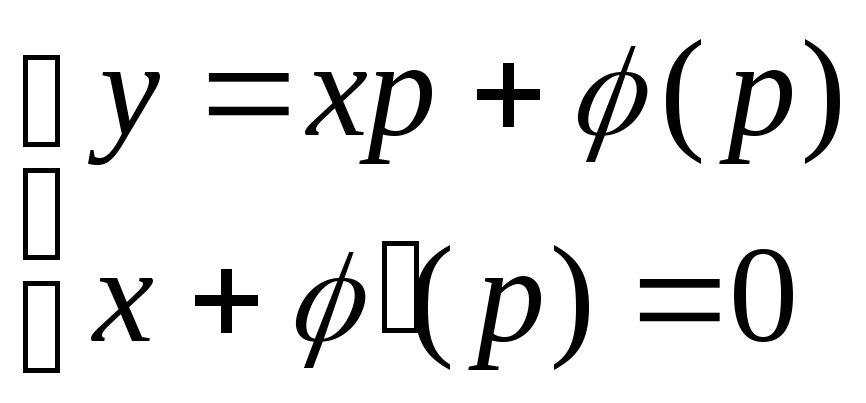Исключая параметр , получаем второе решение . Это решение не содержит произвольной постоянной и не получено из общего решения, следовательно, не является частным решением. Это решение будет являться особым интегралом.

12. Определение типа дифференциального уравнения первого порядка

Для выбора пути решения заданного дифференциального уравнения первого порядка сначала надо определить тип, к которому оно относится. Для этого следует разрешить данное уравнение относительно производной, то есть привести его к виду . После этого надо посмотреть, не разлагается ли функцияна множители, один из которых зависит только от, а второй – только от. Если это возможно, то надо разделить переменные и интегрировать обе части получившегося равенства.

Если переменные не разделяются непосредственно, то следует проверить, является ли данное уравнение линейным или уравнением Бернулли, то есть имеет ли функция видили.

К уравнению Бернулли также сводятся уравнения вида (и более общего вида). Для их решения надо поменять местами переменныеии считатьфункцией от. В результате для этой функции получим линейное уравнение:(или уравнение Бернулли). Например, уравнение, еслисчитать аргументом, а– функцией, принимает вид, то есть становится линейным.

Если и этот метод не приводит к цели, следует проверить, не является ли однородной функцией нулевой степени. Наконец, если и этот метод окажется неудачным, надо записать заданное уравнение в видеи проверить, не является ли оно уравнением в полных дифференциалах.

§2. Уравнения высших порядков

1. Дифференциальное уравнение называетсяуравнением п-го порядка. Его общее решение содержит п произвольных постоянных: , а решение задачи Коши требует задания прих = х₀ значений функции у и ее производных до (п – 1)-го порядка включительно:

2. Если в дифференциальное уравнение не входит явным образом искомая функция у, то есть уравнение имеет вид

,

то можно понизить его порядок на k единиц, сделав замену: Тогда

Типовой пример

Найти общее решение уравнения

►Пусть ТогдаТеперь трижды проинтегрируем полученное равенство пох:

◄

3. Если дифференциальное уравнение не содержит явно независимую переменную х: то можно понизить его порядок на единицу, считая, чтоТогда, то есть вторая производнаяу выражается через первую производную р и т.д.

Типовой пример

Решить задачу Коши для уравнения , еслиу(1)=2, у’(1)=2.

►Замена приводит к уравнениюоткуда:

а) р = 0, у’ = 0, у = С, но у’ (1)=2 ≠ 0, значит, в этом случае решения нет;

б)

Тогда

Следовательно, искомое частное решение имеет вид

◄