Задания для самостоятельного решения

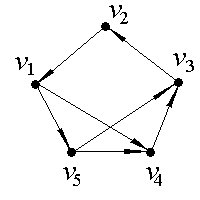
1. С помощью матрицы смежности найти компоненты сильной связности ориентированного графа D.

а)	б)	в)

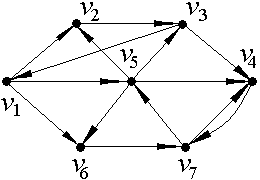
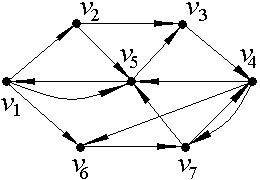
2. С помощью алгоритма фронта волны найти расстояния в ориентированном графе D: диаметр, радиус и центры.

а)	б)	в)

Примечание: самый длинный путь в графе найти при помощи алгоритма фронта волны.

Практическое занятие 3

«НЕЧЕТКИЕ МНОЖЕСТВА И НЕЧЕТКАЯ ЛОГИКА»

Рассмотрим различные подмножества А универсального множества I (при I=R это будут множества вещественных чисел - фрагменты числовой оси, при I = R² - области плоскости). Каждому А поставим в соответствие характеристическую функцию принадлежности m_A(х) - предикат, определяющий А следующим образом:

Пример. Для отрезка числовой прямой А = [1, 2] имеем ступенчатую функцию

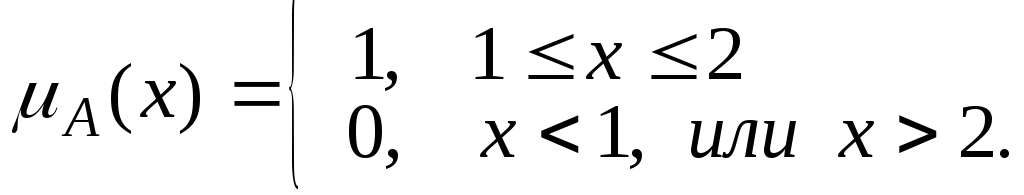
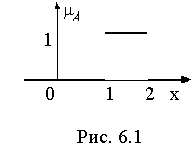
Очевидно "х m_I(х) º 1; m_Æ(х) º 0. Характеристические функции обладают следующими свойствами:

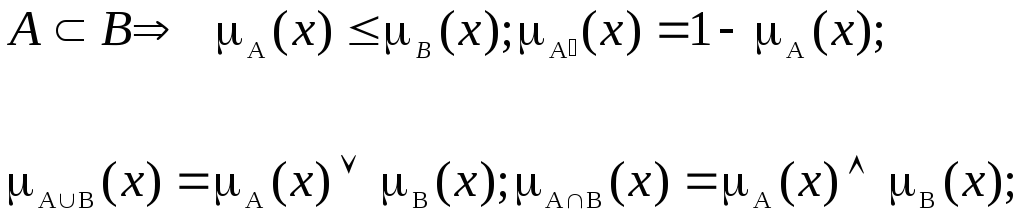(1)

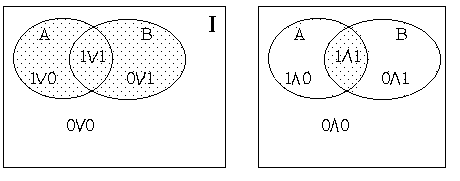
которые проверяются непосредственным анализом всевозможных случаев (рис. 6.2).

Рис. 6.2

Предикат m_A(х) можно рассматривать, как связующее звено между двумя представителями булевых алгебр - алгеброй множеств и алгеброй логики.

Две нижние формулы (1) остаются справедливыми, если в качестве операций Ú, Ù над m_A и m_В применять не дизъюнкцию и конъюнкцию, а взятие максимума и минимума:

pÚq = max{p,q}, pÙq = min{p,q}: (2)

или же задать их посредством алгебраических операций сложения и умнoжeния

pÚq = p + q - p×q, pÙq = p×q. (3)

(например, проверка формулы m_АÈВ = m_А + m_В - m_А m_В для случая х Î АÇВ дает:

1 = 1 + 1 - 1×1,

проверяя формулу m_АÇВ = min{ m_А, m_В} при х Î А\В, получим : 0 = min{1, 0}.)

Приведем пример, когда категоричная однозначность (да, или нет) характеристической функции приводит к неэффективным результатам.

Рассмотрим алгоритм, управляющий движущимся транспортом. Формализуем правило «если скорость велика, то тормозить» следующим образом. Пусть v_maх - предельно допустимая скорость движения. Множество V опасных скоростей определим характеристической функцией:

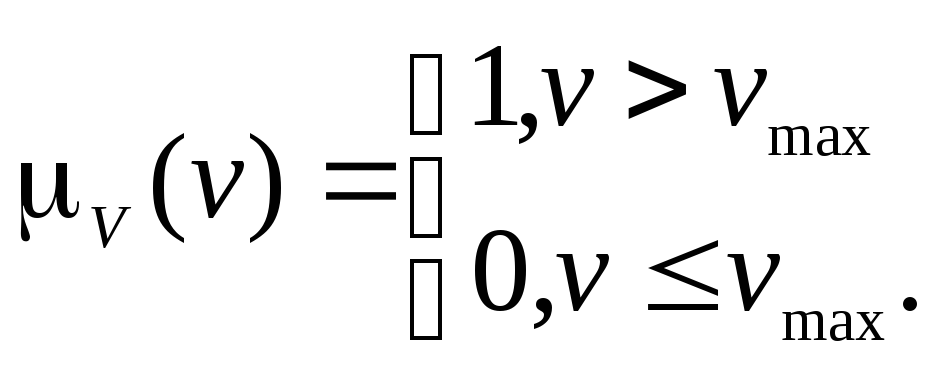
Тогда управляющую команду на включение тормоза в момент времени T можно задать булевой переменной u(T) = m_V[v(T)], где v(T) - результат текущего измерения скорости. Приведенный алгоритм моделирует поведение неопытного водителя, нервирующего пассажиров частыми рывками. Навыки квалифицированного водителя словесно описываются более гибким правилом: «если скорость велика, то тормозить; если близка к предельной, то притормозить», в которое входят нечеткие понятия «близка к предельной» и «притормозить». Математическая формализация перечисленных выражений приводит к нечеткому множеству V опасных скоростей с размытой границей и к многозначной логической переменной u, принимающей ряд промежуточных значений между нулем-бездействием и единицей - экстренным торможением.

Восприятие и обработка нечетких образов (облако в небе, клякса на промокашке - геометрические примеры нечетких множеств в R³ и в R²), гибкость и неоднозначность логических суждений (да, скорее всего, вероятно, вряд ли, нет), характерные для человеческого мышления, являются предметной областью систем искусственного интеллекта, использующих аппарат нечеткой математики, начало которой было положено статьей «Нечеткие множества » американского ученого Л. Заде, опубликованной в 1965 г. Основываясь на гипотезе о том, что «человек мыслит не числами, а нечеткими понятиями», Заде расширил двузначную оценку принадлежности элемента х множеству А: m_А(x)Î {0,1} до многозначной оценки выше 0 и ниже 1: m_А(x) Î [0,1] (напомним, что {0,1} - множество из двух чисел, а [0,1] - отрезок числовой оси, содержащий бесконечное множество точек). Задание нечеткого множества функцией принадлежности

m_А(x) Î [0,1] можно интерпретировать следующим образом: «величина m_А(x) отражает субъективную оценку степени принадлежности х множеству А, например, m_А(x) = 0.8 означает, что х на 80% принадлежит А». В случае графического представления диаграмма Эйлера-Венна заменяется концентрическими областями (рис. 6.3,а), а при А Ì R ступенчатый график m_А(x) (рис. 1) преобразуется в колоколообразный (рис. 6.3,b):

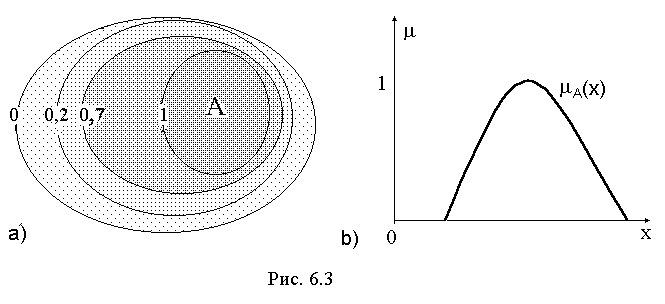
Точное определение нечеткого множества можно сформулировать так. Пусть I - универсальное множество и х Î I. Нечетким подмножеством множества I называется множество упорядоченных пар

{ x | m_А(x)} "x ÎI,

где m_А(x) - функция принадлежности, принимающая свои значения в множестве принадлежности М. Обычно М = [0, 1]. Понятие нечеткого множества является расширенным понятием, охватывающим и понятие четкого множества, как частный случай при М = {0, 1} Ì [0, 1].

Нечеткое множество можно рассматривать, как систему вложенных подмножеств различного уровня (рис. 6.3,a). Пусть a Î [0,1]. Подмножеством a-уровня нечеткого множества А называется обычное (четкое) подмножество

А_a = {x | m_А(x) ³ a}.

Четким подмножеством , ближайшим к нечеткому множеству А называется множество с характеристической функцией

(отметим, что, вообще говоря, !). Перейдем к примерам.

Рассмотрим в качестве универсального множества латинский алфавит

I = {a, b, c, ..., z}. Обозначая n-ю по счету букву через х_n и полагая

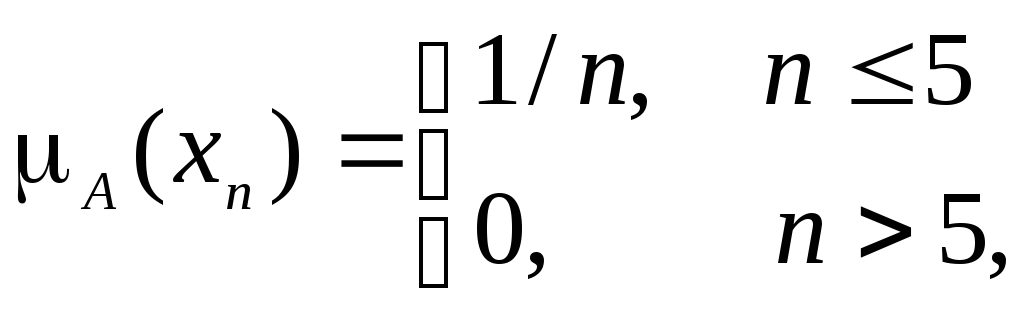
(например, m_А(b) = 1/2; m_А(n) = m_А(x₁₄) = 0), определим нечеткое понятие «начало алфавита», как множество

или более наглядно (пары с нулевым значением m_А можно опустить):

Подмножествами уровней a = 0,3 и a = 0,6 будут: A_0,3 = {a,b,c}, A_0,6 = {a}. Четким подмножеством, ближайшим к началу алфавита будет ={a}, тогда как A_0,5 = {a,b}.

Мерой близости между нечеткими множествами A и B, содержащими n элементов, является расстояние Хэмминга, которое определяется с помощью формулы

.

Например, для расстояние Хэмминга равноd_H (A,B) = |0,7-0,2| + |0,2-0| + |0-1| + |0,6-0,6| = 1,7.

Итак, нечеткое множество полностью определяется функцией принадлежности m_А(x), которую по аналогии с четкими случаями можно называть многозначной логической переменной, или нечетким предикатом. При этом основные свойства и операции для нечетких множеств (см. формулы (1)) будут определяться соответствующими операциями над их функциями принадлежности. Так, включение нечеткого множестваАв нечеткое множествоВ(т. е.,А Ì В) эквивалентно неравенствуm_А(x)£m_В(x), дополнениеА¢нечеткого множества определяется функцией(см. рис. 6.4):

Рис. 6.4

Однако, результаты операций пересечения и объединения теперь будут зависеть от того, как мы определим операции Ù и Ú для функций принадлежности. На рис. 6.5,a приведены функции принадлежности для АÇВ и АÈВ, определенные по формулам (2):

m_АÇB(x) = m_А(x)Ù m_B(x) = min{m_А(x), m_B(x)},

m_АÈB(x) = m_А(x)Ú m_B(x) = max{m_А(x), m_B(x)}.

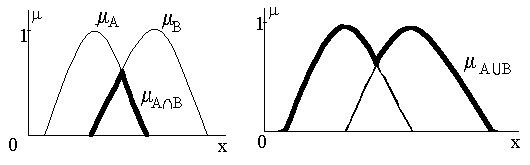
a) m_АÇB(x) = min{m_А(x), m_B(x)} m_АÈB(x) = max{m_А(x), m_B(x)}

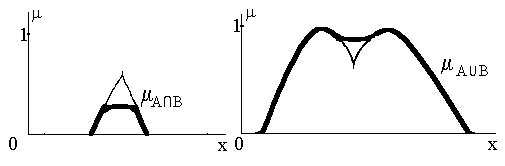
b) m_АÙ m_B = m_А×m_B m_АÚ m_B = m_А + m_B -m_А×m_B

Рис. 6.5

На рис. 6.5,b приведены результаты применения формул (3) для определения операций пересечения и объединения нечетких множеств:

m_А(x)Ù m_B(x) = m_А(x) ×m_B(x), m_А(x)Ú m_B(x) = m_А(x) + m_B(x) - m_А(x)×m_B(x).

Выясняя, какая часть аппарата традиционной логики сгодится для решения нечетких задач, отметим невыполнение некоторых законов булевой алгебры для нечетких множеств. Например, нарушен закон , так как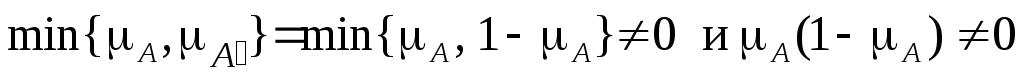; нарушен закон, так как

(см. рис. 6.6):

Рис. 6.6

Рассмотрим единичный куб, вершины основания которого являются областью определения булевых функций (рис. 6.7).

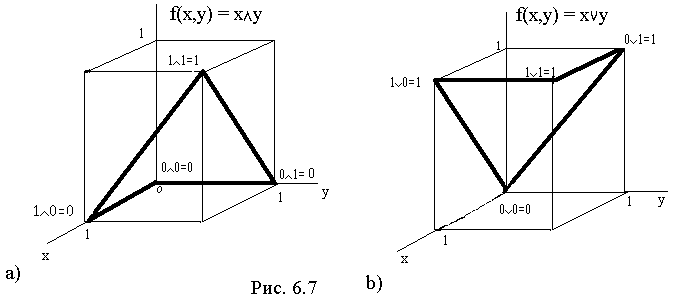
При корректном расширении двоичных бинарных операций (булевых функций табл. 2, стр. 10) на область нечетких значений - внутренность единичного куба - естественно потребовать, чтобы их поведение на границе совпадало с результатами соответствующих аналогов. Соединив прямыми линиями четыре вершины куба, соответствующие табличным значениям булевых функций, получим каркас граничных условий, однозначно характеризующий каждую из 16-ти операций.

На рис. 6.7,а изображен каркас конъюнкции f(x,y) = xÙy, на рис. 6.7,b - дизъюнкции f(x,y) = xÚy. «Физическим» решением задачи их расширения на внутренность единичного квадрата х,у Î[0,1], будет погружение соответствующих каркасов в мыльный раствор. Пленки, натянутые на каркасах после их вынимания из раствора, будут являться минимальными поверхностями, обладающими наименьшей площадью, а функции двух вещественных переменных, графики которых совпадут с полученными поверхностями, можно трактовать как искомые расширения.

Гладкие функции f(x,y) = xy и f(x,y) = x + y - xy, соответствующие формулам (3), являются хорошим приближением к минимальным поверхностям (рис. 6.8,a).

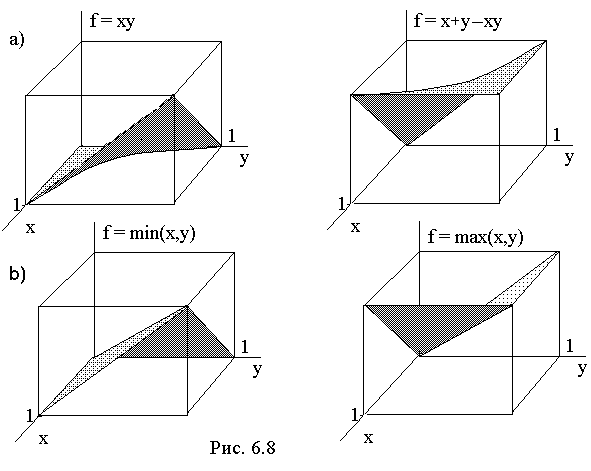
Кусочно-гладкие функции f = min{x,y} и f = mах{x,y} приближают минимальные поверхности набором плоскостей с изломом по диагонали куба (рис. 6.8,b).

Для всех 16 булевых функций - бинарных операций гладкие расширения в область нечетких переменных могут быть получены из вероятностных соображений.

Будем рассматривать значения нечеткой логической переменной, как вероятность Р(А) случайного события А, а результат логической операции, как вероятность составного случайного события. Вычислим вероятность нечеткой конъюнкции Р(АÙВ), для которой справедлива следующая таблица истинности:

A B AÙB	0 0 0	0 1 0	1 0 0		1 1 1
число исходов	N0×M0	N0×M1	N1×M0	N1×M1

Здесь N0,N1 - число неблагоприятных и благоприятных исходов для А; M0, M1 - число неблагоприятных и благоприятных исходов для B. Обозначим общее число испытаний А и В через N = N0+N1 и M = M0+M1, соответственно. Из таблицы видно, что вероятность благоприятных исходов для операции равна

,

где P(A) = N1/N, P(B) = M1/M. Вероятность остальных операций вычисляется аналогично. Например,

(в терминах функции принадлежности:

По сравнению с нечеткими операциями, использующими максиминную основу (см. формулы (2)), вероятностные операции не могут обеспечить точное выполнение некоторых законов булевой алгебры. Так, для нечетких переменных

а = m_A(х) и b = m_B(х) не выполняются законы идемпотентности:

не выполняется закон дистрибутивности: , так как

Об этом следует помнить при упрощении нечетких функций f(a,b) нечетких переменных. Однако эти нарушения несущественны: законы выполняются приближенно с достаточной для нечетких задач точностью. Более того, сглаживающий характер вероятностных операций обеспечивает меньшее, чем у

максиминных, отклонение от законов комплементарности (см. рис. 6.6). Оптимальный выбор нечетких операций в каждом конкретном случае зависит от характера поставленной задачи.

Пример. Дано нечеткое множество Найтииспользуя а) вероятностные; б) максиминные операции над множествами.

Решение.

a) Найдем М¢, используя

Найдем М¢М, используя

Найдем М¢МÈМ, используя

б) Так как для максиминных операций выполняются все законы булевой

алгебры, кроме комплементарных, упростим функцию принадлежности для

М¢МÈМ, введя обозначения m = m_M(x), ^Øm = m_M¢(x).

Используя дистрибутивный закон, получим:

m^ØmÚm = m(^ØmÚ1) = m×1 = m, то есть:

Отличие от результата а) заключается в отклонении на 0.056.

Рассмотрим практические задачи, приводящие к нечетким множествам.

Автоматизация управления пассажирским транспортом. Формализуем с помощью нечетких множеств правило плавного управления скоростью: «Если скорость большая, то тормозить, если довольно высока, то притормозить».

Уяснив у эксперта-водителя смысл предпосылок «скорость большая» - «примерно 20 м/с» , «довольно большая» - «примерно 17 м/c», опишем их нечеткими множествами:

; .

Нечеткое управление «тормозить» - «повернуть рукоятку тормоза градусов на 90» можно задать множеством (см. непрерывные расширенияV, V₁, U на рис. 6. 9).

Задача ставится следующим образом. На основе известных нечетких множеств V,U и результата текущего измерения, оформленного в виде V₁, определить управляющее воздействие - команду исполнительному механизму.

На рис. 6.10 графически изображен процесс решения проблемы.

Cлева как VÇV₁ получен результат приближенного сопоставления предпосылки правила V и данных измерения V₁. Затем определяется максимальное значение , как некая мера сопоставленияVÇV₁. Управляющее воздействие, равное значению левой границы U_a (подмножества a-уровня множества U), будет обеспечивать плавность изменения скорости. В самом деле, дрейф текущего значения скорости V₁ влево приводит к уменьшению a и, следовательно, к сокращению величины тормозного усилия. С другой стороны, a®1 при увеличении текущей скорости, что будет вызывать экстренное торможение. В заданных конкретных условиях, полагая получим

; a = 0,6; U_0,6 = {60, 75, 90}

и управляющее воздействие составит 60°.

Работа службы знакомств. Рассмотрим вопрос о работе службы знакомств. Желающими найти друг друга могут быть как одинокие мужчины и женщины, прибегающие к услугам брачной конторы, так и безработные c работодателями, обращающиеся в биржу труда. В обоих случаях два непересекающихся множества клиентов ищут подходящих партнеров, сообщая о себе точную информацию (во избежание будущих разочарований). C другой стороны, требования к кандидатам целесообразно предъявлять в нечетком виде для расширения круга потенциальных партнеров (категорическая форма запросов, типа «не ниже 170 см», может оставить за бортом перспективного во многих отношениях жениха, не добравшего до планки пары сантиметров). Для простоты будем использовать только две характеристики клиентов службы знакомств - возраст и доход. Поскольку бедных и старых обычно просят не беспокоиться, ограничимся двумя градациями каждого из факторов, представленными в виде четырех нечетких множеств (рис. 6.11).

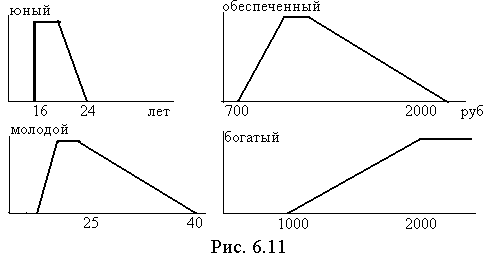
В базе данных брачной конторы хранятся следующие сведения о клиентах:

возраст	Доход	имя	кого желает
20 38 45	500 800 2000	Андрей Борис Вадим	юную, обеспеченную богатую молодую

возраст	Доход	имя	кого желает
18 38 30 23	300 1900 800 400	Галя Даша Елена Жанна	юного, обеспеченного обеспеченного богатого молодого, богатого

Требуется предоставить каждому клиенту интегральную оценку всех кандидатур по степени их перспективности.

Сократим имена клиентов до первой буквы и образуем нечеткие множества-характеристики клиентов сопоставлением их данных с эталонными профилями на рис. 6.11:

юные невесты: , юные женихи:

молодые невесты: , молодые женихи:

богатые невесты: , богатые женихи:

обеспеченные невесты: ,

обеспеченные женихи:

Информация для клиентов Б, В, Д, Е, предъявляющих к партнерам только одно требование, уже сформирована. Остается корректно сочетать в едином критерии степени обладания различными свойствами. Возможные случаи объединения количественных оценок свойств х и у (в порядке возрастания благожелательности) иллюстрирует цепочка неравенств:

xy < min{x,y} < max(x,y) < x + y - xy < x + y "x,y Î (0,1).

Крайние варианты можно предложить самым придирчивым (ху), или же неразборчивым (х+у) клиентам. Центральный вариант max{x,y}, соответствующий одной из операций объединения нечетких множеств, в данных задачах может ущемить «всесторонне развитую» личность, отдав предпочтение претенденту с «однобоким » развитием (например, max{0.8, 0.8} < max{0.9, 0}. Поэтому (хоть на приводимом примере это не сказывается) для рассматриваемых задач целесообразно использовать функцию принадлежности вероятностной операции объединения множеств: х + у - ху. Оцениваем клиентов по двум критериям

для Андрея: ;

для Гали:

для Жанны:

Полученный материал компактно оформляется в виде левой таблицы, информирующей по строкам женихов, и правой таблицы, информирующей по столбцам невест:

	Г Д Е Ж		Г	Д	Е	Ж
A	1 0,2 0,2 0,2	А Б В	0,7 0,2 0,2	0 0,2 0,2	0 0 1	1 0,2 1
Б	0 0,9 0 0
В	0,3 0,2 0,6 1

Простейшее, что можно на данном этапе предложить клиентам - это четкие подмножества, ближайшие (m > 0,5) к полученным нечетким объединениям. Однако, в этом случае Даше достанется пустое множество, а Жанне придется выбирать между взаимоисключающими крайностями {A,B}. Такие результаты свидетельствуют о целесообразности дальнейшей обработки имеющейся информации с целью улучшения отбора клиентов.