
дгту / колосов / математика / Математика к.р.1
.docx
Контрольная работа №1
Вариант 3
Задание 1. Дана
матрица
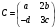 .
Найти матрицу R = C2
– 2CT
-3C-1.
.
Найти матрицу R = C2
– 2CT
-3C-1.
а = 1, b = -3, c = 1, d = -4.
 ,
,
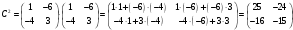 ,
,
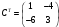 ,
,
Найдем обратную матрицу С-1.
Главный определитель:
∆ = (1•3-(-6)•(-4)) = -21
Алгебраические дополнения транспорированной матрицы:
С11=(-1)1+1·3=3; С12=(-1)1+2·(-6) = 6; С21=(-1)2+1·(-4)=4; С22=(-1)2+2·1=1;
Тогда обратная матрица имеет вид:
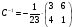
Проверим правильность нахождения обратной матрицы, умножив исходную матрицу на обратную. Должны получить единичную матрицу E.

Найдем матрицу R:
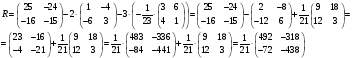
Задание 2. Дана система уравнений АХ = В, где матрицы

а = 1, b = -3, c = 1, d = -4.

Решить систему уравнений тремя методами:
а) по формулам Крамера,
б) матричным методом,
в) Методом Жордана-Гаусса.
а) Решение СЛАУ методом Крамера:
Найдем главный определитель матрицы:
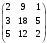 Δ
= 2(18.2-12.5)
-
9(3.2
– 5
.5)
+ (3.12
– 5
.18)
= -48
+ 171
-
54
= 69.
Δ
= 2(18.2-12.5)
-
9(3.2
– 5
.5)
+ (3.12
– 5
.18)
= -48
+ 171
-
54
= 69.
Заменим 1-ый столбец матрицы А на вектор результата В:

Δх1 = -9(2.(-6) – 5 .(-9)) + (12.(-6) – 18 .(-9)) = -297 + 90 = -207.
Заменим 2-ый столбец матрицы А на вектор результата В

Δх2 = 2.(2.(-6) – 5 .(-9)) + (3.(-9) – 5 .(-6)) = 66 + 3 = 69.
Заменим 3-ый столбец матрицы А на вектор результата В

Δх3 = 2.(18.(-9)-(-6).12) - 9(3.(-9) –5 .(-6)) = -180 - 27 = -207.
Неизвестные переменные xi:

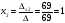
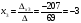
Проверка: 2.(-3) + 9.1 + 1.(-3) = 0.
3. (-3) + 18.1 + 5. (-3) = -6.
5•(-3) + 12•1 + 2•(-3) = -9.
б) Решение матричным методом:
Найдем главный определитель матрицы:
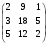 Δ
= 69 – система будет иметь решение, так
как определитель не равен нулю.
Δ
= 69 – система будет иметь решение, так
как определитель не равен нулю.
Найдем обратную матрицу через алгебраические дополнения транспорированной матрицы:
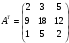
Алгебраические дополнения.
A11 = (-1)1+1(18.2 – 5.12) = -24,
A12 = (-1)1+2(2.9 – 12) = -6,
A13 = (-1)1+3(45 – 18) = 27,
A21 = (-1)2+1(6 – 25) = 19,
A22 = (-1)2+2(2.2 – 5) = -1,
A23 = (-1)2+3(10– 3) = -7,
A31 = (-1)3+1(18*5 – 3*12) = 54,
A32 = (-1)3+2(24– 45) = 21,
A33 = (-1)3+3(36 – 27) = 9,
Обратная матрица:
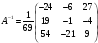
Вектор результатов:
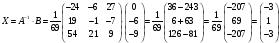
Проверка: 2.(-3) + 9.1 + 1.(-3) = 0.
3. (-3) + 18.1 + 5. (-3) = -6.
5•(-3) + 12•1 + 2•(-3) = -9.
в) Решение методом Жордана-Гаусса:
Составим расширенную матрицу:

Запишем систему в виде:
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (2).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
РЭ - разрешающий элемент (2), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
|
x1 |
x2 |
x3 |
B |
|
2 / 2 = 1 |
9 / 2 = 4.5 |
1 / 2 = 0.5 |
0 / 2 = 0 |
|
|
|
|
|
|
|
|
|
|
Разрешающий элемент равен (4.5).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
|
x1 |
x2 |
x3 |
B |
|
|
|
|
|
|
0 / 4.5 = 0 |
4.5 / 4.5 = 1 |
3.5 / 4.5 = 0.78 |
-6 / 4.5 = -1.33 |
|
|
|
|
|
Разрешающий элемент равен (7.67).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
|
x1 |
x2 |
x3 |
B |
|
|
|
|
|
|
|
|
|
|
|
0 / 7.67 = 0 |
0 / 7.67 = 0 |
7.67 / 7.67 = 1 |
-23 / 7.67 = -3 |
x1 = -3, x2 = 1, x3 = -3
Проверка: 2.(-3) + 9.1 + 1.(-3) = 0.
3. (-3) + 18.1 + 5. (-3) = -6.
5•(-3) + 12•1 + 2•(-3) = -9.
Задание
3.
Векторы
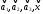 заданы
своими координатами в каноническом
базисе
заданы
своими координатами в каноническом
базисе
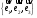 .
Требуется:
.
Требуется:
а)
показать, что система векторов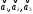 образует базис в пространстве R3.
образует базис в пространстве R3.
б)
записать матрицу перехода от канонического
базиса
 к базису
к базису
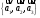 и
разложить вектор
и
разложить вектор
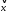 по этому базису.
по этому базису.
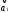 =
(3,2,2)
=
(3,2,2)
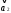 =
(2, 3, 1)
=
(2, 3, 1)
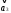 =
(1, 1, 3)
=
(1, 1, 3)
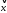 =
(5, 1, 11)
=
(5, 1, 11)
а) Система векторов
линейного пространства образует базис
в R3,
если эта система векторов упорядочена,
линейно независима и любой вектор
линейно выражается через векторы
системы. Составим матрицу из векторов
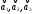 :
:
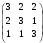
Вычислим определитель основной матрицы по третьей строке:
Δ = (2-3.2) - (1.3 – 2 .2) + 3(3*3-2*2) = -4 + 1 + 15 = 12.
Так
как определитель матрицы не равен нулю
(12 0),
то векторы
0),
то векторы
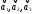 линейно
независимы и образуют базис в трехмерном
пространстве R3.
линейно
независимы и образуют базис в трехмерном
пространстве R3.
б)
Запишем матрицу перехода от канонического
базиса
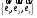 к
к
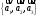 .
.

Провели следующие преобразования:
1) из 1 столбца вычли 2 столбец;
2) к 3 столбцу прибавили 1 столбец;
3) 3 столбец разделили на 3;
4) из 2 столбца вычли 3 столбец;
5) из 1 строки вычли 2 строку;
6) ко второй строке прибавили 1 строку.
7) из 2 столбца вычли 1 столбец;
8) 2 столбец разделили на 4;
Матрица перехода имеет вид:
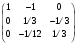
Разложим
вектор
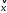 по полученному базису. Для разложения
вектора по базису запишем векторное
уравнение: с1a1
+ с2a2
+ с3a3
= х. Перепишем векторное уравнение в
матричном виде и решим его методом
Гаусса.
по полученному базису. Для разложения
вектора по базису запишем векторное
уравнение: с1a1
+ с2a2
+ с3a3
= х. Перепишем векторное уравнение в
матричном виде и решим его методом
Гаусса.
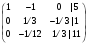
Решение СЛАУ методом Гаусса.
Запишем систему в виде расширенной матрицы:
Для удобства вычислений поменяем строки местами:
Умножим 1-ую строку на (0.249999992499). Добавим 2-ую строку к 1-ой:
Теперь исходную систему можно записать как:
x3 = 11.249999992499/0.250000000001
x2 = [11 - (0.33x3)]/(-0.08333333)
x1 = [5 - ( - x2)]/1
Из 1-ой строки выражаем x3
Из 2-ой строки выражаем x2
Из 3-ой строки выражаем x1
Ответ. х = 53a1 + 48а2 + 45 а3
Задание 4.
Элементы матрицы С4х5 заданы по вариантам заданы по вариантам:
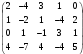
1. Считая матрицу С4х5 матрицей однородной СХ = 0, найти для этой системы
а) фундаментальную систему решений;
б) общее решение;
в) какое-нибудь частное решение.
Применяя к расширенной матрице, последовательность элементарных операций стремимся, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.
Решение СЛАУ методом Гаусса.
Запишем систему в виде расширенной матрицы:
|
2 |
-4 |
3 |
1 |
0 |
0 |
|
1 |
-2 |
1 |
-4 |
2 |
0 |
|
0 |
1 |
-1 |
3 |
1 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
0 |
Для удобства вычислений поменяем строки местами:
|
0 |
1 |
-1 |
3 |
1 |
0 |
|
1 |
-2 |
1 |
-4 |
2 |
0 |
|
2 |
-4 |
3 |
1 |
0 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
0 |
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
|
0 |
1 |
-1 |
3 |
1 |
0 |
|
0 |
0 |
-1 |
-9 |
4 |
0 |
|
2 |
-4 |
3 |
1 |
0 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
0 |
Умножим 3-ую строку на (2). Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой:
|
0 |
1 |
-1 |
3 |
1 |
0 |
|
0 |
0 |
-1 |
-9 |
4 |
0 |
|
0 |
-1 |
2 |
6 |
-5 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
0 |
Для удобства вычислений поменяем строки местами:
|
0 |
0 |
-1 |
-9 |
4 |
0 |
|
0 |
1 |
-1 |
3 |
1 |
0 |
|
0 |
-1 |
2 |
6 |
-5 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
0 |
Добавим 3-ую строку к 2-ой:
|
0 |
0 |
-1 |
-9 |
4 |
0 |
|
0 |
0 |
1 |
9 |
-4 |
0 |
|
0 |
-1 |
2 |
6 |
-5 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
0 |
Добавим 2-ую строку к 1-ой:
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
9 |
-4 |
0 |
|
0 |
-1 |
2 |
6 |
-5 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
0 |
Теперь исходную систему можно записать как:
x3 = - (9x4 - 4x5)/1
x2 = 2x3 + 6x4 - 5x5
x1 = -(- 7x2 + 4x3 - 4x4 + 5x5)/4
Необходимо переменные x4,x5 принять в качестве свободных переменных и через них выразить остальные переменные.
Окончательный
вид системы следующий:
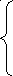
x1 = -(- 7x2 + 4x3 - 4x4 + 5x5)/4
x2 = 2x3 + 6x4 - 5x5
x3 = - (9x4 - 4x5)/1
x4, x5 - свободные переменные.
Заданная система уравнений имеет множество решений.
Подставим в качестве свободных переменных x4 и x5 число 1.
Тогда при x4 = 1, x5 = 1: x3 = -19/30, x1 = 217/30, x2 = 14/3.
Фундаментальное решение системы уравнений имеет вид:
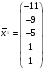
Частное решение системы уравнений при x4 = 0, x5 = 0 имеет вид:
Из 2-ой строки выражаем x3
Из 3-ой строки выражаем x2
Из 4-ой строки выражаем x1
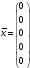
2. Считая матрицу С4х5 расширенной матрицей неоднородной системы С’’X = C’, где С = (С’’| C’), решить эту систему уравнений, предварительно исследовав ее совместность по теореме Кронекера-Капелли.

Исследуем совместность СУ по теореме Кронекера-Капелли.
Определим ранг основной матрицы:
Выпишем основную матрицу системы:
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Умножим 3-ую строку на (2). Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой:
Для удобства вычислений поменяем строки местами:
Добавим 3-ую строку к 2-ой:
В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 3.
Ответ: rang|А|=3
Определим ранг расширенной матрицы:

Выпишем основную матрицу системы:
|
2 |
-4 |
3 |
1 |
0 |
|
1 |
-2 |
1 |
-4 |
2 |
|
0 |
1 |
-1 |
3 |
1 |
|
4 |
-7 |
4 |
-4 |
5 |
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Для удобства вычислений поменяем строки местами:
|
0 |
1 |
-1 |
3 |
1 |
|
1 |
-2 |
1 |
-4 |
2 |
|
2 |
-4 |
3 |
1 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
|
0 |
1 |
-1 |
3 |
1 |
|
0 |
0 |
-1 |
-9 |
4 |
|
2 |
-4 |
3 |
1 |
0 |
|
4 |
-7 |
4 |
-4 |
5 |
Умножим 3-ую строку на (2). Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой:
|
0 |
1 |
-1 |
3 |
1 |
|
0 |
0 |
-1 |
-9 |
4 |
|
0 |
-1 |
2 |
6 |
-5 |
|
4 |
-7 |
4 |
-4 |
5 |
Для удобства вычислений поменяем строки местами:
|
0 |
0 |
-1 |
-9 |
4 |
|
0 |
1 |
-1 |
3 |
1 |
|
0 |
-1 |
2 |
6 |
-5 |
|
4 |
-7 |
4 |
-4 |
5 |
Добавим 3-ую строку к 2-ой:
|
0 |
0 |
-1 |
-9 |
4 |
|
0 |
0 |
1 |
9 |
-4 |
|
0 |
-1 |
2 |
6 |
-5 |
|
4 |
-7 |
4 |
-4 |
5 |
