11. Уравнения Пуассона-Лапласа для электро- и магнитостатического полей

11.1. Уравнения электростатического поля

• Уравнение Пуассона:

. (11.1)

Здесь учтено, что .

• Уравнение Лапласа:

. (11.2)

• Граничные условия:

(11.3)

• Граничные условия в ССК:

11.2. Уравнения магнитостатического поля

• Уравнение Пуассона:

. (11.4)

• Уравнение Лапласа:

. (11.5)

• Граничные условия:

(11.6)

• Граничные условия в ССК:

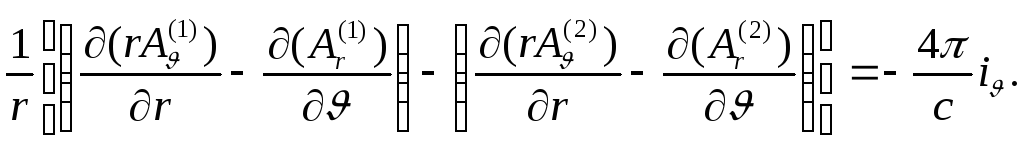
12. Электромагнитные потенциалы

• Определения скалярного и векторногопотенциалов:

, .

• Потенциалы ,и,эквивалентны, если они связаны соотношениями:

, .

• Калибровка Лоренца:

.

• Уравнения для скалярного и векторногопотенциалов:

,

.

13. Запаздывающие потенциалы

• Скалярный потенциал:

.

• Векторный потенциал:

.

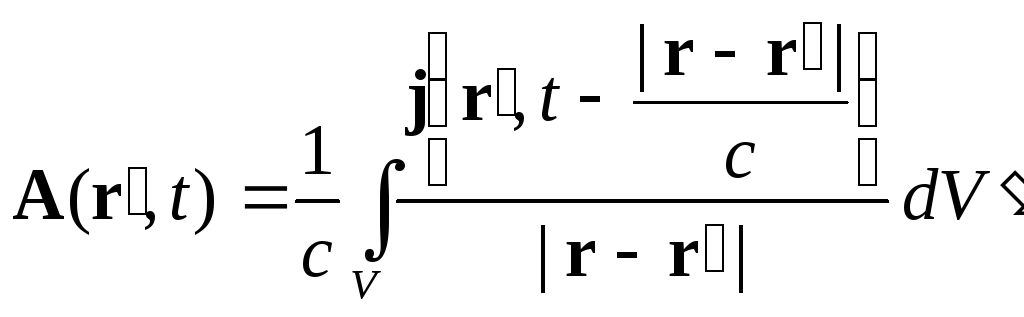ПРИЛОЖЕНИЯ

Задание 1. Найти:

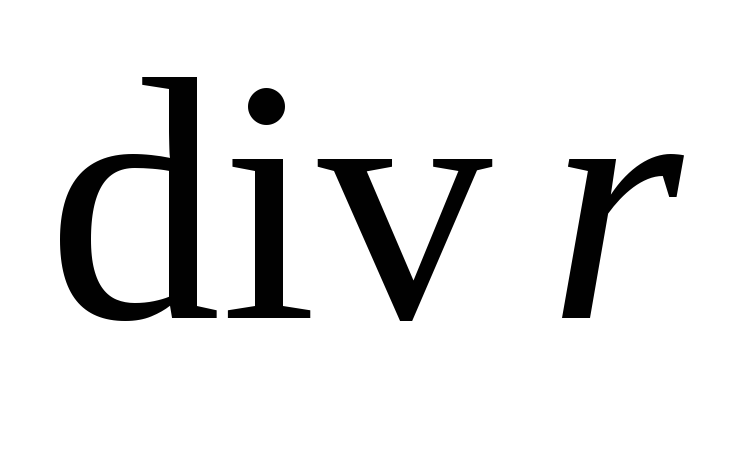1. ,,, где– модуль радиус-вектора;

2. ,,, где– радиус-вектор;

Решение.

1) В ДСК, поэтому:

.

Выражения ине имеют смысла, поскольку операции вычисления диверген-ции и ротора применяются к векторным функциям.

2) Очевидно, что

,

.

Выражение не имеет смысла, поскольку операция вычисления градиента применяется к скалярным функциям.

Задание 2. Используя Т.Г-О, найти поле однородно заряженной сферы радиуса ().

Решение.

Поле обладает сферической симметрией, поэтому

,.

Применим теорему Гаусса-Остроградского к сферической поверхности, центр которой совпадает с центром заряженной сферы. В результате находим;

,

где – заряд, находящийся в объеме, охваченном поверхностью.

Вне сферы , а потому

.

Внутри сферы . Следовательно

.

Таким образом:

Задание 3. Найти поле шара радиуса , однородно заряженного по объему (). Решить задачу тремя способами:

1. используя Т.Г-О;

2. используя уравнение Пуассона;

3. используя уравнения Максвелла.

Решение.

a) Решение с помощью теоремы Гаусса-Остроградского.

Решение задачи во многом аналогично предыдущему.

Вне шара , так что

.

Внутри шара . Поскольку, получаем. Следовательно

.

Таким образом:

(14.1)

b) Решение с помощью уравнения Пуассона.

Выделим две области:

1. Вне шара ,

2. Внутри шара ;

Вне шара объемные заряды отсутствуют, поэтому потенциал удовлетворяет уравнению Лапласа

. (14.2)

Внутри шара объемный заряд распределен с плотностью , поэтомуудовлетворяет уравнению Пуассона

. (14.3)

Границей между областями является сфера, на которой должны выполняться следующие граничные условия:

(14.4)

Поскольку распределение заряда имеет сферическую симметрию, то и

,

где – радиальная часть оператора Лапласа.

Уравнениям (14.1) и (14.2) соответствуют решения

,

.

Для определения четырех неизвестных констант мы используем 1) два граничных условия (14.3) и 2) два дополнительных условия. В качестве одного из дополнительных условий потребуем, чтобы значения приоставались ограниченными, поскольку в начале координат точечные заряды отсутствуют. Из этого следует, что. Далее, учтем, что заряд расположен в ограниченной области пространства, поэтому можно потребовать, чтобы припотенциалстремился к нулю. Отсюда получаем.

Постоянные иопределяются граничными условиями (14.3). Отсюда

,.

Итак, потенциал поля равен

(14.5)

Нетрудно убедиться, что напряженность поля совпадает с (14.1).

с) Решение с помощью уравнений Максвелла для электростатического поля.

Выделим, как и в пункте B, две области. Уравнения Максвелла (10.5) принимают:

,, для; (14.4)

,, для. (14.5)

Граничные условия для нормальной и тангенциальнойсоставляющих напряженности поля имеют вид:

(14.6)

Поскольку заряды распределены сферически симметрично, то

.

Вследствие радиальной симметрии электрического поля, уравнения для ротора его вектора напряженности в областях 1 и 2 удовлетворяются тождественно. То же самое можно сказать о граничных условиях для тангенциальных составляющих вектора напряженности. Уравнение дляследуют из уравнений для дивергенции напряженности:

.

Нетрудно видеть, что

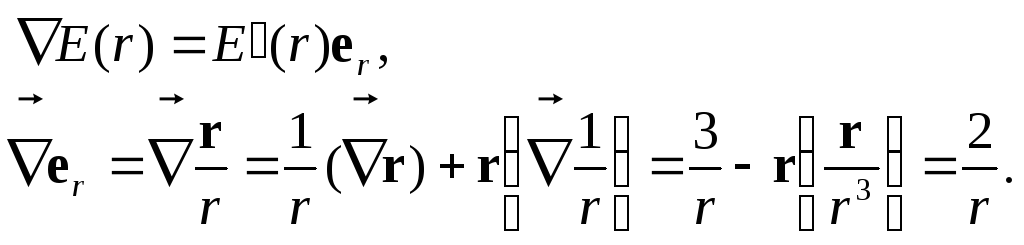
Таким образом,

,

и мы приходим к уравнениям:

Решения первого и второго уравнений имеют вид соответственно

,

.

Поскольку в начале координат нет точечных зарядов, напряженность поля при должна оставаться ограниченной. Поэтомуи

.

Из граничного условия находим, так что

.

15