
- •Список вопросов к экзамену по математическому анализу
- •2. Критерий Коши сходимости знакопостоянного ряда.
- •3. Признаки сравнения знакопостоянных рядов.
- •4. Знакопеременные ряды. Абсолютная и условная сходимость ряда.
- •5. Признаки Лейбница, Абеля и Дирихле сходимости знакопеременных рядов.
- •6. Действия над рядами. Сумма и произведение рядов.
- •7. Функциональные ряды. Область сходимости функционального ряда.
- •8. Равномерная сходимость. Мажорантный признак Вейерштрасса.
- •9. Степенные ряды. Интервал и радиус сходимости. Ряд Тейлора.
- •10. Ряд Фурье. Условие поточечной сходимости.
- •11.Ряд Фурье. Условие равномерной сходимости.
- •12.Представление функции в виде интеграла Фурье
- •13. Преобразование Фурье
- •14. Собственные интегралы, зависящие от параметра. Предельный переход под знаком интеграла.
- •15.Дифференцирование и интегрирование под знаком интеграла
- •16. Г- и в- функции Эйлера и их основные свойства.
- •17.Двойной интеграл. Теорема о среднем.
- •18. Сведение двойного интеграла к повторному.
- •19. Приложения двойного интеграла.
- •20. Замена переменных в двойном интеграле.
- •21.Тройной интеграл. Приложения тройного интеграла.
- •22.Сведение тройного интеграла к повторному.
- •23.Замена переменных в тройном интеграле.
- •24.Криволинейные интегралы первого и второго рода.
- •25.Теорема Грина.
- •26.Поверхностные интегралы первого и второго рода.
- •27.Теоремы Остроградского-Гаусса и Стокса.
- •28.Элементы теории поля. Дифференциальные векторные операции.
3. Признаки сравнения знакопостоянных рядов.
Теорема: Пусть
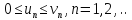 ,
тогда
,
тогда
1)Если ряд
 сходится,
то и ряд
сходится,
то и ряд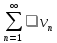 сходится;
сходится;
Если ряд
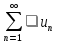 расходится,
то расходится и ряд
расходится,
то расходится и ряд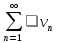 .
.
Следствие. Пусть
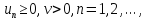 и
и .
Тогда:
.
Тогда:
Если ряд
 сходится
и
сходится
и ,
то сходится и ряд
,
то сходится и ряд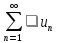 ;
;Если ряд
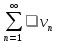 расходится
и
расходится
и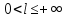 ,
то расходится и ряд
,
то расходится и ряд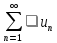 .
.
В частности, если ,
то ряды
,
то ряды и
и сходятся
и расходятся одновременно.
сходятся
и расходятся одновременно.
Доказательство теоремы: Если
ряд
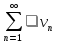 сходится,
т. е. Имеет конечную сумму
сходится,
т. е. Имеет конечную сумму ,
и
,
и ,
то для любогоn=1,2,...
выполняется неравенство
,
то для любогоn=1,2,...
выполняется неравенство .
Следовательно,
.
Следовательно,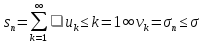 ,
а это означает, что ряд
,
а это означает, что ряд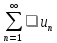 сходится.
Если ряд
сходится.
Если ряд расходится,
то и расходится и ряд
расходится,
то и расходится и ряд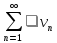 ,
так как, если бы он сходился, то в силу
уже доказанного расходился бы и ряд
,
так как, если бы он сходился, то в силу
уже доказанного расходился бы и ряд .
.
4. Знакопеременные ряды. Абсолютная и условная сходимость ряда.
Если последовательность
 убывает
и стремится к нулю, т. е.
убывает
и стремится к нулю, т. е. (1),
то ряд
(1),
то ряд сходится,
причем, если
сходится,
причем, если ,
, ,
то при любомn=1,2,...
выполняется неравенство
,
то при любомn=1,2,...
выполняется неравенство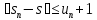 .
Из условия (1) следует, что
.
Из условия (1) следует, что ,
в силу чего члены ряда поочередно
,
в силу чего члены ряда поочередно .
Ряды вида
.
Ряды вида при
при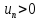 называются
знакочередующимися.
называются
знакочередующимися.
Абсолютно сходящиеся ряды:
Ряд
 ,
, называется
абсолютно сходящимся, если ряд, членами
которого являются абсолютные величины
членов данного ряда, т. е.
называется
абсолютно сходящимся, если ряд, членами
которого являются абсолютные величины
членов данного ряда, т. е. сходится.
сходится.
Критерий Коши абсолютной
сходимости ряда: Для того, чтобы ряд
абсолютно сходился, необходимо и
достаточно, чтобы для любого
 существовало
такое
существовало
такое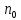 ,
что для всех номеров
,
что для всех номеров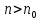 и
всех
и
всех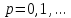 выполнялось
бы неравенство
выполнялось
бы неравенство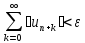 .
.
Теорема: Если ряд абсолютно сходится, то он сходится.
Доказательство:
Следует из неравенства
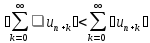 .
В самом деле, в силу критерия Коши
абсолютной сходимости ряда для любого
.
В самом деле, в силу критерия Коши
абсолютной сходимости ряда для любого существует
такое
существует
такое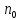 ,
что для всех
,
что для всех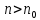 и
всех
и
всех правая
часть неравенства меньше
правая
часть неравенства меньше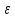 .
Следовательно, и левая часть этого
неравенства окажется меньше
.
Следовательно, и левая часть этого
неравенства окажется меньше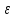 ,
т. е. для ряда
,
т. е. для ряда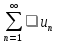 выполняется
критерий Коши сходимости рядов и потому
он сходится.
выполняется
критерий Коши сходимости рядов и потому
он сходится.
Условно сходящиеся ряды:
Сходящийся, но не абсолютно
сходящийся ряд называется условно
сходящимся рядом. Для ряда
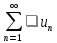 с
действительными членами обозначим
через
с
действительными членами обозначим
через и
и соответственно
его неотрицательные и отрицательные
члены, взятые в том же порядке, в котором
они расположены в ряде. Если одно из
множеств
соответственно
его неотрицательные и отрицательные
члены, взятые в том же порядке, в котором
они расположены в ряде. Если одно из
множеств или
или окажется
конечным, то, отбросив в ряде соответствующее
конечное число первых членов, получим
остаток ряда, члены которого будут
неотрицательны или неположительны и,
следовательно, во втором случае
неотрицательны после умножения всех
членов на -1. В обоих случаях, если исходный
ряд сходится, то он очевидным образом
абсолютно сходится. Таким образом, если
ряд
окажется
конечным, то, отбросив в ряде соответствующее
конечное число первых членов, получим
остаток ряда, члены которого будут
неотрицательны или неположительны и,
следовательно, во втором случае
неотрицательны после умножения всех
членов на -1. В обоих случаях, если исходный
ряд сходится, то он очевидным образом
абсолютно сходится. Таким образом, если
ряд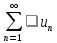 условно
сходится, то оба множества
условно
сходится, то оба множества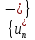 и
и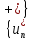 бесконечны,
т. е. являются последовательностями.
Рассмотрим ряды
бесконечны,
т. е. являются последовательностями.
Рассмотрим ряды ,
,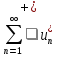 .
Согласно определению члены этих рядов
неотрицательны, поэтому, если они
расходятся, то
.
Согласно определению члены этих рядов
неотрицательны, поэтому, если они
расходятся, то ,
, .
.
Лемма: Если ряд
 условно
сходятся, то ряды
условно
сходятся, то ряды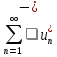 и
и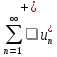 расходсятся.
расходсятся.
5. Признаки Лейбница, Абеля и Дирихле сходимости знакопеременных рядов.
Теорема (Лейбниц): Если
последовательность
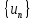 убывает
и стремится к нулю, т. е.
убывает
и стремится к нулю, т. е. (1),
то ряд
(1),
то ряд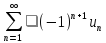 сходится,
причем, если
сходится,
причем, если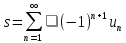 ,
, ,
то при любомn=1,2,...
выполняется неравенство
,
то при любомn=1,2,...
выполняется неравенство .
.
Лемма (Абель): Если для всех
j= 1,2,...,n-1
выполняются неравества ,
и для всехj= 1,2,...,n— неравенства
,
и для всехj= 1,2,...,n— неравенства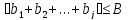 .
то
.
то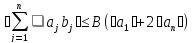 .
.
Доказательство:
 мы
воспользовались здесь равенством
мы
воспользовались здесь равенством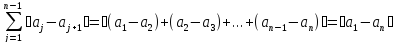 .
.
Теорема( признак Дирихле):
Если последовательность
 монотонная
и
монотонная
и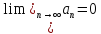 ,
а последовательность частичных сумм
ряда
,
а последовательность частичных сумм
ряда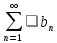 ограничена,
то ряд
ограничена,
то ряд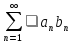 сходится.
сходится.
Доказательство: Из ограниченности
последовательности частичных сумм
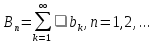 ,
ряда
,
ряда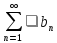 следует,
что существует такое число
следует,
что существует такое число ,
что для всехn=1,2,...
выполняются неравенства
,
что для всехn=1,2,...
выполняются неравенства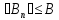 и,
следовательно, для всехn=2,3,...
и всехp=0,1,... - неравенства
и,
следовательно, для всехn=2,3,...
и всехp=0,1,... - неравенства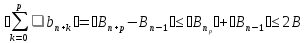 .
Зафиксируем произвольно
.
Зафиксируем произвольно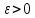 .
В силу условия существуется такой номер
.
В силу условия существуется такой номер ,
что для всех
,
что для всех имеет
место неравенство
имеет
место неравенство .
Поэтому для всех
.
Поэтому для всех и
всехp=0,1,... будем иметь
и
всехp=0,1,... будем иметь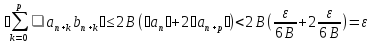 ,
т. е. ряд
,
т. е. ряд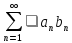 удолетворяет
критерию Коши схоидмости рядов и,
следовательно сходится.
удолетворяет
критерию Коши схоидмости рядов и,
следовательно сходится.
Теорема( признак Абеля): Если
последовательность
 ограничена
и монотонна, а ряд
ограничена
и монотонна, а ряд сходится,
то сходится и ряд
сходится,
то сходится и ряд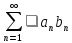 .
.
Доказательство: Из ограниченности
и монотонности последовательности
 следует
существование конечного предела
следует
существование конечного предела ,
и потому последовательность
,
и потому последовательность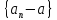 монотонная
и стремится к нулю. Из сходимости же
ряда
монотонная
и стремится к нулю. Из сходимости же
ряда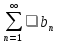 следует,
что последовательность
следует,
что последовательность его
частичных сумм
его
частичных сумм ограниченная.
Теперь имеем
ограниченная.
Теперь имеем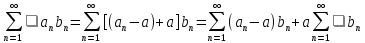 .
Второй ряд в правой части равенства
сходится по условию теоремы, а первый
— в силу признака Дирихле. Поэтому и
сходится ряд в левой части равенства.
.
Второй ряд в правой части равенства
сходится по условию теоремы, а первый
— в силу признака Дирихле. Поэтому и
сходится ряд в левой части равенства.
