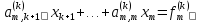Лекция 15

Простейшие численные методы

15.1. Решение системы линейных уравнений методом Гаусса

Рассмотрим численные методы решения систем линейных алгебраических уравнений

,

где А – матрица m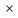m, x = (x₁, x₂,…, x_m)^T – искомый вектор, f = (f₁, f₂,…, f_m)^T – заданный вектор. Предполагается, что определитель матрицы А отличен от нуля, так что решение x существует и единственно. Для большинства вычислительных задач характерным является большой порядок матрицы А. Систему (1) можно решать по крайней мере двумя способами: или по формулам Крамера, или методом Гаусса последовательного исключения неизвестных. При больших m первый способ, основанный на вычислении определителей, требует порядка m! Арифметических действий, а метод Гаусса – только О(m³) действий. Поэтому метод Гаусса широко используется при численном решении задач линейной алгебры.

Методы численного решения системы линейных алгебраических уравнений делятся на две группы: прямые методы (Гаусса, Крамера) и итерационные методы. Итерационные методы состоят в том, что решение x системы находится как предел при n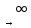последовательных приближений x⁽ⁿ⁾, где n – номер итерации. Обычно задается малое число 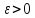и вычисления проводятся до тех пор, пока не будет выполнена оценка

.

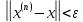Число итераций 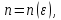которое необходимо провести для получения заданной точности, для многих методов можно найти из теоретических рассмотрений.

К решению систем линейных уравнений сводится большое количество алгоритмов задач вычислительной математики. Существует огромное количество алгоритмов решения задач линейной алгебры, большинство из которых предназначено для матриц специального вида (трехдиагональные, симметричные, ленточные, большие разреженные и т.д.).

Прямые методы не предполагают, что матрица А имеет какой-либо специальный вид и ее порядок не превышает 100.

Рассмотрим систему линейных алгебраических уравнений

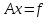, (1)

где А – матрица m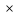m, x = (x₁, x₂,…, x_m)^T – искомый вектор, f = (f₁, f₂,…, f_m)^T – заданный вектор. Предполагается, что определитель матрицы А отличен от нуля, так что решение x существует и единственно.

Запишем систему (1) в развернутом виде

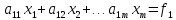
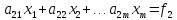(2)

…

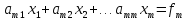
Метод Гаусса решения системы (2) состоит в последовательном исключении неизвестных x₁, x₂,…, x_m из этой системы. Предположим, что a₁₁<>0. Поделив первое уравнение на a₁₁ получим

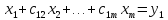, (3)

где

.

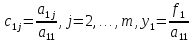Рассмотрим теперь оставшиеся уравнения системы (2):

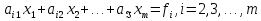. (4)

Умножим (3) на a_i1 и вычтем полученное уравнение из i-го уравнения системы (4), i=2,…,m. В результате получим следующую систему уравнений:

, , , ,

(5)

Здесь обозначено

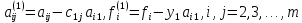. (6)

Матрица системы (5) имеет вид

.

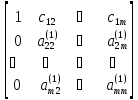Матрицы такой структуры принято обозначать так:

,

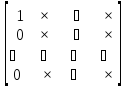Где крестиками обозначены ненулевые элементы. В системе (5) неизвестное x₁ содержится только в первом уравнении, поэтому в дальнейшем достаточно иметь дело с укороченной системой уравнений

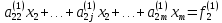, (7)

,

.

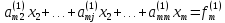Тем самым мы осуществили первый шаг метода Гаусса. Если , то из системы (7) совершенно аналогично можно исключить неизвестноеx₂ и прийти к системе, эквивалентной (2) и имеющей матрицу следующей структуры:

.

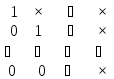При этом первое уравнение системы (5) остается без изменения.

Исключая таким же образом неизвестные x₃,x₄,…,x_m, придем окончательно к системе уравнений вида

, , , , , Матрица этой системы

(8)

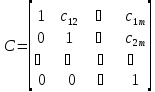. (9)

Содержит нули всюду ниже главной диагонали. Матрицы такого вида называются верхними треугольными матрицами.

Получение системы (8) составляет прямой ход метода Гаусса. Обратный ход заключается в нахождении неизвестных x₁,x₂,…,x_m из системы (8). Поскольку матрица имеет треугольный вид, можно последовательно, начиная с x_m, найти все неизвестные. Общие формулы обратного хода имеют вид

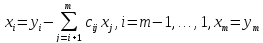. (10)

При реализации в программе прямого хода метода Гаусса нет необходимости действовать с переменными x₁,x₂,…,x_m. Достаточно указать алгоритм, согласно которому исходная матрица А преобразуется к треугольному виду (9), и указать соответствующие преобразования правых частей системы. Получим эти общие формулы. Пусть реализованы первые k-1 шагов, т.е. уже исключены переменные x₁,x₂,…,x_k-1. Тогда имеем систему

, , , , , , ,

(11)

Рассмотрим k-е уравнение этой системы

,

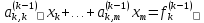И предположим, что 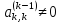. Поделив обе части этого уравнения на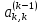, получим

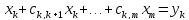, (12)

где

.

.

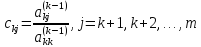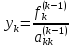Далее, умножим уравнение (12) на 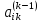и вычтем полученное соотношение изi-го уравнения системы (11), где i=k+1,k+2,…,m. В результате последняя группа уравнений системы (11) примет вид

, ,

где

.

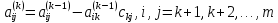
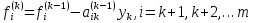Таким образом, в прямом ходе метода Гаусса коэффициенты уравнений преобразуются по следующему правилу:

,

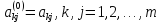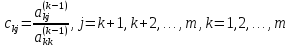. (13)

.

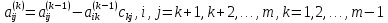Вычисление правых частей системы (8) осуществляются по формулам

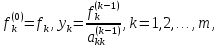(15)

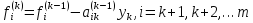. (16)

Коэффициенты c_ij и правые части y_i, i=1,2,..m, j=i+1,i+2,…, m, хранятся в памяти и используются при осуществлении обратного хода по формулам (10).

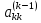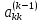Основным ограничением этого является предположение о том, что все элементы , на которые проводится деление, отличны от нуля. Числоназывается ведущим элементом наk-м шаге исключения. Даже если какой-то ведущий элемент не равен нулю, а просто близок к нему, в процессе вычислений может происходить сильное накопление погрешностей. Выход из этой ситуации заключается в том, что в качестве ведущего элемента выбирается не

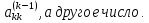
В листинге представлен метод Gauss(), который получает матрицу А и столбец свободных членов В, и реализует прямой и обратных ход метода Гаусса.

Листинг 15.1. Метод Гаусса

class Program

{

public static void Gauss(float[,] A, float[] B,

ref float[] X)

{

int Count = B.Length;

// число неизвестных = число уравнений

// решение системы: прямой ход

for (int i = 0; i <= Count - 2; i++)

// построкам

for (int j = i + 1; j <= Count-1; j++)

// постолбцам

{

for (int k=i+1; k <= Count-1; k++)

// построкам

A[k,j] += -A[i,j]*A[k,i]/A[i,i];

B[j] += -B[i]*A[i,j] / A[i, i];

}

// решение системы: обратный ход

for (int j = Count-1; j >= 0; j--)

// по столбцам

{

X[j] = B[j];

for (int k = j + 1; k <= Count-1; k++)

// по строкам

X[j] += -A[k, j] * X[k];

X[j] /= A[j, j];

}

}

Из главного модуля Main() метод Gauss() вызывается для системы

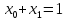
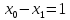
Листинг 15.2. Вызов метода Гаусса

static void Main(string[] args)

{

float [,] A = {{1,1},{1,-1}};

float[] B = { 1, 1 };

float[] X = new float[B.Length];

Gauss(A,B,ref X);

int L = X.Length;

for (int i = 0; i <= L - 1; i++)

Console.WriteLine("X[{0}] = {1}",i,X[i]);

Console.ReadKey();

}

В результате работы программы на экран выведено следующее решение:
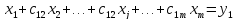
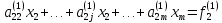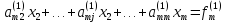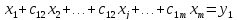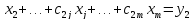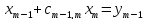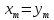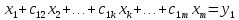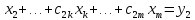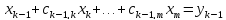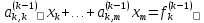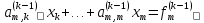
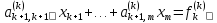