
15.2. Приближенное вычисление производных
Задача численного дифференцирования состоит в приближенном вычислении производных функции u(x) по заданным в конечном числе точек значениям этой функции. Пусть на [a,b] введена сетка:
 ,
,
И определены значения ui=u(xi) функции u(x) в точках сетки. В качестве приближенного значения u’(xi) можно взять, например, любое из следующих разностных отношений:

В качестве примера рассмотрим функцию
 ,
,
для
которой производная равна
 .
.
Код программы представлен в листинге 15.3.
Листинг 15.3. Приближенное вычисление производной
float a = 0;
float b = 3;
int m = 50;
float dx = (b - a) / m;
float x = 0, y = 0, yt = 0;
for (int i = 1; i <= m; i++)
{
x += dx;
y = (F3(x) - F3(x - dx)) / dx; // левая разность
yt = (F3(x + dx) - F3(x - dx)) / (2 * dx);
// центральная разность
g.DrawEllipse(Pens.Black,II(x)-2,JJ(y)-2, 4, 4);
g.DrawRectangle(Pens.Black,II(x)-2,JJ(yt)-2,4,4);
}
Результаты расчетов представлены на рис. 15.1.
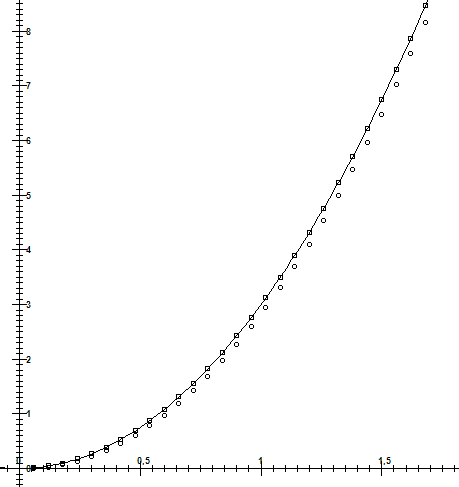
Рис. 15.1. Графики функций для расчетов
На графике видно, что производная, вычисленная через центральные разности (на рис. 15.1 изображена квадратами), хорошо совпадает с точным значением производной.
15.3. Приближенное вычисление интегралов
Рассмотрим способы приближенного вычисления определенных интегралов
 (1)
(1)
основанном на замене интеграла конечной суммой

где ck – числовые коэффициенты и xk – точки отрезка [a,b], k=0,1,…,n. Приближенное равенство
 (2)
(2)
называется квадратурной формулой, а сумма вида (2) – квадратурной суммой. Точки xk называются узлами квадратурной формулы, а числа ck - коэффициентами квадратурной формулы.
Введем на [a,b] равномерную сетку с шагом h, т.е. множество точек
 ,
,
и представим интеграл (1) в виде суммы интегралов по частичным отрезкам:
 (3)
(3)
Для построения формулы численного интегрирования на всем отрезке [a,b] достаточно построить квадратурную формулу для интеграла
 (4)
(4)
На частичном отрезке [xi-1,xi] и воспользоваться свойством (3).

Рис. 15.2. Геометрический смысл формулы прямоугольников
Формула прямоугольников. Заменим интеграл (4) выражением f(xi-1/2)h, где xi-1/2=xi-h/2. Геометрически такая замена означает, что площадь криволинейной трапеции ABCD заменяется площадью прямоугольника ABC’D’ (рис. 6). Тогда получаем формулу
 (5)
(5)
которая называется формулой прямоугольников на частичном отрезке [xi-1,xi].

Рис. 15.3. Вычисление интеграла по формуле прямоугольников
Суммируя равенства (5) по I от 1 до N, получаем составную формулу прямоугольников
 (6)
(6)
Формула трапеций. На частичном отрезке эта формула имеет вид
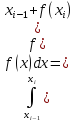 (7)
(7)
И получается путем замены подынтегральной функции f(x) интерполяционным многочленом первой степени, построенным по узлам xi-1,xi, то есть функцией


Рис. 15.4. Вычисление интеграла по формуле трапеций
Составная формула трапеций имеет вид
 (8)
(8)
где
 .
.
Формула Симпсона. При аппроксимации интеграла (4) заменим функцию f(x) параболой, проходящей через точки (xj,f(xj)), j=i-1,i-0,5,i, т.е. представим приближенно f(x) в виде

Где
 - интерполяционный многочлен Лагранжа
второй степени,
- интерполяционный многочлен Лагранжа
второй степени,
 (9)
(9)
Проводя интегрирование, получим

Таким образом, приходим к приближенному равенству
 ,
,
которое называется формулой Симпсона или формулой парабол.

Рис. 15.5. Вычисление интеграла по формулам Симпсона
На всем отрезке [a,b] формула Симпсона имеет вид
 .
.
Чтобы не использовать дробных индексов, можно обозначить

и записать формулу Симпсона в виде
 .
(10)
.
(10)
Все три приближенные способа представлены процедурами MethodRectangle(), MethodTrapezes() и MethodSimpson() в следующем листинге:
Листинг 15.4. Приближенное вычисление интеграла
static float F(float x)
{
return 3 * x * x;
}
static float F1(float x)
{
return x * x * x;
}
static float MethodRectangle(float a, float b)
{
int n = 200;
float dx = (b - a) / n;
float result = 0;
for (int i = 1; i <= n; i++)
result += dx * F(a+i*dx);
return result;
}
static float MethodTrapezes(float a, float b)
{
int n = 200;
float dx = (b - a) / n;
float result = (F(a)+F(b))*dx/2;
for (int i = 1+1; i <= n-1; i++)
result += dx * F(a + i * dx);
return result;
}
static float MethodSimpson(float a, float b)
{
int n = 200;
float dx = (b - a) / n;
int[] k = new int[] { 2, 4 };
float result = (F(a) + F(b)) * dx / 3;
for (int i = 1 + 1; i <= n - 1; i++)
result += k[i % 2]*dx*F(a + i * dx)/3;
return result;
}
static void Main(string[] args)
{
float a = 0;
float b = 1;
Console.WriteLine("Точное={0}",F1(b)-F1(a));
float s = MethodRectangle(a, b);
Console.WriteLine("Метод прямоугольников");
Console.WriteLine("s = {0}", s);
Console.WriteLine("");
s = MethodTrapezes(a, b);
Console.WriteLine("Метод трапеций");
Console.WriteLine("s = {0}", s);
Console.WriteLine("");
s = MethodSimpson(a, b);
Console.WriteLine("Метод Симпсона");
Console.WriteLine("s = {0}", s);
Console.WriteLine("");
Console.ReadKey();
}
В качестве примера рассмотрим определенный интеграл:
 .
.
Полученные результаты показывают следующее:

