Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

434	yehuda haas and shmuel zilberg

VI. Examples

A.Loops in Molecular Photochemistry: Qualitative Discussion

1.Four-Electron Problems

2.More Than Four Electrons

B.A Quantitative Example: The Photochemistry of 1,4-Cyclohexadiene (CHDN) VII. Comparison with Other Methods for Locating Conical Intersections

VIII. Impact on Molecular Photochemistry and Future Outlook

Appendix A: Phase Inverting Reactions

I. The Model

Acknowledgments

References

I.INTRODUCTION

Conical intersections, introduced over 60 years ago as possible efficient funnels connecting different electronically excited states [1], are now generally believed to be involved in many photochemical reactions. Direct laboratory observation of these subsurfaces on the potential surfaces of polyatomic molecules is difficult, since they are not stationary ‘‘points’’. The system is expected to pass through them very rapidly, as the transition from one electronic state to another at the conical intersection is very rapid. Their presence is surmised from the following data [2–5]:

Very rapid (subpicosecond) decay of electronically excited states.

Lack of fluorescence.

Rapid formation of ground-state products.

In recent years, computational testimonies for the existence of conical intersections in many polyatomic systems became abundant and compelling [6–11]. The current consensus concerning the ubiquitous presence of conical intersections in polyatomic molecules is due in large part to computational ‘‘experiments.’’

In this chapter, we present an analysis of conical intersections, based on chemical reaction concepts. It is argued that conical intersections leading to the ground state can be identified and characterized by considering properties of the ground-state surface only. The basis of the model is the Longuet-Higgins phase-change rule [12,13] (Section II), which provides a simple criterion for the existence of a degeneracy on the electronic ground state. Longuet-Higgins showed that a degeneracy necessarily exists within a region enclosed by a loop, if the total electronic wave function changes sign upon being transported around the loop. (For more details, see Section II). We propose to construct the loop discussed by Longuet-Higgins from reaction coordinates of elementary reactions converting the reactant to the desired product and other possible

conical intersections in molecular photochemistry

435

products. In this sense, our approach is ‘‘chemical’’ in nature. In order to properly search for the elementary reactions, the need for an agreed definition of common terms such as a molecule and a transition state arises. This reaction is carried out in this section, based on the concept of electron spin pairing [14,15]. The reacting system (reactant and product) are treated as a two-state system [16]. The spirit of this strategy is akin to the Evans–Dewar–Zimmerman approach [17–21], and is closely related to the concept of aromaticity and antiaromaticity, which is dealt with in Section III.

The phase change of the total polyelectronic wave function in a chemical reaction [22–25], which is more extensively discussed in Section III, is central to the approach presented in this chapter. It is shown that some reactions may be classified as phase preserving (p) on the ground-state surface, while others are phase inverting (i). The distinction between the two can be made by checking the change in the spin pairing of the electrons that are exchanged in the reaction. A complete loop around a point in configuration space may be constructed using a number of consecutive elementary reactions, starting and ending with the reactant A. The smallest possible loop typically requires at least three reactions: two other molecules must be involved in order to complete a loop; they are the desired product B and another one C, so that the complete loop is A ! B ! C ! A. Two types of phase inverting loops may be constructed: those in which each reaction is phase inverting (an i3 loop) and those in which one reaction is phase inverting, and the other two phase preserving (an ip2 loop). At least one reaction must be phase inverting for the complete loop to be phase inverting and thus to encircle a conical intersection and lead to a photochemical reaction. It follows, that if a conical intersection is crossed during a photochemical reaction, in general at least two products are expected, B and C. A single product requires the existence of a two-component loop. This is possible if one of the molecules may be viewed as the out-of-phase combination of a twostate system. The allyl radical (Section IV, cf. Fig. 12) and the triplet state are examples of such systems. We restrict the discussion in this chapter to singlet states only.

In Section IV, the construction of phase inverting loops is described. A conical intersection is an example of an electronic degeneracy; A well-known case of electronic degeneracy in polyatomic molecules occurs in the Jahn–Teller effect. Systems of high symmetry tend to distort to lower symmetry if their electronic ground state is degenerate. We show (Section V) that the LonguetHiggins loop treatment can be applied to these systems, making them part of the general conical intersections concept.

The method discussed in this chapter allows, in principle, the detection of all conical intersections connecting the ground with the excited state. Assuming that photochemical products are mainly formed through conical intersections, it therefore provides a means to design selection rules for photochemistry.

436	yehuda haas and shmuel zilberg

A.A Chemical Reaction as a Two-State System

The concept of two-state systems occupies a central role in quantum mechanics [16,26]. As discussed extensively by Feynmann et al. [16], benzene and ammonia are examples of simple two-state systems: Their properties are best described by assuming that the wave function that represents them is a combination of two base states. In the cases of ammonia and benzene, the two base states are equivalent. The two base states necessarily give rise to two independent states, which we named twin states [27,28]. One of them is the ground state, the other an excited states. The twin states are the ones observed experimentally.

The extra stabilization of benzene in the ground state, as compared to a single Kekule´ structure, is assigned to a resonance between the two equivalent base states. In standard textbooks, the fact that the combination is in-phase (i.e., that the two Kekule´ structures in the ground-state combination carry the same sign) is taken for granted. In Section III, it is shown that whether the ground state is representing by the in-phase or out-of-phase combination of the two states is determined by the permutational symmetry of the electronic wave function, and may be traced to Pauli’s principle. Hu¨ckel’s 4n þ 2 rule [29] arises from the fact that there is an odd number of electron pairs in this system.

Stabilizing resonances also occur in other systems. Some well-known ones are the allyl radical and square cyclobutadiene. It has been shown that in these cases, the ground-state wave function is constructed from the out-of-phase combination of the two components [24,30]. In Section III, it is shown that this is also a necessary result of Pauli’s principle and the permutational symmetry of the polyelectronic wave function: When the number of electron pairs exchanged in a two-state system is even, the ground state is the out-of-phase combination [28]. Three electrons may be considered as two electron pairs, one of which is half-populated. When both electron pairs are fully populated, an antiaromatic system arises (Section III).

During a chemical reaction, a chemical system (or substance) A is converted to another, B. Viewed from a quantum chemical point of view, A and B together are a single system that evolves with time. It may be approximated by a combination of two states, A at time zero and B as time approaches infinity. The first is represented by the wave function jAi and the second by jBi. At any time during the reaction, the system may be described by a combination of the two

jRiðtÞ ¼ cAðtÞjAi þ cBðtÞjBi ð1Þ

where cAðt ¼ 0Þ ¼ 1; cBðt ¼ 0Þ ¼ 0; cAðt ¼ 1Þ ¼ 0; cBðt ¼ 1Þ ¼ 1:

Within the Born–Oppenheimer (BO) approximation, jAi and jBi may be written as the product of an electronic wave function, jMiel and a nuclear wave

function jMin.
jMi ¼ jMieljMin ðM ¼ A; BÞ	ð2Þ

conical intersections in molecular photochemistry

437

It is useful to represent the polyelectronic wave function of a compound by a valence bond (VB) structure that represents the bonding between the atoms. Frequently, a single VB structure suffices, sometimes it is necessary to use several. We assume for simplicity that a single VB structure provides a faithful representation. A common way to write down a VB structure is by the spinpaired determinant, that ensures the compliance with Pauli’s principle: (It is assumed that there are 2n paired electrons in the system)

jAiel ¼ Xp	Ep P1ð1Þ2ð2Þ 2nð2nÞ½að1Þbð2Þ bð1Það2Þ&½að3Þbð4Þ
bð3Það4Þ& ½að2n 1Þbð2nÞ bð2n 1Það2nÞ&		ð3Þ

Where the summation is over all 2n! permutations P each with parity Ep. We use a short-hand notation:

jAiel ¼ ð12 12Þð34 34Þ ð2n 12n 2n 12nÞ

ð4Þ

As the electronic and nuclear wave functions are separated in the BO approximation, a single electronic wave function may be associated with many different nuclear configurations. Furthermore, the electronic energy of the system depends parametrically on the nuclear configuration fQg. It is convenient to introduce a term for all systems having a specific spin-pairing scheme, independent of the nuclear configuration. We use the term anchor to represent this group of systems.

We may now distinguish two classes of reactions:

1.The system does not change the spin-pairing scheme during the process.

In this case, jAiel remains put throughout the reaction, and only the internuclear distances or angles change. Such transformations are called

intraanchor reactions.

2.The spin-pairing scheme of the product, jBiel, is different from that of the reactant. This happens if at least two pairs of electrons have exchanged partners. In other words, at least three electrons need to be involved.

If the reaction is elementary, there is only a single transition state between A and B. At this point the derivative of the total electronic wave function with respect to the reaction coordinate QA!B vanishes:

qjRiel;TS=qQA!B ¼ 0

ð5Þ

In the transition state region, the spin-pairing change must take place. At this nuclear configuration, the electronic wave function may be written as

jRiel;TS ¼ kAjAiel þ kBjBiel

ð6Þ

438	yehuda haas and shmuel zilberg

If the sign of kA is equal to that of kB, the reaction is phase preserving, if the signs are different, the reaction is phase inverting.

We shall assume, for simplifying the notation, that the k values are positive. For a phase-inverting reaction, the wave function of the transition state is therefore written as

jRiel;TS ¼ kAjAiel kBjBiel

ðphase invertingÞ

ð7Þ

It is important to recall, that the reaction takes place on the ground-state surface. Clearly, at the same nuclear configuration, the other combination

jRiel;TS ¼ kAjAiel þ kBjBiel

ðphase preservingÞ

ð8Þ

lies on an excited state surface.

The distinction between an in-phase and an out-of-phase combination of the two base states is easy for degenerate two-state systems (such that the two components are equivalent). In these cases, the transition state has an additional symmetry element not present in either of the two base states. In other words, it belongs to a group of higher symmetry. The electronic wave function at the transition state nuclear configuration transforms as the totally symmetric representation of the new group if the transition state is the in-phase combination. If it is the out-of-phase combination, it transforms as one of the nontotally symmetric representations. In this case, the motion along the reaction coordinate is antisymmetric with respect to the new symmetry element [28]. For example, the ground state of the C2v allyl radical transforms as B1 (not A2), and the ground state of square cyclobutadiene (D4h symmetry) as B1g (not A1g). The symmetry properties of the transition states are more easily established using the VB approximation than the molecular orbital–configuration interaction (MO–CI) one. The character of the bonding before and after the reaction does not matter: The transfer of electrons from one atom to another to form a covalent, ionic, or coordinate bond is always accompanied by a change in spin pairing [31,32], and is clearly represented by the VB structures. The MO–CI method can also be used successfully, but several configurations are ordinarily required in the general case, as shown, for example, in [33].

By using the determinant form of the electronic wave functions, it is readily shown that a phase-inverting reaction is one in which an even number of electron pairs are exchanged, while in a phase-preserving reaction, an odd number of electron pairs are exchanged. This holds for Hu¨ckel-type reactions, and is demonstrated in Appendix A. For a definition of Hu¨ckel and Mo¨bius-type reactions, see Section III.

conical intersections in molecular photochemistry

439

B.Anchors

Intuitively, a molecule is defined as an assembly of atoms bound by chemical bonds, which lies in a local minimum on the potential surface. The molecule preserves its identity when the nuclei are transported from their minimum energy position, as long as the gradient of the electronic energy with respect to the displacement maintains its sign. As soon as this gradient changes its sign, the system undergoes a chemical change in an elementary reaction. The idea that a molecule is defined by the spin-pairing arrangement of the valence electrons seems to be at odds with this concept of a molecule. In particular, a definite structure is not assumed.

An anchor, as defined above, contains stable molecules, conformers, all pairs of radicals and biradicals formed by a simple bond fission in which no spin re-pairing took place, ionic species, and so on. Figure 1 shows some examples of species belonging to the same anchor. Thus, an anchor is a more general and convenient term used in the discussion of spin re-pairing.

C.Anchors, Molecules and Independent Quantum Species

At this point, it is instructive to discuss the distinction between molecules, anchors, and quantum mechanical wave functions that represent them. The topic is best introduced by using an example. Consider the H4 system [34].

1. Hydrogen molecule anchor					2. Bicyclobutane anchor
						2		H
							2	3
H		H	H H
				1	3	4 b	1	4
						a		b

a	H
Single-bond fission

3. Butadiene anchor

1	1
2	2
3	3
4	4

s-cis s-trans

Two conformers

4. Twisted ethylene anchor

H	1,2		2	H
			H 1
H	3		3,4
		4	H
H		H	H
	I		II

The conversion from I to II is by the transfer of a proton from one carbon atom to the other. No change in spin pairing.

Figure 1. Examples of species residing in the same anchor.

440	yehuda haas and shmuel zilberg
				TS(II-III)
		1			1	1
	2		3	4	3	4			2
		4			2	3
		H(III)					H(II)
				1		1
	TS(III-I) 4			2	3	2 TS(I-II)
				3		4
					1
				4	3
Figure 2. The H4 system. TS are transition					2
					H(I)
states.

The most stable nuclear configuration of this system is a pair of H2 molecules. There are three possible spin coupling combinations for H4 corresponding to three distinct stable product H2 pairs: H1:H2 with H3:H4, H1:H3 with H2:H4, and H1:H4 with H2:H3. Each H atom contributes one electron, the dot diagrams indicate spin pairing. The three combinations are designated as H(I), H(II), and H(III), respectively. They may be interconverted via square transition states, Figure 2.

The electronic wave functions of the different spin-paired systems are not necessarily linearly independent. Writing out the VB wave function shows that one of them may be expressed as a linear combination of the other two.

Nevertheless, each of them is obviously a separate chemical entity, that can be clearly distinguished from the other two. [This is readily checked by considering a hypothetical system containing four isotopic H atoms (H, D, T, and U). The anchors will be HD þ TU, HT þ DU, and HU þ DT].

In short-hand notation, the electronic wave functions of the three spin-paired combinations may be written as

jHðIÞi ¼ ð12

12Þð34

34Þ ¼ 1234 1234 1234 þ 1234

ð9aÞ

ð9bÞ

jHðIIÞi ¼ ð13

13Þð24

24Þ ¼ 1324 1324 1324 þ 1324

ð9cÞ

jHðIIIÞi ¼ ð14

14Þð23

23Þ ¼ 1423 1423 1423 þ 1424

Since exchanging two columns in a determinant changes its sign, simple algebra shows that

jHðIIIÞi ¼ jHðIÞi þ jHðIIÞi

ð10Þ

Thus, the electronic wave function of H(III) is (to within a multiplication constant) equal to the in-phase combination of the electronic wave functions of

conical intersections in molecular photochemistry

441

H(I) and H(II). This fact does not provide any information on the nuclear structure of this species at the energy minimum. By symmetry, it is clear that the system has three equivalent minima on the ground-state surface, which were designated as the three diatomic pairs. The nuclear geometry of each of these minima is quite different from that of the other two.

There are two nuclear configurations on the ground-state surface that are of special interest to the chemist: One is the energy minimum for the in-phase combination of jHðIÞi and jHðIIÞi, which is the equilibrium geometry of H(III). The second is also a stationary point on the ground-state surface, but for the out- of-phase combination of jHðIÞi and jHðIIÞi—it is the TS between H(I) and H(II). Clearly, the geometries (nuclear configuration) of these two species are quite different. Each of these structures is constructed from two base functions, and is therefore a two-state system. As for any two-state system, each has a twin state on the electronic excited surface. Thus, the in-phase combination of the two electronic wave functions jHðIÞi and jHðIIÞi at the nuclear configuration of the transition state is found on the excited-state potential surface. Likewise, the out-of-phase combination at the nuclear geometry of the minimum energy of jHðIIIÞi also lies on the excited-state potential. Thus a given spin-paired scheme of the H4 system is seen to support very different nuclear geometries on the each potential surfaces.

We can now proceed to discuss the phase-change rule and its use to locate conical intersections.

II. THE PHASE-CHANGE RULE AND THE

CONSTRUCTION OF LOOPS

Herzberg and Longuet-Higgins noted the singular behavior of the electronic wave function around a degeneracy [12,13]. This observation is the basis of the present approach to molecular photochemistry. Let fðr; RÞ be the total polyelectronic wave function of a polyatomic molecule, where r and R denote the electronic and nuclear coordinates, respectively. Within the BO approximation, this wave function is an explicit function of r for a given set of nuclear coordinates R0. It must be continuous everywhere in the electronic coordinates r, but may change sign in an abrupt, seemingly discontinuous manner when the R’s are slightly changed. If fðr; RÞ is nondegenerate throughout a certain region of the nuclear configuration space, it will be a real continuous function of the R’s as well as of the r’s. If it changes abruptly at some point, there must be two electronic states with the same energy at this point, in other words the function is degenerate at that point.

Consider the function at a certain set of R’s, R0, where fðr; RÞ is nondegenerate. When the nuclei move away from that point, and approach it back via a different route, the wave function must return to its original value. However, in

442	yehuda haas and shmuel zilberg

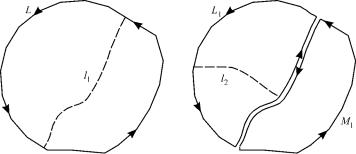
Figure 3. Longuet-Higgins’ rule proof.

the process it may change sign, since if fðr; R0Þ is a solution of the electronic wave, so is fðr; R0Þ. Thus one can distinguish two kinds of paths leading by a closed loop from R0 back to itself: sign preserving and sign reversing.

Longuet-Higgins stated and proved the following theorem [13]:

Let S be any simply connected surface in nuclear configuration space, bounded by a closed-loop L. Then, if fðr; RÞ changes sign when transported adiabatically round L, there must be at least one point on S at which fðr; RÞ is discontinuous, implying that its potential energy surface intersects that of another electronic state.

The proof was by reduction ad absurdum.

Let l1 be any line in S that bisects the area enclosed by L, and let L1 and M1 be the two loops created (Fig. 3). If L is sign reversing and if fðr; RÞ is continuous everywhere on S, than either L1 or M1 must be sign reversing. If L1 and M1 were both sign reversing or sign preserving, than L would also be sign preserving, in contradiction with the assumption. Let L1 be the sign reversing loop. It encloses a simply connected surface S1 which is smaller than S. We now bisect S1 by a line l2 and repeat the argument. In this fashion, a large number of successively smaller loops are created, all of them sign reversing. These loops converge to a point P on the surface, where fðr; RÞ is discontinuous in R, because of the sign change. Thus, the function cannot be single valued—it must be degenerate. In other words, two potential surfaces cross at this point. LonguetHiggins’ proof assumed that the electronic wave function is real everywhere. Stone [35] showed that the theorem applies also for a general phase change. Thus, when the nuclei return to their original configuration R0, the wave function may undergo a change phase Z ¼ ei , since if fðr; R0Þ is a solution of the electronic wave equation, so is ei fðr; R0Þ.

The proof runs analogously to the original Longuet-Higgins one, and is not reproduced here.

conical intersections in molecular photochemistry

443

A.Construction of Loops: Nature of the Coordinates

Herzberg and Longuet-Higgins [12] explicitly discussed the H3 system. This is a three-electron problems, which has the same spin-pairing properties as the fourelectron system H4. The loop is constructed by considering the three possible spin-pairing options for these systems (Fig. 4), compare Figure 2. The transition states for the H3 system are linear [36] and their wave functions are the out-of- phase combination of the two wave functions of the reactant and product systems. As mentioned above for H4, Pauli’s principle and the permutational symmetry of the polyelectronic wave function are the ultimate reason for the fact that the ground-state surface in this case is the out-of-phase combination, rather than the in-phase one.

Generalizing on [12], we construct a loop by using a sequence of three elementary reactions. It is emphasized that the reactions comprising the loop must be elementary ones: There should not be any other spin pairing combination that connects two anchors. This ensures that the loop in question is indeed the ‘‘smallest’’ possible one. Inspection of the loops depicted in Figure 4 shows that the H3 and H4 systems are entirely analogous. We include the H3 system in order to introduce the coordinates spanning the plane in which the loop lies, and as a prototype of all three-electron systems.

There are two independent coordinates that define the plane of a loop. If the loop is phase inverting, one of these coordinates must be phase inverting, the other, phase preserving. Out of the infinite number of possible candidates, a convenient choice are reaction coordinates (Section I). Any one of the three reaction coordinates connecting two of the anchors can be used for the

Figure 4. The H3 and H4 loops. At the center, the conical intersections are shown schematically: an equilateral triangle for H3 and a perfect tetrahedron for H4, Qp, and Qi are the phase-preserving and phase-inverting coordinates, respectively.