3.2 Типовые звенья сау

По динамическим свойствам независимо от физической природы простейшие (неделимые) звенья подразделяются на усилительные (масштабные), апериодические, интегрирующие, дифференцирующие, ко­лебательные, звенья чистого запаздывания. На эти звенья можно разложить систему любой сложности, а также синтезировать из них желаемую систему любой сложности.

Основными характеристиками звеньев являются: дифференциальное уравнение, передаточная и переходная функции, амплитудно-фазовая характеристика

Усилительные звенья

Особенностью усилительных звеньев является их практическая безынеционность, т.е. выходная величина в точности воспроизводит входную в измененном масштабе (усилители, потенциометры, редукторы, рычаги и т.д.):

, (3.4)

где - коэффициент усиления, который может быть больше и меньше единицы и иметь размерность, согласующую выходную и входную величины.

В операторной форме (3.4) запишем так:

.

Передаточная функция усилительного звена:

.

Амплитудно-фазовая характеристика

не зависит от частоты.

На комплексной плоскости представляем точку на положительной вещественной оси, удаленную от начала координат за величину .

Если на вход звена подается ступенчатый единичный сигнал, то на выходе получается переходная функция в виде ступенчатого сигнала величины .

Апериодическое звено

Его называют инерционным звеном первого порядка, одноёмкостным статическим звеном. Дифференциальное уравнение его запишем так:

, (3.5)

где - постоянная времени, имеющая размерность времени, -коэффициент усиления.

В операторной форме (3.5) запишем так (при нулевых начальных условиях):

. (3.6)

Передаточная функция звена будет такой:

. (3.7)

Если , т.е. , то

, откуда .

Используя метод неопределенных коэффициентов, получаем:

.

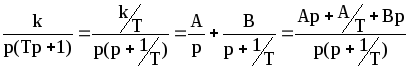Приравняв коэффициенты числителя при одинаковых степенях , получаем:

; .

Отсюда ; и

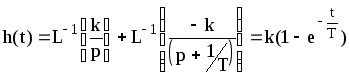. (3.8)

Сделав в передаточной функции (3.7) замену , получим:

. (3.9)

(3.10)

где - амплитудно-частотная характеристика.

Фазо-частотная характеристика .

(3.11)

АФХ апериодического звена представляет окружность с центром на вещественной оси на расстоянии и радиусом . Действительно, , .

Отсюда . Это выражение можно записать так: .

Оно представляет окружность радиусом с центром на вещественной положительной оси на расстоянии от начала координат (рисунок 3.1).

Интегрирующее звено

Выходная величина интегрирующего звена равна интегралу по времени от входной, , или . (3.12)

В операторной форме выражение (3.12) запишем так:

, передаточная Функция звена равна:

; . (3.13)

Решение уравнения (3.12) при нулевых начальных условиях и при единич­ном входном воздействии имеет вид:

, или , (3.14)

где - постоянная времени интегрирования, численно равна време­ни, через которое значение выходной величины станет равно входному воздействию (рисунок 3.2).

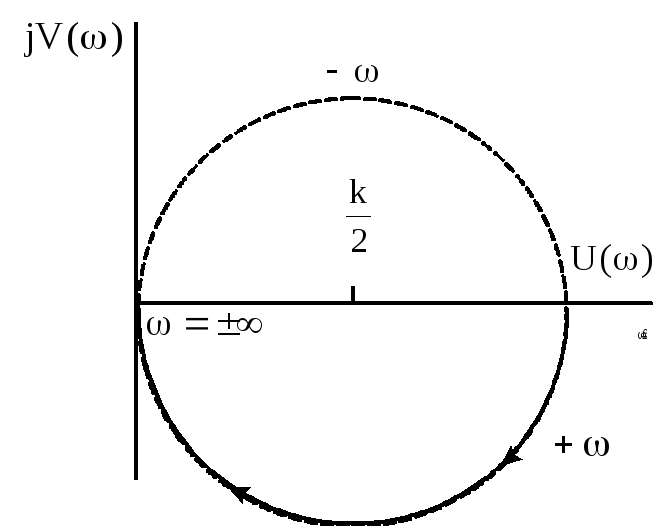
Рисунок 3.1 - АФХ апериодического звена

Амплитудно-Фазовая характеристика интегрирующего звена по­лучается из уравнения (3.12) заменой :

. (3.15)

Очевидно, что АФХ интегрирующего звена совпадает с мнимой осью комплексной плоскости, начинаясь в при и стремясь к нулю при .

Рисунок 3.2 - Иллюстрация постоянной времени идеального интегрирующего звена

Примерами интегрирующих звеньев могут служить гидравлический сервомотор, электрический двигатель постоянного тока, если выходной величиной является угол поворота, одноёмкостный объект без саморегулирования.

Дифференцирующее звено

Для идеального (физически не реализуемого) дифференцирующего звена выходная величина пропорциональна скорости изменения входной

, (3.16)

где - постоянная времени дифференцирования.

Переходная функция дифференцирующего звена представляет бесконечно большой амплитуды и бесконечно малой длительности импульс, площадь которого равна .

,

где 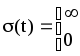при .

Передаточная и амплитудно-фазовая характеристики дифференцирующего звена получаются из выражения (3.16) и равны:

; . (3.17)

Легко видеть, что АФХ дифференцирующего звена совпадает с мнимой осью. Она начинается в начале координат при и устремляется в верхнюю полуплоскость при .

Колебательное звено

Статические и динамические свойства колебательного звена описываются дифференциальным уравнением второго порядка вида

, (3.18)

где , - постоянные времени, имеющие размерность времени. В операторном виде уравнение (3.18) запишем так:

, (3.19)

откуда передаточная функция

. (3.20)

Для получения переходной функции, рисунок 3.3, необходимо решить уравнение (3.19) при единичном входном воздействии. При этом решение будет зависеть от вида свободной составляющей, определяемой корням характеристического уравнения

, (3.21)

где .

Звено будет колебательным, если корни комплексно сопряженные, т.е. когда , где ; . (3.22)

Пусть , тогда [2]:

, ,

Переходная функция колебательного звена показана на рисунок 3.3.

.

Рисунок 3.3 – Переходная функция колебательного звена

Мнимая часть корней является круговой частотой колебаний, , где - период колебаний. Оценку переходного процесса в колебательном звене производят по степени затухания:

.

Степень затухания тем больше, чем больше отношение , и равна единице при . Если , то , при этом , и переходная функция принимает вид:

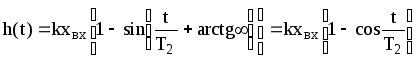. (3.23)

Амплитудно-фазовая характеристика колебательного звена, рисунок 3.4, получается из выражения (3.21) заменой :

,

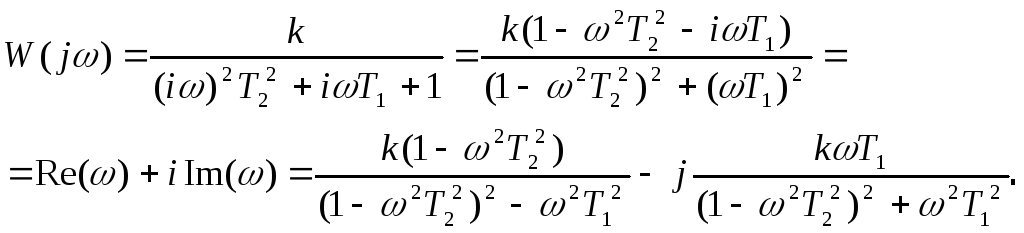
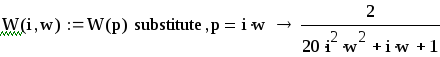
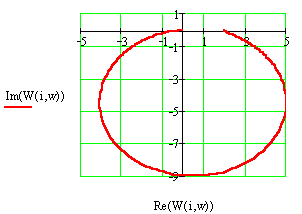
Рисунок 3.4 – Амплитудно-фазовая характеристика колебательного звена

Если корни характеристического уравнения вещественные отрицательные, то передаточную функцию (3.21) можно записать так:

. (3.24)

Это эквивалентно включению последовательно двух апериодических звеньев.

Звено чистого запаздывания

Уравнение, связывающее выходную и входную величины:

. (3.25)

Передаточная функция звена

. (3.26)

Амплитудно-фазовая характеристик

. (3.27)

АФХ представляет на комплексной плоскости окружность единичного радиуса с центром в начале координат.