ivchenko_bookreg

τp(E)

|Vk(ik) |2(1 − cos θ)δ(Ek − E) ,

1

		4.3	Intrasubband Optical Transitions					191
		η =	ω		W			(4.44)
			I
can be expressed in terms of current and field, and be written as
η =	2	Re ,j (ω) · E (ω)'			=	4πe2N2Dγ		(4.45)
							.
	I					m cnω (ω2 + γ2)

Here W is the photon absorption rate and I = (cnω /2π)|E (ω)|2 is the light intensity.

¯
For ω E, the expression for η can be derived by solving the kinetic
equation		δfk(ω)
−iω δfk(ω) +	e
	E · kf 0(Ek) +	τp	= 0

for the deviation of the electron distribution function, δfk, induced by the in-plane electric field. The result coincides with (4.45) if γ−1 is set equal to the momentum scattering time.

In the limit ω τp−1 the absorption rate W (or absorbance η) can be calculated by using Fermi’s golden rule for indirect transitions. For scattering by static defects this rule reads

W =

2π 2πe2I 2

R(i)

2

(fk0

fk0 )δ(Ek

Ek

ω)

(4.46)

ω2cnω S

|

|

−

−

−

k k

k k

i

with the second-order matrix element for defect-assisted electron-photon interaction being

R(i)	=	(e · vk )Vk(ik)						+	Vk(ik) (e · vk)
k k		Ek			−	Ek			ω
									−
	=	Vk(ik)
							e · (k − k) .			(4.47)
		m			ω

Here vk = k/m is the electron velocity, Vk(ik) is the matrix element of spin-conserving elastic scattering k → k and the index i enumerates the elementary scatterers. The corresponding momentum relaxation time that determines the mobility is given by

2π 2 = S k i

where θ is the scattering angle. Further analysis is readily performed assuming Vk(ik) is k and k independent which is valid for defects with a short-range inplane scattering potential. Then the absorbance in the high-frequency limit can be presented as

	η =	4πe2N2D γ(ω)	,	(4.48)
		m cnω ω2

192 4 Intraband Optical Spectroscopy of Nanostructures

where γ is a function of the light frequency. In accordance with the kinetic-

¯

theory result, at low frequencies, i.e. for ω E, the damping γ coincides

−1 ¯

with τp , while in the high-frequency region, ω E but ω < E21, the damping constant becomes (2τp)−1.

For intrasubband optical transitions assisted by phonons, the transition

probability rate is similar to (4.46)

W =

2π 2πe2I 2

Rk k(q) 2

δ(Ek Ek ω Ωq )

(4.49)

|

|

− − ±

ω2cnω S

k k q,

±

+ 2 ±

2

− fk (1 − fk) mq + 2

2

.

× fk(1 − fk ) mq

1

1

1

1

Here fk is the electron distribution function, the sign + or − indicates the process of phonon emission or absorption, q, Ωq and mq are the phonon wave vector, frequency and occupation number, respectively. For equilibrium phonons the latter is described by the Planck function [exp ( Ωq /kB T )−1]−1. The matrix element of the indirect electron-photon interaction is presented in the form

(e vk )Vk±k(q)

Vk±k(q)(e

vk)

Rk k(q) =

·

Ωq

+

− ω

·

δk ±q ,k

Ek − Ek ±

Vk±k

=

e · (k − k) δk ±q ,k ,

(4.50)

m

ω

where Vk±k(q) is the matrix element of electron-phonon interaction, and the δ-symbol describes the in-plane momentum conservation in the scattering act. The first term in the right-hand side of (4.50) corresponds to the process of electron scattering by a phonon to the virtual state k followed by absorption of a photon while the second term describes the transition where the photon absorption precedes the scattering by a phonon.

The main features of the phonon-assisted intrasubband absorption can be understood neglecting interface e ects on the phonon energy spectrum and treating the electron-phonon interaction as that between 2D electrons and conventional 3D phonons. Then for the matrix element of electron interaction with polar-optical phonons in a zinc-blende QW structure one has

k k	± | |	V0(q2 + qz2)		æ∞ − æ0						1/2
V ± (q) =	i e		2π ΩLO	1			1			J(±)(qz ) ,	(4.51)
where	J(+)(qz ) = J(−) (qz ) =
							e−iqz z ϕe21(z) dz				(4.52)

and ϕe1(z) is the envelope function of a quantum-confined electron. In symmetrical QWs, J(+)(qz ) and J(−)(qz ) coincide and are real. A similar form has the matrix element for deformation-potential or piezoelectric interaction of

4.3 Intrasubband Optical Transitions

193

electrons with acoustic phonons. Particularly, for the deformation-potential interaction one has

									1/2
	Vk±k(q) =			q2		+ qz2
		i Ξc							J(±)(qz ) ,	(4.53)
						s
				0			LA

where Ξc is the deformation-potential constant, ρ is the density of the semiconductor and sLA is the longitudinal sound velocity.

In a symmetric QW with infinitely high barriers, the integral (4.52) equals

to

J(±)(qz ) = x		1 + π2 − x2 ,
	sin x		πx

where x = qz a/2. Values of [J(±)(qz )]2 are close to unity for x < π/2 and become negligible for x > 3π/2. Therefore, a typical value of qz in (4.53) is π/a while

	2	2m			¯
	q				max E, ω .
				2
This di ers from intraband optical transitions						in a bulk semiconductor where
2	2	2		is determined by max					¯
the square modulus qx + qy		+ qz							E, ω .
Figure 4.8 presents the calculated temperature							dependence of the absorp-

tion coe cient of GaAs/AlGaAs MQWs, K = η/d, at the wavelength λ = 92 µm ( ω = 13 meV) [4.11]. One can see the separate contributions to indirect absorption due to scattering by optical phonons, impurities and interface imperfections as well as a sum of these contributions.

Since the LO-phonon energy ΩLO in GaAs is 36 meV and ω < ΩLO, at low temperatures the light absorption of electrons interacting with LOphonons can be ignored and the scattering by static defects is dominating. With increasing temperature the role of transitions accompanied by LOphonon absorption increases. At the same time the step-like energy distribution of the degenerate 2D electron gas is smeared, and photon absorption followed by emission of a LO phonon also becomes possible. As a result, the optical-phonon assisted absorption is dominating starting with T = 200 K.

Agethe and Vass [4.12] have calculated the LO-phonon limited intrasubband photon absorption in n-doped QWs taking into account that the actual phonon spectrum is more complicated and consists of confined, interface (symmetric and antisymmetric), half-space and bulk modes. They analyzed the contribution to the absorption from each phonon mode as a function of four controllable parameters, namely, the light frequency ω, QW thickness a, electron temperature Te and density N2D.

4.3.2 Electron Cyclotron Resonance in a Superlattice

Cyclotron resonance is the most powerful technique for measuring the e ective masses in solids. In the classical description of the cyclotron resonance

194 4 Intraband Optical Spectroscopy of Nanostructures

)	4000		λ = 92 µm
-1
Κ (cm			T = 4.2 K
coefficient,	3000
						Sum
		Interface		Nonequilibrium
		roughness
	2000				phonons
Absorption
	1000	Impurity			Equilibrium
					phonons
	0	100		200	300	400

Electron temperature, Te (K)

Fig. 4.8. Calculated contributions of various scattering mechanisms to the farinfrared absorption coe cient of a biased n-doped GaAs/AlGaAs MQW structure for s-polarized light. In the calculation, interface scattering, impurity scattering, scattering by equilibrium and nonequilibrium phonons are taken into account. The sum of all contributions is shown by the solid line. From [4.11].

4.3 Intrasubband Optical Transitions

195

in the 3D space, the equation of motion (4.43) is replaced by the Lorentz equation

v˙ (t) + γv(t) =	e		v(t)		(4.54)
	m	E(t) +	c	× B ,

where B is an external static magnetic field and E(t) is an oscillating electric field. We assume E(t) B and use the system of coordinates with z B. Equation (4.54) is readily solved and the current-density combinations j± = jx ± ijy are given by

j±(ω) = eN3D v± =	e2N3D		E±(ω)		(4.55)
	m			,
			−i(ω ± ωc) + γ

where ωc the classical cyclotron frequency |e|Bz /(m c). When the frequency ω passes through the cyclotron frequency, either j+ (if Bz < 0) or j− (if Bz > 0) exhibits a resonant behavior and one observes the resonant absorption of electromagnetic radiation (microwave or far-infrared).

In quantum-mechanical terms, the cyclotron resonance originates from optical transitions of charged particles between the Landau levels. Measurement of the dependence of the cyclotron-resonance frequency on the magnitude and direction of the magnetic field provides a direct and reliable way for determining the electron or hole e ective mass, as well as for studying the nonparabolicity and nonsphericity of an electronic band in a semiconductor.

In a bulk semiconductor with a parabolic conduction band

Ek =	2	k2	k2	k2	,	(4.56)
	2	m1	+ m2	+ m3
		1	2	3

the Schr¨odinger equation for the envelope wave function in a homogeneous magnetic field can be simplified by change of the coordinates

		xi → x˜i =			m¯i		xi			(i = 1, 2, 3)
					m
to an equivalent equation for an						electron with the isotropic mass m¯ =
(m1m2m3)	1/3				˜
		in an e ective field B with the components
			B˜i =							Bi .	(4.57)
									m¯i
									m

Therefore, the energy spacing between the nearest Landau levels assumes the form

				˜		|e|B
	ωc	=	|e|B		=		,
			mc¯
						mcc
	where the cyclotron mass
	mc = m¯			m¯i	cos2 θi		−1/2
							,
		i		m

(4.58)

(4.59)

196	4 Intraband Optical Spectroscopy of Nanostructures
θi is the angle between B and the axis i.
	If two of the three masses mi coincide, for instance, if m1 = m2 ≡ mt,
the expression for the cyclotron mass simplifies to
	mc(θ3) =	sin2 θ3		cos2 θ3	−1/2
			+	mt2	,	(4.60)
		mtml
where ml ≡ m3. By measuring the cyclotron resonance in the B						3 and

B 3 geometries, one can determine the cyclotron masses mc(θ3 = 0) = mt
and mc(θ3 = π/2) =	√		and, hence, the longitudinal mass
		mtml
			m2(π/2)			(4.61)
			ml =	c
					.
				mc(0)

If B x3, the cyclotron orbit is a circle and has the scale of the magnetic length

	λB =	c	1/2
			.
		|e|B

If B x3, say, B lengths along x1

x2, the cyclotron orbit is elliptical with di erent magnetic and x3,

λB,x1

=

1/4

|e|B

1/2

, λB,x3

=

1/4

|e|B

1/2

mt

ml

. (4.62)

ml

c

mt

c

If the electron dispersion Ek has a more complex form than (4.56), one can use for determination of the cyclotron mass mc the semi-classical approach

mc(E, kz ) =	2		dkxdky δ(Ek − E) ,	(4.63)
	2π

where the z axis of the Cartesian coordinate system x, y, z is directed along the magnetic field. Of the states with a fixed electron energy E, the main contribution to the cyclotron resonance comes from those characterized by extremal orbits corresponding to a maximum or minimum of the kz -dependence of mc.

In QWs, the electron motion along the growth direction is quantized and the cyclotron orbits are confined to the interface plane. In terms of a 3D semiconductor it is equivalent to setting ml → ∞ in (4.60), which results in

a cosine dependence of the cyclotron mass
mc(θ) = m cos θ	(4.64)

on the angle θ between the normal to the interfaces and the magnetic field direction. This angular dependence, as a signature of the confinement of cyclotron orbits in MQWs with thick barriers, was first confirmed in the

4.3 Intrasubband Optical Transitions

197

˚

optically detected cyclotron resonance in a structure consisting of 180-A-

˚

thick GaAs wells separated by 230-A Al0.33Ga0.67As barriers [4.13]. These indirect methods for observing cyclotron and magnetic resonances, Optically Detected Cyclotron Resonance (ODCR) and Optically Detected Magnetic Resonance (ODMR), involve the monitoring of microwave-induced changes in the luminescence intensity.

In the case of SLs, coupling between wells through thin penetrable barriers transforms subbands of electron quantum-confined states into minibands of extended states. The energy dispersion of the latter has a 3D character. Therefore, the cyclotron resonance in SLs should reveal properties similar to those in a uniaxial semiconductor crystal with the longitudinal e ective mass drastically dependent on the barrier thickness. Particularly, the Landau levels are formed not only in the B z geometry as in the case of QWs but also in a magnetic field lying in the interface plane. According to (4.60), in the latter configuration the cyclotron mass is the geometric mean of the in-plane mass mt and the “superstructural” mass ml, and the spacing between Landau levels is smaller than in the former configuration. Landau levels in a SL were first observed in both configurations of the magnetic field by Belle et al. [4.14] who studied the photoluminescence excitation spectra of the structure con-

˚	˚
taining 40 periods of 39.2-A	GaAs wells and 11.2-A Al0.4Ga0.6As barriers.

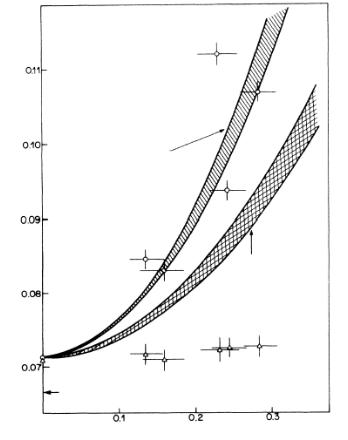
The first direct cyclotron-resonance measurements on extended states in a semiconductor SL were performed by Du eld et al. [4.15]. Figure 4.9 illustrates their measurements of the normal (ml) and in-plane (mt) e ective masses in a GaAs/AlxGa1−xAs as a function of the aluminum fraction x in the barriers. The curves bounding the shaded areas represent the ml(x) dependence calculated for a SL with rectangular wells and barriers, and for the conduction-band o set V = 0.65∆Eg or V = 0.61∆Eg using the KronigPenney boundary conditions

	ϕA = ϕB ,	dϕ	=	dϕ	(4.65)
		dz		dz
			A		B

or the Bastard boundary conditions (2.10).

The above picture of the cyclotron orbits in the geometry B x2 is valid at low magnetic fields when the magnetic length λB,z is larger than the SL period d, and an electron can complete its elliptical cyclotron orbit through several barriers. If the lattice periodicity and cyclotron orbit radius are comparable the electron energy gets dependent on the position of the cyclotron orbit along the growth axis z and one needs to solve explicitly the Schr¨odinger equation for the electron envelope function ψ(r) in a SL [4.16]. With B y and using the Landau gauge, Ax = Bz, Ay = Az = 0, this function can be sought in the form

ψ(r) = ei(kx x+ky y)ϕ(z) ,

(4.66)

where ϕ(z) satisfies the equation

198 4 Intraband Optical Spectroscopy of Nanostructures

Bastard

Mass

Kronig-Penney

Aluminum fraction in barrier

Fig. 4.9. E ective electron mass related to the free electron mass in the lowest

˚ ≈ ˚

miniband e1 in GaAs/AlxGa1−xAs SL with a = 80 A, b 20 A vs. composition x. The experimental data were obtained from a cyclotron resonance study. Circles, the normal mass ml ≡ mzz ; triangles, the in-plane mass mt ≡ mxx = myy . The calculations performed for the boundary conditions (4.65) and (2.10) are displayed by shaded areas. The curves bounding these areas correspond to the conductionband o set V = 0.65∆Eg (top curve) and V = 0.61∆Eg (bottom curve). From [4.15].

2

kx −

eB

2

ϕ(z) −

d 2 d

z

+ ky2

ϕ(z) + V (z)ϕ(z) = Eϕ(z) .

2m

c

dz

2m

dz

Here the notations x, y, z are used instead of x1, x2, x3, V (z) is the superstructure potential, and the e ective mass m is allowed to be di erent in the well and barrier materials. The position of the cyclotron orbit z0 = kxλ2B is a good quantum number. In the limit λB,z = (mt/ml)1/4λB d, the Landau levels are flat, i.e., they have the same energy for all values of z0. At

4.4 Infrared Reflection from Quantum Wells and Superlattices

199

higher fields, as the cyclotron energy approaches the miniband width, λB,z and d become comparable and the interlevel energy spacing as a function of B tends to saturate. Simultaneously, the Landau levels develop dispersion, and the resonant absorption spectrum broadens [4.17].

4.4 Infrared Reflection from Quantum Wells and Superlattices

Optical phonon modes dominate the infrared absorption and spectroscopic ellipsometry in undoped bulk semiconductors and multi-layered heterostructures. Infrared reflectance can be used as a simple, contactless and nondestructive, characterization technique to provide the information on the thicknesses of the various layers, alloy composition, phonon frequencies and broadening parameters. We consider here the infrared reflection spectroscopy from an undoped SL and its description in the e ective-medium dielectric function model.

For a crystal of cubic symmetry with two di erent atoms in the unit cell, the dielectric function in the infrared region can be represented in the form

	æ(ω) = æ	ΩL2	− ω2	− 2iΓLω	,	(4.67)
		∞ ΩT2 − ω2 − 2iΓT ω

where ΩL and ΩT are the resonance frequencies of the LO and TO phonon, respectively, æ∞ is the high-frequency dielectric constant, and ΓL, ΓT are the phonon damping rates. In general, ΓL = ΓT but usually these constants are assumed to coincide.

Let a SL consist of alternating layers of semiconductors A and B with the isotropic dielectric functions æA(ω) and æB(ω), described by (4.67) with a given set of parameters æ∞A , ΩT 1, ΩL1 for the layer A, and æ∞B , ΩT 2, ΩL2 for the layer B. For simplicity, in the main part of this section, we neglect the phonon damping. For an arbitrary relation between the light wavelength and the SL period d = a+b, one needs to use the straightforward treatment of the normal light waves in a periodic medium presented in Chap. 2. If the light wavelength is large compared to the SL period d = a + b, then, according to (2.132), the SL may be treated as a homogeneous uniaxial medium with two linearly independent components of the dielectric tensor,

æ (ω) ≡ æxx = æyy =		æA(ω)a + æB(ω)b		,	(4.68)
		a + b
æ (ω) ≡ æzz =	(a + b)æA(ω)æB(ω)
			.
	æA(ω)b + æB(ω)a

The function æ (ω) has poles at the points ω = ωT 1, ωT 2 and the function æ (ω) has zeros at the points ω = ωL1, ωL2. Denoting the zeroes of the function

æ (ω) .

200 4 Intraband Optical Spectroscopy of Nanostructures

æA(ω)a + æB(ω)b

by ω ,1, ω ,2 and those of the function

æA(ω)b + æB(ω)a

by ω ,1, ω ,2 we can represent the frequency dependence of the components

(4.68)	in a factorized form
	æ	(ω) = æ∞			(ω2 ,1 − ω2)(ω2 ,2 − ω2)				,	(4.69)
				(ΩT2 1 − ω2)(ΩT2 2 − ω2)
	æ	(ω) = æ∞			(ΩL2 1 − ω2)(ΩL2 2 − ω2)				,
where				(ω2,1 − ω2)(ω2,2 − ω2)
			æ∞a + æ∞b					(a + b)æ∞æ∞
	æ∞ =						, æ∞ =			(4.70)
			A	B				A	B .
				a + b				æA∞b + æB∞a

Note that in a SL with layers of equal thicknesses, a = b, the frequencies ω ,j and ω ,j coincide.

In a uniaxial medium, solutions of the Maxwell equations split into ordinary and extraordinary waves. For the ordinary waves (s- or TE-polarization), the electric vector E is perpendicular to the plane containing the light wave vector q and the principal axis. The dispersion equation has the form

q2 =

ω 2

c

For the extraordinary waves (p- or TM-polarization), the vector E lies in the plane (q, z), and the dispersion equation is

q2 = ω 2 æ (ω)æ (ω) ,

cæ (ω) cos2 θ + æ (ω) sin2 θ

where θ is the angle between q and z. For the reflection coe cient from the boundary between the vacuum and semi-infinite SL, one obtains

Rµ = |rµ|2 , rµ = 1 − n¯µ ,

1 + n¯µ

where the index µ = s, p indicates the polarization of the incident wave,

æ

sin2 θ0

1/2

1

æ − sin2

θ0

1/2

n¯s =

−cos θ0

, n¯p =

,

(4.71)

cos θ0

æ æ

and θ0 is the external angle of incidence.

If a SL is finite and grown on a substrate with an isotropic dielectric constant æb, one has to take into account the light reflection at the boundary