Климанов Сборник задач по теории переноса, дозиметрии и засчите 2011

		′		′ 2	]cos ψ;
	ω3 = ω3μs − k[1−(ω3 )
	ω2	=ω′2μs	+ k(ω′2ω′3 cos ψ+ ω1′ sinψ);			(1.44)
	ω1 =ω1′μs +k(ω1′ω′ 3 cosψ+ω′2 sinψ),
где k =	2		′ 2	].
	(1−μs	) /[1−(ω3 )

В случаях, когда |ω'3| ≈ 1, для определения направляющих косинусов рекомендуется использовать следующие выражения:

ω3 =ω′3μs ; ω2 =sinψ 1-μs2 ; ω1 =cosψ 1-μs2 .

(1.45)

6. Основные оценки функционалов в методе Монте-Карло. Пусть α = (x1, ..., xk ) – случайная траектория, начинающаяся в точ-

ке x1 и заканчивающаяся в точке xk, тогда для расчета функционалов поля излучения применяются следующие формулы:

а) оценка по поглощениям:

ξ(α) =	q1 (x1 )		W (x , x ) ...W (x		, x )	g(xk )		,	(1.46)
	P	(x )	1 2	k −1	k	P(x	)
1		1				k
где
K(x, y) / P(x, y),			если P(x, y) > 0;
W =
0, если P(x, y) = 0;

q1(x), K(x,y) – плотность первых столкновений и ядро переноса частиц в исследуемой среде; P1(x), P(x,y), P(x) – вероятности первых столкновений, перехода от столкновения в точке x к столкновению в точке y и поглощения в точке x соответственно; g(x) – функция отклика детектора для рассматриваемого функционала от плотности столкновений частиц;

б) оценка по столкновениям:

k

η(α) = ∑Wm (α)g(xm ),

(1.47)

m=1

где W

m

=

q1

(x1 )

W (x , x

2

) ...W (x

m−1

, x

m

);

P1

(x1 )

1

в) оценка по пробегу:

k

β(α) = ∑Wm dm g1m ;

(1.48)

m=1

где dm – длина m-пробега частицы в области V; g1m – функция отклика детектора для плотности потока на m-пробеге в области V;

г) локальная оценка (в точке x*)

41

	k	Wm (α)
	η1 (α) = ∑		K(xm , x )	(1.49)
	m=1	Σs (x )

Задачи

4.1. Случайная величина ξ имеет плотность распределения

f (x) = a / a2 − x2 , если| x |< a;

0, если| x |≥ a.

Определить коэффициент a, вероятность попадания ξ в интервал [a/2, a] и построить функцию распределения ξ.

4.2.Показать, что функция f(x) = 1/(x2 + π2) является плотностью распределения случайной величины ξ, и вычислить вероятность попадания случайной величины ξ в интервал (π, ∞).

4.3.Случайная величина характеризуется рядом распределения

xi	0	1	2	3	4
Pi	0,2	0,4	0,3	0,08	0,02

Определить математическое ожидание и дисперсию.

4.4.Вычислить дисперсию и среднеквадратическое отклонение для случайной величины ξ с равномерным распределением на отрезке [a, b].

4.5.Показать, что вероятность попадания на интервал [a, b] нормально распределенной случайной величины с математическим ожиданием m и среднеквадратическим отклонением σ не изменится, если каждое из чисел a, b, m и σ увеличить в λ раз.

4.6.Двухмерная случайная величина Q = {ξ, η} имеет плотность распределения

	≤ x ≤	π	; 0	≤ y ≤	π	;
asin(x + y), вобласти0		2			2
fQ (x, y) =
0, внеобласти.

Определить константу a; математические ожидания mξ, mη; среднеквадратические отклонения σξ, ση и коэффициенты корреляции

rξ,η.

4.7. В результате испытаний случайная величина ξ приняла сле-

дующие значения:
x1 = 2	x2 = 5	x3 = 7	x4 = 1	x5 = 10
x6 = 5	x7 = 9	x8 = 6	x9 = 8	x10 = 6

42

x11 = 2	x12 = 3	x13 = 7	x14 = 6	x15 = 8
x16 = 3	x17 = 8	x18 = 10 x19 = 6		x20 = 7
x21 = 3	x22 = 9	x23 = 4 x24 = 5		x25 = 6

Получить и построить график функции распределения F(x). 4.8. В результате испытаний значения равномерно распределен-

ной на отрезке [a, b] случайной величины ξ попали в заданные интервалы ( ) следующее число раз (n):

	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60
n	11	14	15	10	14	16

Определить значения a, b и плотность распределения f(x).

4.9.Случайная величина ξ имеет нормальное распределение

(0,1). Найти плотность распределения случайной величины η, если:

а) η = ξ2; б) η = exp(ξ).

4.10.Случайная величина ξ имеет показательное распределение. Найти плотность распределения η = 1/(1 – ξ).

4.11.Получить интегральное уравнение переноса для плотности

столкновений ψ(r , E,Ω) , где значения переменных фиксируются

перед столкновением, исходя из интегрального уравнения для дифференциальной плотности потока нейтронов (или фотонов)

ϕ(r, E,Ω) .

4.12. Выразить плотность столкновений χ(r, E,Ω) , где значения переменных фиксируются после столкновения, через функцию источника q(r, E,Ω) и дифференциальную плотность потока

ϕ(r, E,Ω) .

4.13. Получить интегральное уравнение переноса для плотности столкновений χ(r, E,Ω) исходя из интегрального уравнения для дифференциальной плотности потока нейтронов (или фотонов)

ϕ(r, E,Ω) .

4.14.Написать выражение для плотности первых выходящих столкновений для точечного изотропного моноэнергетического источника, считая, что на границе внешний поток отсутствует.

4.15.Найти первый компонент разложения в ряд Неймана цен-

ности входящих столкновений ψ1* (r , E,Ω) для детектора, регистрирующего в точке r0 интегральную плотность потока частиц, счи-

43

тая, что имеет место комптоновское рассеяние и эффект образования пар.

4.16. Преобразовать полученные в задачах (4.11) и (4.13) интегральные уравнения для плотности столкновений ψ(r, E,Ω) и χ(r, E,Ω) , выделив в явном виде ядро переноса

					r − r′
		δ		Ω −
					| r − r′
T (r′,r; E,Ω) = Σ(r, E) exp[− ∫ Σ(r′′, E) ds]						|
					′ 2
	r′→r			(r − r )
и ядро столкновений
′ ′	Σs (r, E′ → E,Ω′ → Ω)		.
C(E ,Ω ; E,Ω,r ) =	′
	Σ(r, E )

4.17.Частицы падают на плоский однородный слой вещества толщиной H. Движение частиц в веществе начинается из точки

x= 0 и происходит вдоль оси x с постоянным сечением взаимодей-

ствия. При столкновениях частицы с вероятностью 1- ps поглощаются, а с вероятностью ps –рассеиваются, но при этом не меняют направление движения вдоль оси x (односкоростная модель с дель- та-рассеянием).

Записать интегральное уравнение для плотности столкновений ψ(x) таких частиц и получить его решение.

4.18.Для условий задачи (4.17) записать сопряженное уравнение так, чтобы его решение ψ*(x) представляло вероятность того, что частица вылетела из слоя, испытав хотя бы одно столкновение. Получить решение этого уравнения.

4.19.Вывести явную формулу для определения значения, принимаемого случайной величиной ξ c плотностью распределения

f (x) = a exp[−a(x − x0 )] для x0 < x < ∞.

4.20. Доказать, что случайную величину ξ, определенную в интервале 0 < x < l с плотностью

f (x) = a exp(−ax) /[1− exp(−al)],

можно моделировать с помощью любой из трех формул:

ξ = − 1a ln{1− γ[1−exp(−al)]};

44

ξ= − 1a ln[γ + (1− γ) exp(−al)];

ξ= − 1a ln γ, если ξ < l.

4.21.Вывести явную формулу для расчета значений, принимаемых случайной величиной ξ с функцией распределения

	F(x) =1−	1	exp(−x) + exp(−5x)], 0 < x < l.
		3

4.22. Вывести явную формулу для определения значений, принимаемых случайной величиной ξ с плотностью распределения

	f ( y) =	2	1− y2 , −1 ≤ y ≤1.
		π

4.23. Написать явные формулы для определения значений, принимаемых случайной величиной ξ со следующей плотностью распределения:

а) f (x) ~ exp(−Σx), 0 ≤ x ≤ a, Σ > 0; б) f (x) ~ (x +1)2 , 0 ≤ x ≤1;

в) f (x) ~ |sin x|, − π/ 2 ≤ x ≤ π/ 2.

4.24.Написать алгоритм метода исключения для розыгрыша функции:

f(x) (3 - (2 x)1/3 ), 0 ≤ x ≤ 1.

4.25.Написать алгоритм метода исключения для розыгрыша функции:

f(x) x5/3( 1 - x )3/2 , 0 ≤ x ≤ 1.

4.26.Написать алгоритм метода исключения для получения значений случайной величины ξ со следущей плотностью распределения:

а) f(x) (3 − 3 2x, 0 ≤ x ≤1;

б) f(x) x5 / 3 (1− x)3/ 2 .

4.27. Разыграйте функцию

f(x) ( 1 + x )2, 0 ≤ x ≤ 1.

4.28. Сравните розыгрыш функции

f (x) = 4π(1+ x2 ) при 0 < x ≤1

методом обратной функции и методом исключения. 4.29. Сравните розыгрыш функции

45

f (x) = 2π 1− x2 при 0 < x ≤1

методом обратной функции и методом исключения.

4.30. Вывести явные формулы для определения координат случайной точки Q = (ξ,ζ), равномерно распределенной в плоском кольце:

R12 < x2 + y2 < R22 .

4.31. Вывести явные формулы для определения координат случайной точки Q = (ξ,ζ), определенной с плотностью f Q (x, y) = 3y в

треугольнике, ограниченном прямыми x = 0, y = x и y = 1.

4.32. Вывести явную формулу для определения значения, принимаемого случайной величиной ξ с плотностью распределения

f(x) = cos2 2πmx для 0 < x < 2, где m − целоечисло.

4.33.Случайная величина ξ имеет плотность распределения

f (x) = 2x, x (0,1). Рассчитать таблицу из четырех равновероятных

интервалов.

4.34. Плотность распределения случайной величины ξ имеет вид, показанный на рис. 1.9. Предложите алгоритм розыгрыша значений случайной величины, используя метод суперпозиции и метод обратных функций.

f(x)

fb

	fa
2	x

a b

Рис. 1.9. График плотности распределения случайной величины ξ

4.35. Предложите алгоритм вычисления интеграла

I = ∫1 exp(− x2 )dx

0

методом Монте-Карло с использованием выделения главной части. 4.36. Предложите алгоритм вычисления интеграла

46

I = ∫1 exp(− x2 )dx

0

методом Монте-Карло, используя метод существенной выборки. 4.37. Предложите алгоритм вычисления интеграла

I = ∫2 ln(x) dx

1

методом Монте-Карло и рассчитайте его дисперсию.

4.38.Источник излучения равномерно распределен по диску радиусом R. Вывести явные формулы для розыгрыша координат вылета частиц из диска (r,ψ).

4.39.Источник представляет собой сферу радиусом R с центром

вточке r0 , заполненную радиоактивной водой. Напишите алгоритм

розыгрыша декартовых координат точки рождения частицы.

4.40. Источник представляет собой цилиндр высотой H, радиусом основания R и осью, направленной вдоль оси z. Центр нижнего

основания находится в точке r0 . Цилиндр равномерно заполнен радионуклидным источником за исключением сферической полости радиуса ρ с центром в точке r1 находящейся внутри цилиндра. На-

пишите алгоритм розыгрыша декартовых координат точки рождения частицы.

4.41. Источник представляет собой усеченный конус с радиусами основания R1 и R2 и высотой H. Центр нижнего основания нахо-

дится в точке r0 . Он равномерно заполнен радиоактивной жидко-

стью. Напишите алгоритм розыгрыша декартовых координат точки рождения частицы.

4.42.Источник представляет два куба размерами a и b, соединенные между собой трубой длиной L и радиусом R. Источник равномерно и полностью заполнен раствором радиоактивного нуклида. Считая, что все геометрические параметры, определяющие взаимную конфигурацию емкостей заданы, предложите алгоритм розыгрыша точки рождения частицы.

4.43.Источник гамма-излучения представляет собой радионуклид 56Mn. Разыграйте случайное значение энергии вылетающей частицы, считая, что генератор случайных чисел выдал число 0,377.

4.44.Источник излучения представляет собой сферическую ячейку, ограниченную радиусами R1 и R2. Удельная мощность ис-

47

точника изменяется по закону S(r) = kr. Вывести явные формулы для розыгрыша координат вылета частицы в такой ячейке (r,θ,ψ).

4.45. Источник излучения представляет собой плоскость, излучающую в полупространство по закону: а) f (θ) cosθ; б)

f (θ) cosθ. Вывести явные формулы для розыгрыша координат

вылета частицы из источника (θ,ψ).

4.46. Источник излучения представляет собой плоскость, излучающую в полупространство. Угловое распределение изотропно по азимутальному углу ψ и представляет собой суперпозицию изотропного, cos θ, cos2 θ – распределений относительно полярного угла θ, измеряемого от нормали к плоскости источника. Относительный вклад каждого из распределений в суммарную мощность источника – p1, p2, p3 соответственно; p1 + p2 + p3 =1. Вывести яв-

ные формулы для определения координат вылета частицы из источника (θ,ψ).

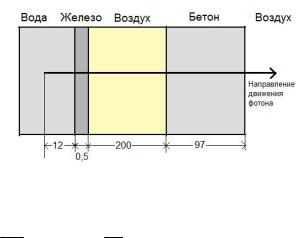
4.47. Для гамма-кванта с энергией 2 МэВ, вылетающего из столкновения в воде, определите случайный линейный (в см) пробег и вещество, в котором произойдет очередное столкновение. Луч из точки столкновения, направленный вдоль движения частицы, будет последовательно пересекать границы с железом через 12 см, с воздухом – еще через 0,5 см, с бетоном – еще через 200 см, а затем еще через 97 см – с бесконечной воздушной средой (рис.1.10). Принять, что число, полученное от генератора случайных чисел, равно

0,423.

Рис. 1.10. Геометрия задачи 4.47 (размеры указаны в см)

4.48. Дифференциальное сечение рассеяния представлено в виде: ddΩσ (Ω′ → Ω) = 4σπ1 +σ2 δ(Ω′−Ω).

Напишите алгоритм розыгрыша вылета частицы после рассеяния.

48

4.49.Предложите алгоритм розыгрыша угла отклонения фотона от первоначального направления движения при томсоновском рассеянии.

4.50.Рассчитать таблицу равновероятных интегралов для розы-

грыша косинуса полярного угла комптоновского рассеяния (μs) фотона с энергией E = 1 МэВ, взяв число равновероятных интервалов равным n =10.

4.51.Предложите алгоритм непосредственного моделирования косинуса и синуса азимутального угла при комптоновском рассеянии фотонов.

4.52.Фотон с энергией α = E/0,511 испытывает комптоновское рассеяние. Показать, что, во-первых, энергия фотона после рассеяния представляет собой случайную величину ξ с плотностью распределения f(x), пропорциональную функции

P(α, x) =

x

α

1

1

1

1

+

+

−

2

+

−

,

α

x

x

α

α

x

где x –энергия фотона после рассеяния в единицах mec2; во-вторых, значение энергии рассеянного фотона можно определить по следующему алгоритму:

	′			+ 2α+	1		′
			1
	ξ = ξ , если γ2						< P(α,ξ ),
					1+ 2α
′	α(1+2αγ1 )
где ξ =		.
	1+2α

В случае невыполнения условия выбирается новая пара случайных чисел

4.53.Показать, что для определения энергии фотона после ком-

птоновского рассеяния при начальной энергии E0 > 1,396 МэВ можно применить метод обратных функций в сочетании с методом суперпозиции.

4.54.Разыграть тип атома, на котором происходит взаимодействие, при столкновении фотона с энергией 0,2 МэВ с молекулой

глюкозы C6H12O6. Принять, что число, полученное от генератора случайных чисел, равно 0,719.

4.55.Разыграть вид взаимодействия на железе для фотона с энергией 0,15 МэВ. Принять, что случайное число, полученное от генератора, равно 0,261.

4.57.Определить новое направление движения фотона в сферических координатах, если перед рассеянием cos θ =0,5; cos ψ =

=sin ψ =0,707, а рассеяние произошло на μs =0,259 и cos ψ = sin ψ= =0,707.

49

4.58.Найти «вес» фотона после m рассеяний, если при моделировании его траектории вместо истинного углового распределения использовалось изотропное.

4.59.Полное сечение взаимодействия в среде равно

Σ(r, E) = Σs (r, E) + Σ(1)a (r , E) + Σ(a2) (r, E),

а при моделировании длины пробега частиц учитываются только сечения Σs (r , E) иΣ(1)a (r, E). Показать, что в этом случае каждой

частице следует после прохождения пути между столкновениями (L) приписать дополнительный «вес»

W (L) = exp[− ∫ Σ(2)a (r , E) dl],

(L)

4.60. Получить явные формулы для розыгрыша энергии и направления движения нейтрона после рассеяния на водороде, считая его изотропным в системе центра инерции.

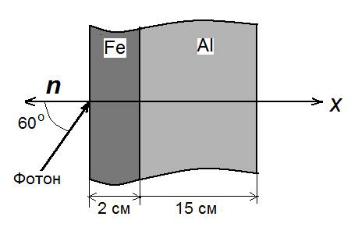
4.61. Фотоны с энергией E0 = 1,0 МэВ падают под углом θ0 = 60o к нормали на плоскую гетерогенную защитную сборку

(рис. 1.11). Пользуясь таблицей случайных чисел, определить с помощью аналогового моделирования следующие характеристики траекторий первых двух фотонов: а) координату z первого и второго взаимодействия; б) энергию рассеянных фотонов после первого и второго взаимодействий. Случайные числа, равномерно распределенные на отрезке [0, 1], приведены в табл. 1.4.

Рис. 1.11. Геометрия задачи 4.61

50