Медведева Основы теории множеств и теории отображений 2011

f : A ! B. Тогда для

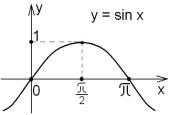
Поэтому f(x) 2 f(M1) или f(x) 2 f(M2). Следовательно, f(x) 2 2 f(M1) [ f(M2), то есть y 2 f(M1) [ f(M2).

Рассмотрим теперь элемент y такой, что y 2 f(M1) [ f(M2). Тогда y 2 f(M1) или y 2 f(M2). Если y 2 f(M1), то найдется элемент x1 2 M1, для которого f(x1) = y. Из условия x1 2 M1 следует, что x1 2 M1 [ M2. Поэтому f(x1) 2 f(M1 [ M2), то есть y 2 f(M1 [ M2). Если же y 2 f(M2), то найдется x2 2 M2, для которого f(x2) = y. Следовательно, x2 2 M1 [ M2, а потому f(x2) 2 f(M1 [ M2), то есть y 2 f(M1 [ M2).

Отсюда следует равенство f(M1 [ M2) = f(M1) [ f(M2).

Покажем, что образ пересечения двух множеств может не совпа-

дать с пересечением их образов.

Пример.

Рассмотрим

функцию

f

:

R

!

R

,

f(x) =

sin x.

Возь-

мем

M2

=

; ].

M1

=

[0; 2 ],

[ 2

Пересечением

этих

отрезков

явля-

ется

точка

2 . Поэтому образ

это-

го

пересечения

– точка

1, то

есть

f(M

1 \

M

) =

f

1

g. При этом

f(M

) =

2

1

= f([0;

2

]) = [0; 1], f(M2) = f([

2 ; ]) =

= [0; 1], и потому f(M1) \ f(M2) = [0; 1].

Отсюда

следует, что

f(M1 \ M2)

6=

Рис. 2.2

6= f(M1) \ f(M2).

Теорема 2.4. Пусть задано отображение любого множества M B выполняется

f 1(BnM) = Anf 1(M)

(прообраз дополнения равен дополнению прообраза).

Доказательство. Если элемент x 2 f 1(BnM), то f(x) 2 BnM. Значит, f(x) 62M, и поэтому x 62f 1(M). Следовательно, x 2 Anf 1(M). Если же x 2 Anf 1(M), то x 62f 1(M). Тогда f(x) 62M, то есть

f(x) 2 BnM. Поэтому x 2 f 1(BnM).

Отсюда следует, что f 1(BnM) = Anf 1(M).

Заметим, что образ дополнения, вообще говоря, не совпадает с дополнением образа.

Пример. Для функции f : [ 2; 2] ! [0; 4], f(x) = x2, и множества

M = [0; 2] имеем f([ 2; 2]nM) = f([ 2; 0)) = (0; 4], [0; 4]nf(M) = = [0; 4]nf([0; 2]) = [0; 4]n[0; 4] = ;, то есть f([ 2; 2]nM) 6= [0; 4]nf(M).

11

Дадим еще несколько определений.

Определение 2.2. Отображение f : A ! B для которого выполняется f(A) = B называется сюръекцией.

Для сюръекции говорят, что f является отображением множества A на множество B, поскольку для каждого y 2 B имеется x 2 A такой, что y = f(x).

Пример. Отображение f : R ! R, f(x) = x2, не является сюръекцией, так как f(R) = [0; +1) 6= R. Но функция f : R ! [0; +1), f(x) = x2, является сюръекцией.

Определение 2.3. Отображение f : A ! B называется инъекцией, если для любых двух различных элементов x1 и x2 множества A их образы f(x1) и f(x2) также различны.

Рис. 2.3

Пример. Функция f : R ! R, f(x) = x3, инъекция. А для функции f : R ! [0; +1), f(x) = x2, образы f( 2) = f(2), то есть эта функция не является инъекцией.

Определение 2.4. Если отображение f : A ! B является сюръекцией и инъекцией, то оно называется взаимно однозначным соответствием (биекцией) между множеством A и множеством B.

Из определения следует, что если функция f : A ! B является биекцией, то прообраз каждого элемента y 2 B состоит ровно из одного элемента множества A. На основании этого свойства определяется понятие обратной функции.

Определение 2.5. Пусть отображение f : A ! B является биекцией. Тогда на множестве B определено отображение, которое каждому элементу y 2 B ставит в соответствие тот элемент x 2 A для которого f(x) = y. Это отображение обозначается f 1 : B ! A и называется обратным для отображения f (обратная функция). Пишут x = f 1(y).

Обратим внимание на то, что ранее символ f 1 использовался для обозначения прообразов. В случае, если f является взаимно однозначным соответствием между A и B, запись x = f 1(y) означает и прообраз элемента y при отображении f и образ элемента y при отображении f 1.

12

Отметим также, что если f 1 – обратная функция для f, то, очевидно, функция f является обратной для функции f 1. Поэтому эти две функции называются взаимно обратными.

Определение 2.6. Пусть заданы два отображения f : A ! B и g : B ! C. Каждому x 2 A поставим в соответствие элемент g(f(x)) множества C. Таким образом определено отображение, которое обозначается g f : A ! C и называется сложным отображением (сложной функцией).

Рис. 2.4

Таким образом, (g f)(x) = g(f(x)). Часто еще используют названия "композиция отображений (функций)" и "суперпозиция отоб-

ражений (функций)".
Пример. Для отображения f : R !2		[ 1; 1], f(x) = sin x, и отобра-
жения g : [ 21; 1] !2	[0; 1], g(x) = 1 x , имеем (g f)(x) = g(f(x)) =
= 1 (sin x) = cos	x, g f : R ! [0; 1].

Заметим, что если f : A ! B и f 1 : B ! A – взаимно обратные функции, то для всякого x 2 A и y 2 B из определения сложной функции следует, что (f 1 f)(x) = x и (f f 1)(y) = y.

ГЛАВА 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА

Определение 3.1. Пусть задано множество M и каждой паре (x; y) элементов множества M сопоставлено действительное, неотрицательное число (x; y) так, что выполняются следующие три аксиомы: для любых элементов x, y, z множества M

1)(x; y) = 0 тогда и только тогда, когда x = y,

2)(x; y) = (y; x) (симметрия),

3)(x; z) (x; y) + (y; z) (неравенство треугольника). Функция называется метрикой, а число (x; y) – расстоянием

между элементами x и y множества M. Множество M с введенной метрикой называется метрическим пространством.

13

(; ) =

Легко проверить, что все аксиомы метриче-

Иначе говоря, метрика это функция : M M ! [0; +1), удовлетворяющая указанным трем аксиомам.

Обозначается метрическое пространство обычно так: (M; ) или просто M, если ясно, о какой метрике идет речь.

Для одного и того же множества M можно ввести различные метрики.

Пример. Для множества R всех действительных чисел можно определить метрику (; ) = j j, а можно определить другую метрику

1; 6= ;

0; = :

ского пространства в обоих случаях выполняются. Часто, говоря о метрическом пространстве R без указания метрики, подразумевают именно (; ) = j j.

Пример. Множество Rn всех упорядоченных наборов из n действительных чисел ( 1; :::; n) с расстоянием

p

(; ) = ( 1 1)2 + ::: + ( n n)2 ;

где = ( 1; :::; n), = ( 1; :::; n), является метрическим пространством.

Действительно, (; ) 0 для всех = ( 1; :::; n), = ( 1; :::; n) из Rn. Расстояние (; ) = 0 тогда и только тогда, когда 1 = 1, ...,n = n, то есть = .

Очевидно (; ) = (; ).

Докажем теперь,что (; ) (; ) + (; ) для всех ; ; из Rn. Имеем

nn

X	X
2(; ) =	( k k)2 = ( k k + k k)2 =
k=1	k=1

n

X

=( ( k k)2 + 2( k k)( k k) + ( k k)2 )

k=1

n

X

( ( k k)2 + 2j k kj j k kj + ( k k)2 ) =

k=1
n	n	n
X	X	X
=	( k k)2 + 2	j k kj j k kj + ( k k)2
k=1	k=1	k=1

14

n	v	n	v	n	n		=
k=1 ( k k)2 + 2uk=1 j k kj2			uk=1 j k kj2		+ k=1 ( k k)2
X	uX		uX		X
2	t		t2		2	:
=	( ; ) + 2 ( ; ) ( ; ) + ( ; ) = ( ( ; ) + ( ; ))

(Здесь мы использовали неравенство Коши–Буняковского для веще-

Следовательно, ( ; ) ( ; )	p				p
			.			b12 + :::bn2 .)
ственных чисел : a1b1 + ::: + anbn		a12	+ ::: + an2

+ ( ; )

Все аксиомы метрического пространства выполняются.

Пример. Возьмем множество Rn из предыдущего примера. Для этого множества можно определить другую метрику:

( ; ) = j 1 1j + ::: + j n nj

( здесь легко проверить справедливость аксиом метрического пространства).

Пример. Пусть M0 множество всех функций f : [0; 1] ! [0; 1]. Для функций f и g этого множества M0 обозначим

(f; g) = sup jf(x) g(x)j:

x2[0;1]

Тогда (f; g) 0. При этом (f; g) = 0 тогда и только тогда, когда f(x) = g(x) при всех x 2 [0; 1], то есть f = g.

Ясно, что (f; g) = (g; f).

Поскольку jf(x) h(x)j = jf(x) g(x)+g(x) h(x)j jf(x) g(x)j+

+jg(x) h(x)j при всех x 2		[0; 1], то (f; h) = sup jf(x) h(x)j
sup	jf(x) g(x)j + sup	x2[0;1]
		jg(x) h(x)j = (f; g) + (g; h).
x2[0;1]	x2[0;1]

Итак, выполняются все аксиомы из определения 3.1. Поэтому M0 – метрическое пространство с метрикой (f; g) = sup jf(x) g(x)j.

x2[0;1]

Пусть (M; ) – метрическое пространство и D – некоторое подмножество в M, то есть D M. Тогда D с тем же расстоянием (x; y), определенным теперь для пар элементов множества D, также является метрическим пространством. Тогда (D; ) называется подпространством пространства (M; ).

Часто элементы x метрического пространства называют точками независимо от свойств этих элементов. В метрическом пространстве M0 из последнего примера каждая функция f : [0; 1] ! [0; 1] является точкой пространства M0.

15

Введем основные понятия теории метрических пространств.

Определение 3.2. Открытым шаром O(x0; r) с центром в точке x0 и радиусом r в метрическом пространстве (M; ) называется совокупность всех точек x 2 M таких, что (x; x0) < r.

Открытый шар радиуса ", " > 0, с центром x0 называется также "-окрестностью точки x0 и обозначается O"(x0).

В пространстве R с метрикой ( ; ) = j j

окрестность O"(x0) –

это интервал (x0 "; x0 + ").

окрестность O"(x0; y0) – круг f(x; y)2R2

: (x px0)2

+ (y y0)2

< "2g.

В пространстве

R2

с метрикой ( ; ) =

( 1

1)2

+ ( 2

2)2

f

2p

g

В R

3

с метрикой ( ; ) =

3( 1 1)

2

2+ ( 2

)2 + (

3

)2

:2

O"(x0; y0; z0) – шар

(x; y; z)

R

: (x

x0)

+(y

y0)

+(z

z0)

< " .

Определение 3.3. Замкнутым шаром Z(x0; r) с центром в точке x0 и радиусом r в метрическом пространстве (M; ) называется совокупность всех точек x 2 M таких, что (x; x0) r.

Определение 3.4. Множество A M называется открытым в пространстве (M; ), если для каждого x 2 M существует "-окрест- ность O"(x) M.

В частности, всякий открытый шар O(x0; r) – открытое множество (и этим объясняется такое название шара).

Пустое множество ; и все множество M являются открытыми в пространстве (M; ).

Открытые множества обладают следующими свойствами.

Теорема 3.1. 1. Объединение любого числа (конечного или бесконечного) открытых множеств является открытым множеством.

2. Пересечение любого конечного числа открытых множеств является открытым множеством.

Доказательство

1. Пусть задано семейство множеств A , 2 , где все множества

A являются открытыми. Рассмотрим произвольную точку x 2									A .
					x		A		2		–
Тогда существует		из множества		такое, что		2		.	S

открытое множество, то существует " > 0 для которого "-окрестность

O"(x) A . Следовательно, O"(x)					A . Получили, что множе-
					2
ство		A	вместе со своей точкой x Sсодержит и некоторую ее "-
	2
окрестность.S			Значит,	A – открытое множество.
			2
2.	Пусть		A1, A2,S	..., An – открытые множества, а точка
x 2 A1		T::: TAn. Тогда точка x принадлежит каждому из множеств

16

A1, ... , An. Так как они все открыты, то существуют "1 > 0, ..., "n > 0

такие, что O"1 (x) A1, ..., O"n (x) An. Возьмем " = minf"1; :::; "ng. Для этого " и каждого номера k, 1 k n, имеем O"(x) O"k (x),

T T

а значит, O"(x) Ak. Поэтому O"(x) A1 ::: An. Следовательно,

TT

множество A1 ::: An является открытым.

Определение 3.5. Пусть множество A M. Точка x 2 M называется изолированной точкой множества A, если существует " > 0 такое, что окрестность O"(x) не содержит точек из M, отличных от точки x.

Определение 3.6. Пусть множество A M. Точка x называется предельной точкой множества A, если для любого " > 0 окрестность O"(x) содержит бесконечно много точек из M.

Предельная точка может принадлежать множеству A и может не принадлежать A.

Определение 3.7. Пусть A M. Замыканием множества A называется объединение множества A и всех его предельных точек и обозначается A.

Теорема 3.2. Операция замыкания обладает свойствами:

1)множество A состоит из всех точек x таких, что любая "-окрестность точки x содержит хотя бы одну точку из A;

2)A A;

3)(A) = A;

4)если A1 A2, то A1 A2;

5)A1 [ A2 = A1 [ A2.

Доказательство. Свойства 1, 2 следуют непосредственно из определения.

3. Пусть x 2 (A). Рассмотрим произвольное " > 0. Тогда по свойству 1 получим, что существует точка y 2 O"(x) такая, что y 2 A. Обозначим число "0 = " (x; y). Снова по свойству 1 получим, что существует точка z 2 O"0 (y) такая, что z 2 A. Тогда (z; x)

(z; y) + (y; x) < "0 + (y; x) = " (x; y) + (y; x) = ". Получили, что во всякой "-окрестности точки x найдется точка множества A,

что по свойству 1 означает x 2 A. Итак, (A) A. По свойству 2 имеем

A (A). Значит, (A) = A.

4.Это свойство следует из того, что предельные точки множества A1 являются заодно и предельными точками множества A2.

5.Имеем A1 A1 [ A2 и A2 A1 [ A2. По свойству 2 отсюда следует, что A1 A1 [ A2 и A2 A1 [ A2. Поэтому A1 [A2 A1 [ A2.

17

Рассмотрим теперь точку x 2 A1 [ A2. Докажем, что тогда x 2 A1 [ A2. От противного. Предположим, что x 62A1 [ A2. Отсюда

получим x 62A1 и x 62A2. Значит, существует "1 > 0, для которого окрестность O"1 (x) не содержит точек множества A1, и существует "2 > 0, для которого O"2 (x) не содержит точек из A2. Обозначим через " наименьшее из чисел "1 и "2. Тогда O"(x) не содержит точек из A1 и не содержит точек из A2. Поэтому O"(x) не содержит точек из A1 [A2.

Следовательно, x 62A1 [ A2. Противоречие. Значит, A1 [ A2 A1[A2.

Таким образом, A1 [ A2 = A1 [ A2.

Определение 3.8. Множество A M называется замкнутым, если A = A, то есть A содержит все свои предельные точки.

Из предыдущей теоремы следует, что замыкание A любого множества A – замкнутое множество.

Пустое множество ; и все множество M являются замкнутыми в пространстве (M; ).

Заметим, что эти два множества ; и M одновременно и открытые и замкнутые в метрическом пространстве (M; ).

Теорема 3.3. Множество A замкнутое тогда и только тогда, когда его дополнение MnA до всего множества M является открытым.

Доказательство. Если A замкнуто, то A = A, и, значит, A состоит из всех точек x таких, что любая "-окрестность точки x содержит хотя бы одну точку из A. Поэтому для каждой точки x 62A, то есть x 2 MnA, найдется " > 0 такое, что O"(x) не содержит точек множества A. Это означает O"(x) MnA. Следовательно, по определению, множество MnA открыто.

Пусть теперь MnA открыто. Тогда для каждой точки x 2 MnA, найдется " > 0 такое, что O"(x) MnA. Значит, O"(x) не содержит точек множества A. Поэтому все точки x 2 MnA не являются предельными для множества A. Следовательно, множество A содержит все свои предельные точки, что означает замкнутость A.

Поскольку Mn(MnA) = A, то есть дополнением множества MnA до всего множества M является множество A, эту теорему можно сформулировать по-другому:

Теорема 3.4. Множество A открытое тогда и только тогда, когда его дополнение MnA до всего множества M является замкнутым.

С помощью принципа двойственности легко доказать следующие свойства замкнутых множеств.

18

Теорема 3.5. 1) Пересечение любого числа (конечного или бесконечного) замкнутых множеств является замкнутым множеством.

2) Объединение любого конечного числа замкнутых множеств является замкнутым множеством.

Доказательство. 1. Пусть задано семейство множеств A , 2 , где все множества A замкнуты. Тогда все множества MnA являются

открытыми и по теореме 3.1 их объединение								(MnA ) также откры-
				M			2
то. По принципу двойственности					n	A	S	(MnA ), и, значит,
T		A				2		2
дополнение множества	A до всегоTмножестваSM открыто. Следо-
2	T
вательно, само множество				замкнуто.

2

2. Пусть A1, A2, ..., An – замкнутые множества. Тогда множества MnA1, ..., MnAn являются открытыми. По теореме 3.1 их пересечение

	T		T
(MnA1)		:::	(MnAn) открыто. В силу принципа двойственности
Mn(A1	S	::: SAn) = (MnA1) T::: T(MnAn). Значит, дополнение мно-

SS

жества A1 ::: An до всего множества M является открытым. По-

SS

этому само множество A1 ::: An замкнуто.

Замечание. Замкнутый шар (см. определение 3.3) Z(x0; r) в метрическом пространстве (M; ) – замкнутое множество (этим и объясняется такое название шара).

Действительно, каждая точка x множества MnZ(x0; r) принадлежит этому множеству вместе со своей "-окрестностью, где " = "(x) =

(x;x0) r . Значит, множество MnZ(x0; r) открыто. В силу теоремы 3.3

2

множество Z(x0; r) замкнуто.

ГЛАВА 4. ПОСЛЕДОВАТЕЛЬНОСТИ. ОТОБРАЖЕНИЯ МЕТРИЧЕСКИХ ПРОСТРАНСТВ

Определим сначала понятие последовательности в метрическом пространстве. Пусть M – метрическое пространство и каждому n 2 N поставлен в соответствие элемент an метрического пространства M. Тогда говорят, что задана последовательность точек a1, a2, ..., an,...

в метрическом пространстве M.

Это определение означает, что задать последовательность точек метрического пространства – это задать некоторую функцию

19

f : N ! M.

Кратко последовательность обозначают fang1n=1 или fang.

Определение 4.1. Последовательность fang называется сходящейся, если существует точка a 2 M такая, что для всякого " > 0 найдется номер N = N(") 2 N такой, что при всех n N выполняется (an; a) < " (то есть an 2 O"(a)). При этом точка a называется пределом последовательности fang и последовательность fang

называется сходящейся к точке a. Пишут a = lim an.

n!1

Из этого определения следует, что a = lim an тогда и только тогда,

n!1

когда lim (an; a) = 0.

n!1

Последовательности метрического пространства, не являющиеся сходящимися, называются расходящимися.

Утверждение 4.1. Сходящаяся последовательность элементов метрического пространства имеет единственный предел.

Доказательство. От противного. Предположим, что lim an =a

n!1

	(a; b)
и nlim!1 an = b, причем a 6= b. Тогда (a; b) 6= 0. Обозначим " =		.
	2

Для этого " существует номер N1 такой, что при всех n N1 выполняется (an; a) < " и существует номер N2 такой, что при всех n N2 выполняется (an; b) < ". Возьмем N = max fN1; N2g. Тогда при всех n N выполняется (an; a) < " и (an; b) < ", а из неравенства треугольника следует, что

(a; b) (a; an) + (an; b) < " + " = (a; b) + (a; b) = (a; b):

2 2

Итак, получили (a; b) < (a; b). Противоречие.

Пусть заданы последовательность fang1n=1 элементов метрического пространства и возрастающая последовательность натуральных чисел k1, k2,..., kn,... . Тогда последовательность fbng1n=1, где bn = akn , n 2 N, называется подпоследовательностью последовательности fang1n=1. Записывают подпоследовательность ak1 , ak2 ,...,akn ,... . Крат-

ко fakn g1n=1 или fakn g.

Непосредственно из определений следует, что если последовательность fang1n=1 сходится к a, то и любая ее подпоследовательность сходится к a.

Теорема 4.1. Точка a является предельной точкой множества A тогда и только тогда, когда существует последовательность fang

20