Медведева Основы теории множеств и теории отображений 2011

полняется k=1(MnAk) = M. Тогда ; = MnM = Mn			(MnAk)!	=
	m		m
m	S	m	k[
			=1

\\

=(Mn(MnAk)) = Ak 6= ;. Противоречие. Следовательно, из

k=1

k=1

всякой последовательности точек пространства (M; ) можно выделить сходящуюся подпоследовательность.

В качестве следствия из этой теоремы получим следующую.

Теорема 6.4. Компактное метрическое пространство является полным.

Доказательство. Пусть (M; ) – компактное метрическое пространство. Возьмем произвольную фундаментальную последовательность его точек. Тогда из нее можно выбрать подпоследовательность, сходящуюся к некоторой точке из M. По утверждению 5.2 отсюда следует, что и сама фундаментальная последовательность сходится к этой же точке. Поскольку всякая фундаментальная последовательность сходится, то пространство (M; ) – полное.

Теорема 6.5. Если в метрическом пространстве из всякой последовательности его точек можно выделить сходящуюся подпоследовательность, то это пространство компактно.

Доказательство. Пусть (M; ) – данное метрическое пространство. Докажем, что для всякого множества A M и всякого " > 0 существует покрытие множества A, состоящее из конечного числа открытых шаров радиуса " с центрами из множества A. От противного. Предположим, что при некотором "0 > 0 любое конечное число открытых шаров радиуса "0 с центрами из A не образует покрытия множества A. Возьмем в A произвольную точку x1. Один шар O"0 (x1) не образует покрытия множества A. Поэтому существует точка

x2 2 (AnO"0 (x1)). Для этой точки (x2; x1) "0 (так как x2 62O"0 (x1)). Два шара O"0 (x1) и O"0 (x2) также не образуют покрытия множества

	2
A. Поэтому существует точка x3 2 (An	kS
	O"0 (xk)). Для x3 имеем
	=1

(x3; x1) "0, (x3; x2) "0 (так как x3 62O"0 (x1) и x3 62O"0 (x2)). И так далее. Если точки x1, ..., xn уже выбраны, то точку xn+1 выбираем

n

S

из непустого множества An O"0 (xk). Тогда для нее все расстояния

k=1

(xn+1; xi) "0, i = 1; :::; n. Таким образом, получим последовательность x1; x2; ::: точек множества M из которой нельзя выбрать сходящуюся подпоследовательность, поскольку при всех n 2 N, m 2 N,

31

2n 1

1

2n 1

1

2k 1

1

n 6= m, выполняется неравенство (xn; xm) "0. Противоречие. Пусть семейство открытых множеств fG g – покрытие M. Пред-

положим, что из него нельзя выбрать конечное подпокрытие множества M. Возьмем покрытие множества M, состоящее из конечного числа открытых шаров радиуса 1. Тогда семейство fG g является покрытием каждого из этих шаров. Значит, для одного из этих шаров O1(x1) (с центром в некоторой точке x1 2 M), из покрытия fG g нельзя выбрать конечное подпокрытие. Возьмем теперь покрытие шара O1(x1) конечным числом открытых шаров радиуса 12 , центры которых принадлежат O1(x1). Тогда также найдется некоторый

шар O1 (x2), x2 2 O1(x1), для которого из покрытия fG g нельзя вы-

2

брать конечное подпокрытие. Затем шар O1							(x2) покрываем конечным
						2
числом шаров радиуса		1	с центрами из O1						(x2) и так далее. Полу-
		2
	2						2
чим шары O1(x1), O1 (x2), O				1	(x3), ..., O	1			(xn), ..., для каждого из
2	22					2n 1

которых из покрытия fG g нельзя выбрать конечное подпокрытие. Причем для всех k 2 N выполняется xk+1 2 O (xk) Следователь-

но, при всех n 2 N, m 2 N, m > n, имеем (xn; xm) (xn; xn+1)+

+ (xn+1; xn+2) + ::: + (xm 1; xm)	1	+	1	+ ::: +	1			2	.
	2n 1		2n		2m 2			2n 1

Значит, последовательность fxng фундаментальна. По условию из нее можно выделить подпоследовательность сходящуюся к некоторой точке x0 2 M. С помощью утверждения 5.2 получим, что тогда и сама последовательность fxng сходится к x0. Поскольку fG g – покрытие M, то точка x0 принадлежит некоторому множеству G 0 . Так как G 0 открыто, то при некотором > 0 окрестность O (x0) G 0 . Име-

ем x0	= lim xn и радиусы шаров O	1	(xn) стремятся к нулю при
	n!1	2n 1

n ! 1, а значит, найдется такой номер N, что при всех n N шары O (xn) O (x0) G 0 . Итак, начиная с номера N, все шары

O (xn) накрываются одним множеством G 0 . А мы брали эти шары

так, что на каждом из них из покрытия fG g нельзя выбрать конечное подпокрытие. Противоречие.

Следовательно, из всякого покрытия множества M можно выбрать конечное подпокрытие. Поэтому M – компакт.

Из теорем 6.3 и 6.5 следует теорема 6.6.

Теорема 6.6. Метрическое пространство компактно тогда и только тогда, когда из всякой последовательности его точек можно выделить сходящуюся подпоследовательность (к точке из этого пространства).

32

В качестве следствия из теоремы 6.6 получим теорему 6.7.

Теорема 6.7. Подмножество A M метрического пространства (M; ) компактно тогда и только тогда, когда из всякой последовательности точек множества A можно выделить подпоследовательность, сходящуюся к точке из A.

В главе 7 будет доказано необходимое и достаточное условие компактности множества A Rn.

Докажем теперь некоторые свойства отображений компактных метрических пространств.

Теорема 6.8. Образ компакта при непрерывном отображении метрических пространств – компакт.

Доказательство. Пусть (M1; 1) и (M2; 2) – метрические пространства, отображение f :M1 !M2 непрерывно, K – компакт, K M1. Рассмотрим произвольное покрытие множества f(K) открытыми множествами G . Поскольку при непрерывном отображении прообраз открытого множества открыт, то все множества f 1(G ) – открытые.

S	S
Из f(K) G следует K	f 1(G ). В силу компактности K

можно выбрать конечное подпокрытие f 1(G 1 ) [ ::: [ f 1(G m ) K. Тогда G 1 [ ::: [ G m f(K). Итак, всякое покрытие множества f(K) содержит конечное подпокрытие. Поэтому f(K) компакт.

Определение 6.3. Отображение f : M ! R называется ограниченным, если существует такое число " > 0, что при всех x 2 M справедливо jf(x)j ".

Теорема 6.9. Пусть M – компакт, отображение f : M ! R непрерывно. Тогда f ограничено и достигает своих точных верхней и нижней граней.

Доказательство. Из предыдущей теоремы следует, что f(M) компакт. Тогда по теореме 6.2 множество f(M) замкнуто.

Докажем ограниченность функции f. От противного. Предположим, что для всякого " > 0 найдется элемент x" 2 M такой, что jf(x")j > ". Элемент x1 2 M выберем произвольным образом и зафиксируем. Для " = jf(x1)j + 1 существует x2 2 M такой, что jf(x2)j > > jf(x1)j+ 1. Затем найдем x3 2 M для которого jf(x3)j > jf(x2)j+ 1 и т.д. Таким образом выберем элементы x1; x2; ::: множества M для которых jf(xn+1)j > jf(xn)j+ 1, n 2 N. Тогда при всех n 2 N, m 2 N, n 6= m имеем jf(xn) f(xm)j > 1. Поэтому из последовательности ff(xn)g1n=1 нельзя выбрать сходящуюся подпоследовательность, что противоречит компактности множества f(M). Следовательно, существует такое

33

число " > 0, что при всех x 2 M справедливо jf(x)j ".

Из теории действительных чисел известно, что всякое непустое замкнутое ограниченное подмножество из R содержит точные верхнюю и нижнюю грани. Отсюда следует утверждение этой теоремы.

ГЛАВА 7. НОРМИРОВАННЫЕ ПРОСТРАНСТВА

Определение 7.1. Непустое множество L называется вещественным линейным пространством, если выполняются следующие условия.

1.Для любых двух элементов x и y множества L однозначно определен третий элемент множества L, называемый их суммой и обозначаемый x + y, причем:

1) при всех x 2 L, y 2 L справедливо x + y = y + x (коммутативность);

2) при всех x 2 L, y 2 L, z 2 L справедливо (x + y) + z = x + (y + z) (ассоциативность);

3) существует такой элемент множества L, обозначаемый 0, что для всех x 2 L сумма x + 0 = x; элемент 0 называется нулевым

или нулем пространства L;

4) для всякого x 2 L существует такой элемент x0 2 L, что x + x0 = 0; элемент x0 называется противоположным к элементу x и обозначается x.

2.Для любого числа 2 R и любого x 2 L определен элемент множества L, называемый произведением на x и обозначаемый x, причем:

1) при всех 2 R, 2 R, x 2 L справедливо ( x) = ( )x,

2) при всех 2 R, 2 R, x 2 L справедливо ( + )x = x + x, 3) при всех 2 R, x 2 L, y 2 L справедливо (x + y) = x + y, 4) для всякого x 2 L выполняется 1 x = x.

Если в определении линейного пространства во втором пункте вместо произвольных вещественных чисел взять произвольные комплексные числа, то получим определение комплексного линейного пространства.

Если мы будем рассматривать вещественное линейное пространство, то запишем L(R), а если комплексное, то L(C). Всюду, где наши рассуждения верны и для вещественных и для комплексных линейных пространств, будем говорить просто о линейном пространстве и писать L.

34

Линейные пространства называют также векторными пространствами, а их элементы – векторами и вместо x иногда пишут ~x.

Вектор x + ( y) будем обозначать x y.

Докажем некоторые простые свойства линейных пространств.

Утверждение 7.1. Пусть L – линейное пространство. Тогда:

1)нулевой элемент пространства L единственный;

2)для всякого x 2 L противоположный ему элемент единствен-

ный;

3)для всякого x 2 L выполняется 0 x = 0;

4)для всякого x 2 L выполняется ( 1) x = x.

Доказательство. 1) Если 01 и 02 нули пространства L, то

01 = 01 + 02 = 02 + 01 = 02.

2)Пусть x 2 L и x1, x2 – элементы противоположные к x. Тогда x+x1 = 0 и x+x2 = 0. Отсюда x1 = x1+0 = x1+(x+x2) = (x1+x)+x2 =

=0 + x2 = x2.

3)Пусть x 2 L. Тогда 0 x = (0 + 0) x = 0 x + 0 x. Прибавим к

обеим частям последнего равенства элемент (0 x) противоположный к 0 x. Получим 0 x + ( 0 x) = (0 x + 0 x) + ( (0 x)). Поэтому 0 = 0 x + (0 x + ( 0 x)) = 0 x + 0 = 0 x.

4)Пусть x 2 L. Тогда x + ( 1) x = 1 x + ( 1) x = (1 + ( 1)) x =

=0 x = 0. Значит, ( 1) x = x.

Определение 7.2. 1) Элементы a1; :::; ak линейного пространства L(R) называются линейно зависимыми, если существуют такие вещественные числа 1; :::; k, не все равные нулю, что

1a1 + ::: + kak = 0.

2) Элементы a1; :::; ak линейного пространства L(R) называются линейно независимыми, если 1a1 + ::: + kak = 0 тогда и только тогда, когда 1 = 0; :::; k = 0.

Определение 7.3. 1) Элементы a1; :::; ak линейного пространства L(C) называются линейно зависимыми, если существуют такие комплексные числа 1; :::; k, не все равные нулю, что

1a1 + ::: + kak = 0.

2) Элементы a1; :::; ak линейного пространства L(C) называются линейно независимыми, если 1a1 + ::: + kak = 0 тогда и только тогда, когда 1 = 0; :::; k = 0.

Определение 7.4. Если в линейном пространстве L имеется n линейно независимых элементов, а любые n+1 элементов этого пространства линейно зависимы, то говорят, что пространство L имеет размерность n (L – n-мерное пространство). Если же в L мож-

35

но указать систему из любого конечного числа линейно независимых элементов, то говорят, что пространство L бесконечномерно.

Определение 7.5. Базисом n-мерного пространства L называется упорядоченная система из n линейно независимых элементов этого пространства.

Теорема 7.1. Пусть L = L(R) (L = L(C)) – n-мерное линейное пространство и e1; :::; en – его базис. Тогда всякий вектор x 2 L можно представить, причем единственным образом, в виде x = 1e1 + ::: + nen, где 1; :::; n – вещественные (комплексные) числа.

Доказательство. Пусть x 2 L. Поскольку L – n-мерное пространство, то n+1 векторов e1; :::; en; x линейно зависимы. Значит, найдутся

числа 1, ..., n, n+1, не все			равные		нулю, такие, что
1e1 + ::: + nen + n+1x	= 0. При этом n+1				6= 0, иначе векторы
e1; :::; en были бы линейно зависимы. Отсюда
x =	1	e1 + ::: +	n	en:
	n+1		n+1

Докажем теперь единственность представления. Пусть x 2 L и выполняются равенства x = 1e1 + ::: + nen, x = 1e1 + ::: + nen. Тогда

0 = x x = ( 1e1 + ::: + nen) ( 1e1 + ::: + nen) = ( 1 1)e1+ +::: + ( n n)en. В силу линейной независимости элементов e1; :::; en отсюда следует, что 1 1 = 0, ..., n n = 0, то есть 1 = 1, ...,n = n. Теорема доказана.

Представление произвольного вектора x n-мерного пространства в виде x = 1e1 +:::+ nen называется разложением вектора x по базису e1; :::; en. Числа 1; :::; n называются координатами вектора x в базисе e1; :::; en.

Определение 7.6. Функция f : L ! R, ставящая каждому элементу x линейного пространства L(R) (L(C)) в соответствие вещественное число jjxjj, называется нормой в линейном пространстве L (пишут f(x) = jjxjj), если удовлетворяет следующим аксиомам:

1)для любого x 2 L справедливо jjxjj 0; причем jjxjj = 0 тогда и только тогда, когда x = 0

2)для любых x 2 L, 2 R ( 2 C) справедливо jj xjj = j j jjxjj,

3)для любых x 2 L, y 2 L выполняется jjx + yjj jjxjj + jjyjj.

Линейное пространство L, в котором задана норма, называется линейным нормированным пространством.

36

Если L – линейное нормированное пространство с нормой jj:::jj, то, положив для произвольных элементов x 2 L, y 2 L расстояние(x; y) = jjx yjj, получим, что L – метрическое пространство с введенной метрикой . Действительно, для всех x 2 L, y 2 L, z 2 L:

(x; y) = jjx yjj 0;

(x; y) = jjx yjj = 0 тогда и только тогда, когда x y = 0, то есть x = y;

(x; y) = jjx yjj = jj( 1) (y x)jj = jjy xjj = (y; x);

(x; y) = jjx yjj = jj(x z) + (z y)jj jjx zjj + jjz yjj = = (x; z) + (z; y).

Итак, всякое линейное нормированное пространство с нормой jj:::jj является заодно и метрическим пространством с метрикой(x; y) = jjx yjj. Поэтому все понятия и утверждения, изложенные в этом пособии для метрических пространств, переносятся на нормированные пространства. В частности, всюду далее, если мы будем говорить о сходимости последовательности, пределе последовательности в нормированном пространстве L с нормой jj:::jj, непрерывности функции и т.д., то мы будем иметь ввиду соответствующие понятия для метрического пространства (L; ), где (x; y) = jjx yjj.

Повторим здесь некоторые определения из теории метрических пространств, используя понятие нормы.

Определение 7.7. Открытым шаром O(x0; r) с центром в точке x0 и радиусом r в линейном нормированном пространстве L называется совокупность всех точек x 2 L таких, что jjx x0jj < r.

Открытый шар радиуса ", " > 0, с центром x0 называется также "-окрестностью точки x0 и обозначается O"(x0).

Определение 7.8. Замкнутым шаром Z(x0; r) с центром в точке x0 и радиусом r в линейном нормированном пространстве L называется совокупность всех точек x 2 L таких, что jjx x0jj r.

Определение 7.9. Последовательность fang элементов линейного нормированного пространства L называется сходящейся, если существует точка a 2 L такая, что для всякого " > 0 найдется N = N(") 2 N такое, что при всех n N выполняется jjan ajj < " (то есть an 2 O"(a)). При этом точка a называется пределом последовательности fang и последовательность fang называется схо-

дящейся к a. Пишут a = lim an.

n!1

Из этого определения следует, что a = lim an тогда и только тогда,

n!1

когда lim jjan ajj = 0.

n!1

37

Теорема 7.2. Пусть L – линейное нормированное пространство, последовательности элементов этого пространства fxng и fyng сходятся, числовая последовательность f ng сходится, причем

lim xn = x,	lim yn = y,	lim n = . Тогда последовательности
n!1	n!1	n!1

fxn +yng и f nxng сходятся, и nlim (xn +yn) = x+y, nlim nxn = x.
!1			!1
Доказательство. 1) Возьмем произвольное " > 0. Тогда найдутся
						"
номера N1; N2 такие, что при всех n N1			выполняется jjxn xjj <
								2
"
и при всех n N2 выполняется jjyn yjj<		. Обозначим N =max fN1; N2g.
	2
При всех n N имеем			"			"
jj(xn+yn) (x+y)jj = jj(xn x)+(yn y)jj jjxn xjj+jjyn yjj <					+		= ":
				2		2

Значит, последовательность fxn +yng сходится и nlim (xn +yn) = x+y.
!1	"
2) Возьмем произвольное " > 0. Обозначим "0 = min f		;	1g.
	jjxjj + j j + 1

Тогда найдутся номера N1; N2 такие, что при всех n N1 выполняется jjxn xjj < "0 и при всех n N2 выполняется j n j < "0. Обозначим N = max fN1; N2g. При всех n N выполняется

jj nxn xjj = jj( n )x + (xn x) + ( n )(xn x)jj

j n j jjxjj+j j jjxn xjj+j n j jjxn xjj < "0 jjxjj+j j "0 +"20 =

"

= "0 (jjxjj + j j + "0) jjxjj + j j + 1 (jjxjj + j j + 1) = ":

Значит, последовательность f nxng сходится и lim nxn = x.

n!1

Определение 7.10. Пусть L – линейное нормированное пространство. Множество M L называется ограниченным, если существует такое число " > 0, что для всех x 2 M выполняется jjxjj ".

Определение 7.11. Последовательность fxng элементов линейного нормированного пространства L называется ограниченной, если существует такое число " > 0, что для всех n 2 N выполняется jjxnjj ".

Теорема 7.3. Сходящаяся последовательность fxng элементов линейного нормированного пространства L является ограниченной.

Доказательство. Так как fxng сходится, то для числа 1 найдется номер N 2 N такой, что при всех n N справедливо неравенство jjxn xjj < 1. Поэтому при всех n N имеем jjxnjj = jjxn x + xjj

38

jjxn xjj + jjxjj < 1 + jjxjj. Обозначим через " наибольшее из чисел jjx1jj, ..., jjxn 1jj, 1 + jjxjj. Тогда " > 0 и при всех n 2 N выполняется jjxnjj ", то есть последовательность fxng ограничена.

В одном и том же линейном пространстве можно задать различные нормы, поэтому иногда, чтобы указать какая именно норма выбрана, вместо L пишут (L; jjxjj). Если же утверждения верны для линейного пространства с произвольно выбранной нормой, то будем его обозначать просто L.

Пример. Рассмотрим множество Rn всех упорядоченных наборов ( 1; :::; n) из n вещественных чисел со следующими операциями сложения и умножения на вещественное число:

( 1; :::; n) + ( 1; :::; n) = ( 1 + 1; :::; n + n);

( 1; :::; n) = ( 1; :::; n):

Это пространство – n-мерное вещественное линейное пространство. Нулем этого пространства является элемент 0 = (0; :::; 0), одним из базисов – система (1; 0; :::; 0), (0; 1; :::; 0), ..., (0; 0; :::; 1).

В этом линейном пространстве можно задать различные нормы. Например,

jj

( 1

; :::; n )jj

=pj

1j+ ::: + j

;nj

2 ;

( ; :::; )

=

2 + ::: +

jj

1

n jj1

j 1j

j nj

jj( 1

; :::; n)jj1

= 1

k

n j kj:

max

Легко проверить, что в каждом из этих трех случаев аксиомы нормы выполняются.

Ниже для каждой из этих трех норм изображены "-окрестности нуля в двумерном пространстве R2:

p

1) для нормы jj( 1; 2)jj = j 1j2 + j 2j2 "-окрестность нуля изображена на рис. 7.1,

2)для нормы jj( 1; 2)jj = j 1j + j 2j на рис. 7.2,

3)для нормы jj( 1; 2)jj = maxfj 1j; j 2jg на рис. 7.3.

39

1 k n

max

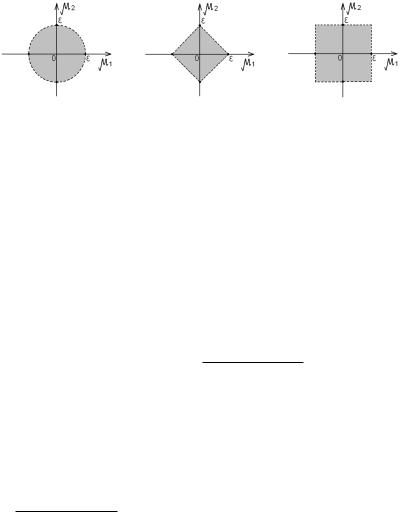
Рис. 7.1

Рис. 7.2

Рис. 7.3

Пример. Для комплексного пространства аналогично определяется множество Cn всех упорядоченных наборов ( 1; :::; n) из n комплексных чисел со следующими операциями сложения и умножения на комплексное число:

( 1; :::; n) + ( 1; :::; n) = ( 1 + 1; :::; n + n);

( 1; :::; n) = ( 1; :::; n):

Это пространство – n-мерное комплексное линейное пространство. Нулем этого пространства является элемент 0 = (0; :::; 0), одним из базисов – система (1; 0; :::; 0), (0; 1; :::; 0), ..., (0; 0; :::; 1).

В этом линейном пространстве также можно задать различные нормы. Например,

p

jj( 1; :::; n)jj = j 1j2 + ::: + j nj2 ; jj( 1; :::; n)jj1 = j 1j + ::: + j nj;

jj( 1; :::; n)jj1 = j kj:

Здесь также легко проверить, что в каждом из этих трех случаев аксиомы нормы выполняются.

Часто, если говорят о нормированном пространстве Rn (или Cn) без указания нормы, то подразумевается именно норма jj( 1; :::; n)jj =

p

= j 1j2 + ::: + j nj2 . Как будет показано дальше, для вопросов сходимости последовательностей, их пределов и т.д. не имеет значения, какая норма выбрана в пространстве Rn (или Cn).

Нам понадобится критерий компактности подмножества пространства Rn (Cn).

Теорема 7.4. Для того чтобы множество A Rn ( A Cn) было компактом, необходимо и достаточно, чтобы A было замкнутым и

40