Медведева Основы теории множеств и теории отображений 2011

попарно различных точек множества A, сходящаяся к a.

Доказательство. Пусть a – предельная точка множества A. Тогда окрестность O1(a) содержит бесконечно много точек из A. Выберем одну из точек множества O1(a) \ A и обозначим ее a1. Множество

O1 (a) также содержит бесконечно много точек из A. Поэтому можно

2

выбрать в множестве O1 (a)\A точку a2, отличную от a1. И так далее.

2

Множество O 1 (a) \ A содержит бесконечно много точек, и, значит, в

n

нем можно выбрать точку an, отличную от ранее выбранных точек a1, a2,..., an 1.

Выбирая таким образом точки a1, a2,..., an,..., получим последовательность fang1n=1 попарно различных точек множества A, причем

для всякого n 2 N имеем an 2 On (a), то есть (an; a) <	1		, а значит,
	n
1

lim an = a.

n!1

Пусть теперь последовательность fang1n=1 попарно различных точек множества A сходится к a. Тогда для любого " > 0 существует N 2 N такое, что при всех n N выполняется (an; a) < ". Это означает, что "-окрестность точки a содержит бесконечно много точек an 2 A. Поскольку положительное " произвольно, то a – предельная точка множества A.

Из теоремы 4.1 и определения 3.8 следует теорема 4.2.

Теорема 4.2. Множество A замкнуто тогда и только тогда, когда для всякой точки a 2 A существует последовательность fang точек множества A, сходящаяся к a.

Определение 4.2. Пусть (M1; 1) и (M2; 2) – метрические пространства. Отображение f : M1 ! M2 называется непрерывным в точке a 2 M1, если для любого " > 0 существует > 0 такое,что для всех x 2 M1, удовлетворяющих условию 1(x; a) < , выполняется неравенство 2(f(x); f(a)) < ".

Напомним, что 1 расстояние (метрика) в пространстве M1, а2 расстояние (метрика) в пространстве M2.

Если отображение f : M1 ! M2 непрерывно во всех точках множества M1, то говорят, что f непрерывно на M1.

Теорема 4.3. Отображение метрических пространств f : M1 ! M2 непрерывно в точке a 2 M1 тогда и только тогда, когда для всякой последовательности fang сходящейся к a, соответствующая последовательность ff(an)g сходится к f(a).

Доказательство. Пусть f непрерывно в точке a и последовательность fang сходиться к a в пространстве (M1; 1). Возьмем про-

21

извольное " > 0 и зафиксируем его. В силу непрерывности в точке a отображения f для этого " существует > 0 такое, что для всех x 2 M1, удовлетворяющих условию 1(x; a) < , выполняется неравенство 2(f(x); f(a)) < ". Поскольку fang сходится к a, то для этого числа найдется N 2 N такое, что при всех n N справедливо неравенство 1(an; a) < . Тогда при всех n N выполняется 2(f(an; f(a)) < ". Следовательно, по определению, последовательность ff(an)g сходится к f(a) в пространстве (M2; 2).

Пусть теперь для всякой последовательности fang, сходящейся к a, соответствующая последовательность ff(an)g сходится к f(a). Предположим при этом, что отображение f не является непрерывным в точке a. Тогда найдется " > 0 такое, что для всякого > 0 существует точка x 2 M1, удовлетворяющая условиям 1(x; a) < и 2(f(x); f(a)) ".

Следовательно, для каждого n = n1 , n 2 N, найдется точка xn 2 M1,

1

для которой 1(xn; a) < n, и при этом 2(f(xn); f(a)) ". Это означает, что последовательность fxng сходится к a, и при этом последовательность ff(xn)g не сходится к f(a). Противоречие. Поэтому f непрерывно в точке a.

Теорема 4.4. Пусть даны три метрических пространства (M1; 1), (M2; 2), (M3; 3) и отображение f : M1 ! M2 непрерывно в точке a 2 M1, а отображение g : M2 ! M3 непрерывно в точке b = f(a). Тогда композиция отображений g f : M1 ! M3 непрерывна в точке a.

Доказательство. Возьмем произвольное " > 0. Поскольку g непрерывно в точке f(a), то для этого " найдется число > 0 такое, что для всех y 2 M2, удовлетворяющих условию 2(y; f(a)) < , выполняется неравенство 3( g(y); g(f(a)) ) < ". Поскольку f непрерывно в точке a, то для этого найдется число > 0 такое, что для всех x 2 M1, удовлетворяющих условию 1(x; a) < , выполняется неравенство 2(f(x); f(a)) < , и, значит, 3( g(f(x)); g(f(a)) ) < ". Отсюда следует непрерывность отображения g f.

Теорема 4.5. Для того чтобы отображение метрических пространств f : M1 ! M2 было непрерывным на M1, необходимо и достаточно, чтобы прообраз f 1(U) всякого открытого множества U M2 был открытым.

Доказательство. Пусть f непрерывно на M1. Рассмотрим произвольное открытое множество U M2. Если a 2 f 1(U), то f(a) 2 U

22

и, в силу открытости множества U, существует "-окрестность O"(f(a)) U. Поскольку f непрерывно в точке a, то для этого " > 0 найдется > 0 такое, что при всех x 2 M1, удовлетворяющих условию

1(x; a) < , выполняется 2(f(x); f(a)) < ". Иначе говоря, O (a)f 1( O"(f(a)) ). Поскольку O"(f(a)) U, то O (a) f 1(U). Итак,

каждая точка a множества f 1(U) принадлежит этому множеству вместе с некоторой -окрестностью O (a). Это и означает, что множество f 1(U) – открытое.

Пусть теперь прообраз f 1(U) всякого открытого множества U M2 является открытым. Рассмотрим произвольную точку a 2 M1 и произвольное " > 0. Окрестность O"(f(a)) – открытое множество. Поэтому множество f 1( O"(f(a)) ) также открыто. Следовательно, точка a принадлежит множеству f 1( O"(f(a)) ) вместе с некоторой -окрестностью O (a). То есть, из условия 1(x; a) < следует 2(f(x); f(a)) < ". Значит, f непрерывно в каждой точке a 2 M1.

Поскольку дополнение открытого множества замкнуто (см. теорему 3.4) и прообраз дополнения равен дополнению прообраза (см. теорему 2.4), то отсюда следует теорема 4.6, аналогичная предыдущей.

Теорема 4.6. Для того чтобы отображение метрических пространств f : M1 ! M2 было непрерывным на M1, необходимо и достаточно, чтобы прообраз f 1(U) всякого замкнутого множества U M2 был замкнутым.

ГЛАВА 5. ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА

Определение 5.1. Последовательность fang точек метрического пространства (M; ) называется фундаментальной, если для любого " > 0 существует натуральное число N = N(") такое, что при всех n N, m N выполняется неравенство (an; am) < ".

Утверждение 5.1. Всякая сходящаяся последовательность элементов метрического пространства является фундаментальной.

Доказательство. Пусть fang сходится к элементу a в пространстве (M; ). Тогда для всякого " > 0 существует такое число N = N("),

что при всех k N выполняется (ak; a) < 2" . Из неравенства тре-

угольника следует, что (xn; xm) (xn; a) + (a; xm) < 2" + 2" = " при всех n N, m N. Значит, последовательность fang фундаменталь-

на.

Однако существуют метрические пространства в которых некоторые фундаментальные последовательности не являются сходящимися.

23

Утверждение 5.2. Если фундаментальная последовательность fang1n=1 содержит сходящуюся к точке a подпоследовательность, то она сама сходится к тому же пределу.

Доказательство. Зафиксируем произвольное " > 0. В силу фундаментальности последовательности fang1n=1 для этого " существует

такое число N1 = N1("), что при всех n N1, m N1 выполняется неравенство (an; am) < 2" .

Пусть подпоследовательность fakn g1n=1 сходится к a. Тогда суще-

ствует такое число N2 = N2("), что при всех n N2 выполняется

(akn ; a) < 2" .

Обозначим N = max fN1; N2g. Имеем при всех n N:

" "

(an; a) (an; akn ) + (akn ; a) < 2 + 2 = ":

Следовательно, последовательность fang1n=1 сходится к a.

Определение 5.2. Если в пространстве (M; ) любая фундаментальная последовательность сходится, то это пространство называется полным.

Пример. Пусть M = (0; 1], ( ; ) = j j. Последовательность точек fxng1n=1 = fn1 g1n=1 фундаментальна, но не сходится ни к одной точке из (0; 1]. Поэтому это метрическое пространство не является полным.

Пример. Пространство R с метрикой ( ; ) = j j полное (его полнота известна из курса математического анализа).

s

	n
Пример. Пространство Rn с метрикой ( ; ) =	kP
	( k k)2
	=1

полное (его полноту можно доказать, используя полноту R). Пример. Пространство C[a; b] множество всех непрерывных на

[a; b] функций f : [a; b] ! R c метрикой (f; g) = max jf(x) g(x)j

x2[0;1]

полное. Его полнота следует из теоремы математического анализа о том, что равномерно сходящаяся последовательность непрерывных на [a; b] функций сходится к непрерывной функции.

Теорема 5.1 (принцип вложенных шаров). Для того чтобы метрическое пространство было полным, необходимо и достаточно, чтобы в нем всякая последовательность замкнутых вложенных друг в друга шаров, радиусы которых стремятся к нулю, имела непустое пересечение.

24

при всех n nm+1.

при всех n n2. Обозначим через K2 замкнутый шар

Доказательство. Необходимость. Пусть (M; ) – полное метрическое пространство, K1 K2 ::: – вложенные друг в друга замкнутые шары, причем Kn – замкнутый шар с центром an и радиусом rn,

lim rn = 0. Возьмем произвольное " > 0. Для этого " найдется такое

n!1

число N, что rn < 2" . Поскольку шары вложены друг в друга, то все центры шаров aN , aN+1, aN+2,... принадлежат шару KN . Следовательно, при всех n N и m N имеем (an; am) (an; aN )+ (aN ; am)rN + rN < 2" + 2" = = ". Значит, последовательность точек fang фундаментальна. Поскольку (M; ) – полное пространство, то fang

сходится, то есть существует элемент a 2 M такой, что a = lim an.

n!1

Если из последовательности fang можно выбрать подпоследовательность попарно различных точек, то элемент a является предельной точкой каждого шара Kn, n 2 N, поскольку все центры шаров, начиная с n-го, принадлежат шару Kn. Так как каждый шар Kn замкнут, а значит, содержит все свои предельные точки, то точка a

	1
	nT
принадлежит каждому шару Kn, n 2 N. Поэтому a 2	=1 Kn.

Если же из последовательности fang нельзя выбрать подпоследовательность попарно различных точек, то это означает, что, начиная с некоторого номера, центры шаров совпадают друг с другом, и тогда

	1
	nT
также a 2	=1 Kn.

1

T

Итак, получили, что Kn не является пустым множеством.

n=1

Достаточность. Пусть всякая последовательность замкнутых вложенных друг в друга шаров, радиусы которых стремятся к нулю, имеет непустое пересечение. Возьмем произвольную фундаментальную последовательность fang элементов метрического пространства (M; ). Докажем, что она сходится. В силу фундаментальности мы можем вы-

1

брать такую точку an1 нашей последовательности, что (an; an1 ) < 2

при всех n n1. Обозначим через K1 замкнутый шар радиуса 1 с центром в точке an1 . Далее, выберем такую точку an2 , что n2 > n1 и

1

(an; an2 ) < 22

радиуса 12 с центром в точке an2 . Пусть точки an1 , an2 , ..., anm уже выбраны. Тогда точку anm+1 выберем так, чтобы выполнялись усло-

1

вия: nm+1 > nm > ::: > n1 и (an; anm+1 ) < 2m+1

25

Легко убедится, что

Тогда (anm ; a)

1

Через Km+1 обозначим замкнутый шар радиуса 2m с центром в точке

anm+1 . И так далее. Получили последовательность замкнутых шаров K1 K2 :::, радиусы которых стремятся к нулю. По предположению

1	1
m=1 Km 6= ;, то есть существует точка a 2 M такая, что a 2	=1 Km.
T	mT

1

2m 1 для всякого m 2 N. Значит, подпоследователь-

ность an1 , an2 , ..., anm , ... сходится к точке a. В силу утверждения 5.2 последовательность fang сходится к той же точке a.

Итак, в пространстве (M; ) любая фундаментальная последовательность сходится. Поэтому это пространство является полным.

Если в этой теореме одно из условий: полноту пространства, замкнутость шаров, условие того, что они вложены или стремление радиусов к нулю, убрать, то получившееся утверждение будет неверным.

Пример. Пространство (M; ), где M = (0; 1], ( ; ) = j j, не является пол-

ным. Возьмем в этом пространстве замкнутые

шары Kn = fx 2 M : jx 21n j 21n g = (0; n1 ]. Они вложены, их радиусы стремятся к нулю,

однако их пересечение пусто.						Рис. 5.1
Пример. Пространство R с метрикой	( ; )							j 1полное.
		1		= j1
Возьмем открытые шары On = fx 2 R : jx			j <			g = (0; n ). Они
		2n			2n

вложены друг в друга, их радиусы стремятся к нулю, но их пересечение пусто.

Пример. Пусть M = N множество всех натуральных чисел. Обо-

значим (m; n) =	1 + m+1 n ;	если m 6= n:
	0;	если m = n;

(N; ) метрическое пространство. Пусть fxng фундаментальная последовательность элементов этого пространства. Тогда для этой последовательности найдется такой номер N 2 N, что все xn, начиная с этого номера N, равны, то есть при всех n N элементы xn = xN . Отсюда следует, что последовательность fxng сходится к элементу xN . Поскольку всякая фундаментальная последовательность сходится, то

пространство (N; ) полное.

Возьмем шар Kn = fm 2 N : (m; n) 1 + 21n g радиуса 1 + 21n с центром в точке n, n 2 N. Тогда Kn = fn; n + 1; n + 2; :::g. Шары Kn

замкнуты (см. замечание в конце главы 3), вложены друг в друга, но

26

	1
	nT
их радиусы не стремятся к нулю и пересечение	=1 Kn = ;.

Докажем теперь важную теорему об отображении полного метрического пространства. Сформулируем сначала следующее определение.

Определение 5.3. Отображение f : M ! M метрического пространства в себя называется сжимающим, если существует такое число , что 0 < < 1 и при всех x 2 M, y 2 M выполняется

(f(x); f(y)) (x; y):

Утверждение 5.3. Сжимающее отображение f : M ! M непрерывно на M.

Доказательство. Рассмотрим произвольную точку a 2 M. Для каждого " > 0 возьмем = " . При всех x 2 M, удовлетворяющих условию (x; a) < , выполняется (f(x); f(a)) (x; a) < = = " = ". Следовательно, отображение f непрерывно в каждой точке a 2 M.

Теорема 5.2 (принцип сжимающих отображений). Сжимающее отображение f : M ! M полного метрического пространства в себя имеет и притом единственную неподвижную точку, то есть такую точку a 2 M, что f(a) = a.

Доказательство. Пусть a0 – произвольная точка из M. Положим a1 = f(a0), a2 = f(a1), ..., an = f(an 1), ... . Покажем, что последовательность fang фундаментальна. Действительно, (для определенности полагая m n) имеем

(an; am)= (f(an 1); f(am 1)) (an 1; am 1) ::: n (a0; am n)

n( (a0; a1) + (a1; a2) + ::: + (am n 1; am n) )

n (a0; a1)( 1 + + 1 + ::: + m n 1 ) n (a0; a1) 1 1 :

Возьмем произвольное " > 0. Выбрав для этого " натуральное чис-

ло, например N = N(") = [ log "(1 ) ]+1, получим при всех n N,

1+ (a0;a1)

m N неравенство (an; am) < ". Значит, fang фундаментальна. Поскольку пространство M полное, то последовательность fang сходится,

27

то есть существует lim an = a 2 M. В силу утверждения 5.3 отоб-

n!1

ражение f непрерывно. Поэтому f(a) = f( lim an) = lim f(an) =

n!1 n!1

= lim an+1 = a.

n!1

Итак, существование неподвижной точки доказано. Докажем ее единственность. Если f(a) = a и f(b) = b, то (a; b) = (f(a); f(b))

(a; b). Значит, (a; b) (1 ) 0. Так как < 1, то (a; b) = 0, то есть a = b.

Замечание. Если отображение f : M ! M полного метрического пространства в себя обладает лишь свойством (f(x); f(y)) < (x; y) для всех x 6= y, то неподвижной точки может и не быть.

Пример. Для метрического пространства (M; ), где M = [1; +1),

(x; y) = jx yj, и отображения f : M ! M, f(x) = x + x1 , имеем(f(x); f(y)) = jx+ x1 y y1 j < jx yj = (x; y) при всех x 6= y множества

[1; +1). Однако неподвижной точки нет, так как f(x) = x + x1 6= x для всякого x 2 [1; +1).

Принцип сжимающих отображений используется в различных разделах математики: в теории дифференциальных уравнений, теории интегральных уравнений и т.д.

ГЛАВА 6. КОМПАКТНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА

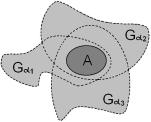
Пусть A M. Покрытием множества A в метрическом пространстве (M; ) называется любое семейство открытых множеств, объединение которых содержит A.

Определение				6.1. Множество A
называется компактным или компак-
том, если любое его покрытие содер-
жит конечное подпокрытие.
Иначе говоря, если объединение от-
крытых множеств				G содержит мно-
	A
жество		, то	можно выбрать конечное
				S
число множеств G 1 , ..., G m из этого
семейства так, чтобы A G 1 [:::[G m .					Рис. 6.1

Определение 6.2. Метрическое пространство (M; ) называется компактом, если множество M – компакт.

28

Пример. Приведем без доказательства следующее утверждение: всякий отрезок [a; b] R (метрика ( ; ) = j j) – компакт. Это утверждение известно в анализе как лемма Гейне–Бореля.

Пример. Пространство R (метрика ( ; ) = j j) не является

1

S

компактом, так как ( n; n) = R, но из покрытия R интервалами

n=1

( n; n), n 2 N, нельзя выбрать конечное подпокрытие.

Пример. Интервал (a; b) R (метрика ( ; ) = j j) не является компактом, поскольку для открытых множеств G = (a + ; b )

S		S
имеем	G =	(a + ; b ) = (a; b), но из покрытия

2(0; a+2 b ) 2(0; a+2 b )

(a; b) множествами G , 2 (0; a+2 b ), нельзя выделить конечное подпокрытие.

Пример. В главе 7 будет доказано, что всякое замкнутое, ограниченное множество из Rn (в Rn выбрана метрика ( ; ) =

p

= ( 1 1)2 + ::: + ( n n)2 ) является компактом. Поэтому, например, все замкнутые шары в Rn компактны. В частности (см. пример выше), все отрезки [a; b] R компакты.

Теорема 6.1. Замкнутое подмножество компактного метрического пространства компактно.

Доказательство. Пусть M – компакт, A M, A замкнуто. Тогда дополнение MnA – открытое. Если семейство множеств fG g, где все G – открытые, является покрытием множества A, то

S

M = A [ (MnA) = G [ (MnA). Значит, семейство открытых мно-

жеств fG g с добавленным открытым множеством MnA является покрытием множества M. В силу компактности M из него можно выделить конечное подпокрытие, то есть G 1 [ ::: [ G m [ (MnA) = M. Тогда A = Mn(MnA) G 1 [ ::: [ G m . Получили, что всякое покрытие множества A содержит конечное подпокрытие. Следовательно, A – компакт.

Теорема 6.2. Компактное подмножество метрического пространства замкнуто.

Доказательство. Пусть (M; ) – метрическое пространство, K M, K – компакт. Если K = M, то K – замкнутое множество (по определению). Если K 6= M, то рассмотрим произвольную точку a 2 (MnK). Для всякой точки x 2 K возьмем "-окрестность O"(x)(x), где " = "(x) =

29

= (	a;x)	6= 0. Тогда K	[ O"(x)(x). Поскольку K – компакт, то
	3

x2K

из покрытия fO"(x)(x)g можно выделить конечное подпокрытие, то есть найдутся точки x1, ...,xm множества K такие, что множество

K O"1 (x1) [ ::: [ O"m (xm). Обозначим = minf"1; :::; "mg. Докажем, что -окрестность O (a) (MnK). Действительно, если элемент

y 2 O (a), то (y; a) < "1, при этом из неравенства треугольника следует (a; x1) (a; y) + (y; x1). Поэтому расстояние (y; x1)

(a; x1) (a; y) = 3"1 (a; y) > 3"1 "1 = 2"1. Отсюда y 62O"1 (x1). Аналогично получим y 62O"2 (x2), ..., y 62O"m (xm), и, значит, y 62K.

Следовательно, O (a) (MnK). Итак, всякая точка a принадлежит множеству MnK вместе с некоторой -окрестностью O (a), то есть множество MnK открыто. Поэтому K замкнуто.

Теорема 6.3. Если метрическое пространство компактно, то из всякой последовательности его точек можно выделить сходящуюся подпоследовательность (к точке из этого пространства).

Доказательство. Пусть (M; ) – компактное метрическое пространство. Предположим, что существует последовательность fang1n=1 точек этого пространства из которой нельзя выбрать сходящуюся под-

	1
последовательность. Тогда каждое из множеств Ak =	nS
	an, k 2 N,
	=k

состоит из бесконечного числа точек и не имеет предельных точек.

			1		1
При этом k=1 Ak				= ; ( иначе элемент a 2 k=1 Ak		в последовательно-
сти		a	1		раз, что противоречит от-
	f	n	Tвстречается бесконечно много		T
			gn=1			N
сутствию сходящихся подпоследовательностей) и						kT
						Ak 6= ; при всех
						=1

N

T

N 2 N (поскольку Ak faN ; aN+1; :::g). Поскольку каждое множе-

k=1

ство Ak, k 2 N, не имеет предельных точек, то все Ak замкнуты (следует из определения замкнутого множества). Поэтому их дополнения MnAk, k 2 N, являются открытыми множествами. С помощью прин-

1	1
\	k[
ципа двойственности получим M = Mn; = Mn( Ak) =	(MnAk),
k=1	=1

то есть семейство открытых множеств fMnAkg образует покрытие множества M. Так как M компакт, то из этого покрытия можно выбрать конечное подпокрытие, а значит, для некоторого m 2 N вы-

30