Мишулина Основы теории вероятностей 2011

Таким образом, рассматривается композиция одинаковых показательных распределений. Вычисление плотности вероятности случайной величины Y приводит к следующему результату:

f (x)	( x)n 1	e x , x > 0 .	(4.23)
	(n 1)!

Наиболее просто этот результат может быть получен с использованием характеристической функции показательного закона распределения.

Распределение вероятностей (4.23) называют гамма-

распределением с целочисленным параметром n. Обычно плот-

ность распределения f (x) (4.23) записывают в следующей форме:

f (x)	( x)n 1	e x , x > 0,	(4.24)
	Г(n)
где Г(n) – гамма-функция, определяемая выражением:
Г(g) u g 1e u du .			(4.25)
0
Для целочисленного аргумента n > 0 справедливо равенство
Г(n 1) n!,			(4.26)

которое использовано при написании выражения (4.24). Отметим, что для гамма-функции справедливо рекуррентное выражение:

(g) (g 1) (g 1), g 0.

Кроме того, (1) 1 и (1/ 2) .

Для расчета математического ожидания и дисперсии гаммараспределения воспользуемся известными значениями характери-

стик показательного распределения случайных величин X i , i 1, n

(см. § 16, пример 2.9): mXi 1/ ; d Xi 1/ 2 . Поскольку Y являет-

ся композицией независимых случайных величин X i , i 1, n , по-

лучаем	следующие	числовые		характеристики	гамма-
распределения:
	M[Y ] n / ,		D[Y ] n / 2 .		(4.27)
					181

Пусть случайные величины Y 1 и Y 2 независимы и имеют гам-

ма-распределения с одним и тем же значением параметра и целочисленными параметрами n1 и n2 соответственно. Рассмотрим

случайную величину Z = Y 1+Y 2 . Несложно установить, что в этом

случае Z может быть представлена как сумма (n1 + n2) независимых слагаемых, распределенных по показательному закону, и, следовательно, имеет гамма-распределение с целочисленным параметром (n1 + n2). Это означает, что гамма-распределение обладает композиционной устойчивостью.

Заменим в выражении (4.24) для плотности распределения вероятностей целочисленный параметр n на произвольный действительный параметр > 0. В этом случае будет получена функция

f (x)	( x) 1	e x ,	x > 0, > 0,	(4.28)
	Г( )

которая обладает свойствами плотности распределения вероятностей. Полученное распределение носит название гамма-

распределения с действительным параметром ( > 0).

Рассмотрим математическое ожидание для гамма-распределения с действительным параметром > 0:

m x f (x)

0

( x)( 1) 1

( 1)

0

		( x)
	dx				e x dx
	0	( )				(4.29)
	e x dx
				f 1 (x) dx			.
				0

Здесь нижний индекс и ( + 1) в обозначении плотности распределения вероятностей указывает на параметр гаммараспределения.

Аналогично можно получить выражение для дисперсии

d / 2 .

(4.30)

Формулы (4.29), (4.30) обобщают приведенные ранее формулы (4.27) для числовых характеристик гамма-распределения с целочисленным параметром.

182

Для гамма-распределения с действительным параметром также справедливо свойство композиционной устойчивости, отмеченное ранее для гамма-распределения с целочисленным параметром. Оно состоит в том, что если Y 1 и Y 2 независимы, характеризуются об-

щим значением параметра и имеют гамма-распределения с параметрами 1 и 2 , то их сумма Z = Y 1 +Y 2 имеет гамма-

распределение с параметром ( 1 + 2 ).

Рассмотрим частный случай гамма-распределения при 1 :

2

( x)

1

f 1 (x)

2

e x

, x > 0.

1

2

2

равенство Γ

Учитывая приведенное выше

1

и полагая

2

1

, получим

2 2

1

x

f 1

(x)

e 2 2 ,

x > 0.

2 x

2

Приведенное выражение

для

f 1 (x)

совпадает

с

плотностью

2

распределения вероятностей (4.20) для закона Рэлея. Таким образом, распределение Рэлея является частным случаем гамма-

распределения при значении действительного параметра 12 .

§ 34. Распределение χ 2

Рассмотрим сумму квадратов n независимых нормально распре-

						с параметрами 0, 2
деленных случайных величин X	i	,	i 1, n ,
(нормальное распределение вероятностей N(0, ) ):
n			n
X X i2			Y i .			(4.31)
i 1			i 1
						183

Здесь Yi = X i2 , i 1, n , независимы и подчинены закону Рэлея, являющемуся частным случаем гамма-распределения с параметрами

		1	и 1 .
		2
2			2

Используя приведенное в предыдущем параграфе свойство композиционной устойчивости гамма-распределения, приходим к выводу, что случайная величина X (4.31) имеет гамма-распределение

с параметром 2n :

				n
		x				1					x
				2
f (x)											2	2
										e			, x > 0.	(4.32)
					n
							n
		2
	(2		) 2
							2

Распределение (4.32) носит название 2 -распределения с n сте-

пенями свободы. Множитель 2

является масштабным и в стати-

стических таблицах полагается равным единице (

1

):

2

n

1

x

f (x)

x 2

e 2 ,

x > 0.

(4.33)

n

n

2

2

2

На основании (4.29), (4.30)

при

n

,

1

получаем мате-

2

2

матическое ожидание и дисперсию 2 -распределения:

m M[ 2 ] n ,

D[ 2 ] 2n .

(4.34)

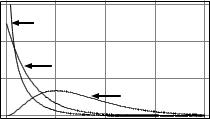
На рис. 4.3 приведена

серия

графиков плотности

2 -распределения. Для n > 2 плотность распределения является унимодальной функцией с максимумом при x n 2 .

184

fX(x)
0,6
	n=1
0,4
	n=2
0,2
			n=6
0
0	4	8	12	16	x
Рис. 4.3. Плотность χ2-распределения вероятностей
	с n степенями свободы

Рассмотрим статистическую модель, в которой возникает распределение 2 с n степенями свободы. Допустим, что производятся n независимых наблюдений нормально распределенной слу-

чайной величины X с параметрами m и 2 . Можно интерпретировать этот эксперимент как наблюдение n независимых случайных

величин	X i ,	i 1, n , с				одинаковыми законами					распределения
N(m, σ2).	Проведем их нормирование:
		~					X i m
					X i			, i 1, n ,
и рассмотрим случайную величину Z:
								n ~
							Z X i2 .				(4.35)
								i 1
		~
Поскольку		X i , i 1, n , имеют распределение N(0, 1) и незави-

симы, случайная величина Z распределена по закону 2 с n степенями свободы.

§ 35. Распределение χ

Рассмотрим случайную величину Z, которая распределена по закону 2 с n степенями свободы, т.е. имеющую гамма-

185

распределение с параметрами 12 , 2n (4.33). Рассмотрим слу-

чайную величину Y

Z . Вычислим интегральный закон распре-

деления вероятностей FY ( y) , y > 0:

y2

FY ( y) P(

Z

y) P[Z y2 ] fZ (z) dz .

0

Тогда

y2

dFY ( y)

2 y

n 1

2

f ( y)

2 y f

( y 2 )

e

, y > 0. (4.36)

2

Y

Z

2

n / 2

dy

Распределение вероятностей (4.36) случайной величины Y назы-

вается -распределением.

При n = 3 -распределение называют распределением Максвелла. На основании формулы (4.36) и равенства n2 / 2 плотность распределения Максвелла определяется выражением:

							y2 e	y2
	f	Y	( y)		2			2	,	y > 0.

Принимая во внимание сделанное в конце предыдущего пара-

графа замечание	(4.35) относительно математической модели
2 -распределения,	можно дать -распределению следующую

геометрическую интерпретацию. Распределению подчиняется

длина радиуса-вектора в евклидовом пространстве, если проекции вектора на оси координат случайны, независимы и одинаково распределены по нормальному закону N(0, 1).

В математической статистике применяют -распределение, от-

масштабированное с помощью постоянного коэффициента 1/ n , где n – число степеней свободы распределения. Случайная величи-

на Y Y /

n подчинена распределению /

n с плотностью

1

n y2

n

y)n 1

fY ( y)

n fY ( n y)

2 .

2n (

e

(4.37)

2

n

2

186

В выводе выражения (4.37) применено доказанное ранее правило расчета плотности распределения вероятностей случайной величины после ее линейного преобразования.

§36. Функция распределения частного. Распределение Стьюдента

Определим случайную величину T как частное от деления двух независимых случайных величин:

	T	X	,	(4.38)
		Y

где X – нормированная нормально распределенная случайная величина N(0, 1), а Y имеет / n -распределение с n степенями сво-

боды. Предполагается, что случайные величины X и Y' независимы. Найдем выражение для функции распределения вероятностей

FT (t) :

X				f (x, y) dxdy ,
FT (t) P		t				(4.39)
Y				x	t
				y

где f(x, y) – совместная плотность распределения случайных величин X и Y'.

	y
				x/y = t
x/y < t
				x
		x/y <	t

Рис. 4.4. Иллюстрация к расчету функции распределения вероятностей частного от деления двух случайных величин

На рис. 4.4 показана область интегрирования в выражении (4.39), которая состоит из двух частей. Это позволяет провести дальнейшие преобразования выражения (4.39):

187

yt

0

FT (t) dy f (x, y) dx dy f (x, y) dx .

0 yt

После дифференцирования по переменной t получим выражение

для плотности распределения	fT (t) :
	0
fT (t) y f ( yt, y) dy y f ( yt, y) dy .
0
Поскольку случайные величины X и Y' независимы, можно запи-
сать:
	0
fT (t) y f X ( yt) fY ' ( y)	dy y f X ( yt) fY ' ( y) dy .	(4.40)
0

Таким образом, получено выражение для плотности распределения частного от деления двух независимых случайных величин. После подстановки в выражение (4.40) функций плотности для распределений случайных величин X и Y' и интегрирования получим следующее выражение:

						n 1							t 2		n 1
																2
							2
f		(t)									1				.			(4.41)
	T			n
								n					n
				2

Распределение (4.41) носит название распределения Стьюдента с n степенями свободы, или t-распределения (William Sealy Gosset, псевдоним Student, 1876 – 1937, Англия). Заметим, что случайная

величина T может принимать любые действительные значения в интервале ( , ) .

Математическое ожидание случайной величины, распределенной по закону Стьюдента, равно нулю в силу симметрии плотности распределения вероятностей, а дисперсия для n > 2 равна n /(n 2).

При n = 1 плотность распределения (4.41) приводится к виду:

	fT (t)	1 1			.	(4.42)
		1 t 2

Это распределение вероятностей является частным случаем распределения Коши (2.39) при значениях параметров α = 0, β = 1. Функция распределения вероятностей FT (t) закона Коши (4.42)

определяется выражением:

188

F	(t) 1	1 arctg t .		(4.43)
T	2
Для случайной величины, распределенной по закону Коши, не су-
ществует математического ожидания, дисперсии и моментов более
высокого порядка.
f (x)
0,4		N(0, 1)
0,3
0,2
0,1
0			T5
-6 -4 -2 0		2	4	6 x
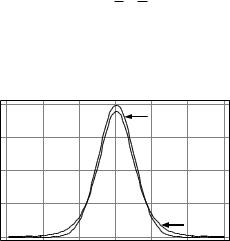
Рис. 4.5. Графики плотности распределения вероятностей
нормального закона N(0, 1) и закона Стьюдента T5

При увеличении числа n степеней свободы t-распределение приближается к нормальному распределению N(0, 1) (рис. 4.5).

§ 37. Распределение Фишера

Рассмотрим две независимые случайные величины X и Y, каж-

дая из которых имеет 2 -распределение с параметрами								n	и	n	2
								1
соответственно. Введем случайную величину Z:
Z	X	:	Y			X n2	.		(4.44)
	n		n	2		Y n
1					1

Случайная величина Z подчинена распределению Фишера (Ronald Aylmer Fisher, 1890 – 1962, Великобритания) с плотностью вероятности

			n1	1		n				1	(n1 n2 )
f (z) C	0	z 2		1		1	z			2	,	(4.45)
						n2

189

					1	(n			n				)						1 n
где	C				2		1				2								2 1
		0														n1		.
				1						1						n
					n							n
																	2
				2		1				2				2
	f (z)
	0,8
	0,6
	0,4
	0,2
		0

0 1 2 3 4 5 z

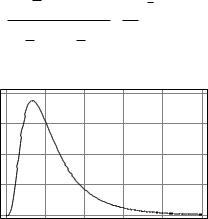
Рис.4.6. Плотность распределения вероятностей закона Фишера с параметрами n1 = n2 = 10

На рис. 4.6 приведен график плотности распределения вероятностей для закона Фишера, который обычно называют F-распределением и обозначают F (n1, n2 ) . Параметры n1 и n2 называются степенями свободы распределения Фишера. Отметим, что случайная величина 1/ Z распределена также по закону Фишера, но с обратным порядком следования параметров n2 и n1 , т.е. имеет распределение F (n2 , n1) .

Если n1 = n2 = n, то для любого n медиана распределения Фишера равна единице. Это означает, что семейство графиков функции распределения вероятностей для разных n пересекается в одной точке, в которой z = 1 и F(1) = 0,5 (рис. 4.7). Соответствующее семейство графиков плотности распределения вероятностей показано на рис. 4.8.

На графиках рис. 4.8 видно, что при увеличении чисел степеней свободы n1 и n2 плотность распределения f (z) концентрируется около значения z = 1.

190