[ Филиппов ] Теория упругости (лекции)

11

где Eэф =1−Eν2 - эффективный модуль Юнга. Как будет показано ниже, эта

постоянная возникает при решении задачи о распространении волн в тонких пластинах. При запрещенных смещениях всех четырех боковых граней ( εy = 0 ; εz = 0 ), система уравнений для продольных и поперечных

деформаций примет вид:

εx = E1 σx − Eν σy − Eν σz ;

εy = E1 σy − Eν σx − Eν σz = 0;

εz = E1 σz − Eν σx − Eν σy = 0 ,

откуда следует σy + σz =12−ννσx и

			ε		x	=	1	σ	x	,
							′
			E(1−ν)				Eэф
где величина	′				также называется эффективным модулем
			+ ν)(1− 2ν)
	Eэф = (1

Юнга. Как будет показано ниже, эта постоянная возникает при решении задачи о распространении волн в упругих непрерывных средах.

3.3. Деформация сдвига

	Деформации сдвига возникают под действием касательных сил - сил,
	направленных вдоль поверхности упругого тела (рис. 3.3).
	Рассмотрим квадратный в сечении брусок, к боковым
	граням которого приложены касательные силы G,	G
	равномерно распределенные по поверхностям граней.
	Сечение ABCD такого бруска и направления действия
	поверхностных сил представлены на рисунке 3.4.

Чтобы брусок находился в равновесии, внешние воздействия на него должны удовлетворять следующим двум условиям:

1.Сумма сил, действующих на брусок, равна нулю.

2.Сумма моментов сил, действующих на брусок, равна нулю.

Рис. 3.3

G

G

Рис. 3.4

12

Найдем изменения длин диагоналей AC и BD при сдвиговых деформациях бруска под действием приложенных касательных сил. Для этого используем уже изученные закономерности деформаций сжатия и растяжения тел.

Представим себе, что брусок с сечением ABCD является внутренней областью бруска квадратного сечения PQRT (рис. 3.5). Приложим к граням бруска PQRT силы

A

G

D

B

G

C

F = 2 G так, как это показано на рисунке 3.5.

При этом, длина бруска L, как легко показать,

останется неизменной, а на гранях внутреннего бруска возникнут касательные силы величиной G. Докажем это последнее утверждение.

Q

							Q
2 G	G		2 G	2		G	2	G
				2			2
							G'
	A	B			A		B
P	G	G	R				Рис. 3.6
	D	C
2 G	G		2 G			2 G	2 G
						2	2
	T						G'
	Рис. 3.5						Рис. 3.7

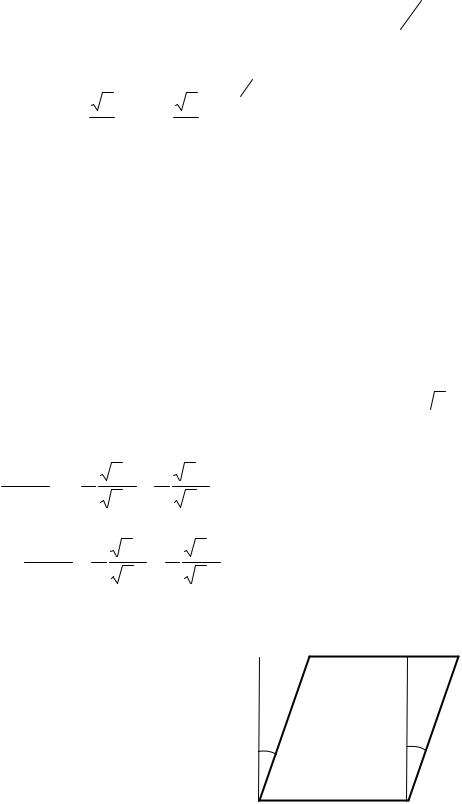
13

Глядя на рисунок 3.5, мысленно выделим брусок треугольного сечения AQB и рассмотрим силы, действующие на его грани (рис. 3.6). Так как этот брусок находится в равновесии, векторная сумма действующих на него сил

должна быть равна нулю. Отсюда, учитывая условие AQB = π	2	, из

треугольника сил, изображенного на рисунке 3.7, находим:

	′		2			2		2			2	12
G				G		+			G				=G ,
		=
			2					2

т.е. на грань AB треугольного бруска действует поверхностная сила, по абсолютной величине равная G . Очевидно, что на прилегающую грань AB бруска квадратного сечения ABCD должна действовать противоположно направленная поверхностная сила, по абсолютной величине также равная G , как и показано на рисунке 3.5.

Из рисунка 3.5 видно, что изменение длин отрезков AC и BD под действием сил, приложенных к боковым граням бруска PQRT, можно найти с использованием закона Гука и закона Пуассона. Обозначив S площадь боковой грани бруска с сечением ABCD, легко показать, что

площадь боковой грани бруска с сечением PQRT будет составлять 2 S . Отсюда следует:

	δ(AC)= −		1 2G −		ν 2G = −			(1+ ν)G
								E	S
	AC		E	2S	E	2S
									(3.1)
	δ(BD)	=		1 2G	+	ν 2G	=	(1+ ν)G
	BD		E 2S		E 2S			E	S

Таким образом, деформация сдвига может быть представлена как деформация сжатия-растяжения, и это обстоятельство позволяет связать степень сдвиговых деформаций с величиной коэффициента Пуассона и модуля Юнга.

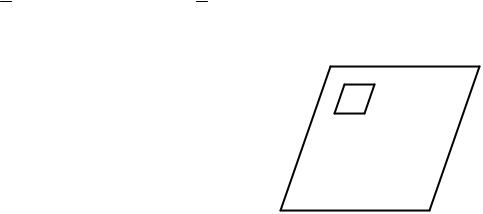
Рассмотрим сдвиговую деформацию бруска, показанного на рисунке 3.4, закрепив неподвижно его нижнюю грань

A B

θθ

D C

Рис. 3.8

14

(рис. 3.8). Зная из уравнений (3.1),

как

меняются

диагонали

четырехугольника

ABCD при сдвиговой деформации, найдем

d'

величину угла θ, характеризующего

θ

отклонение боковых граней от вертикали.

l

Обозначим l длину сторон ромба ABCD

π/2

на рисунке 3.8: AB=BC=CD=DA=l,

d

-

длину диагонали BD до деформации, и d' -

l

длину

этой

же

диагонали

в

деформированном бруске. До деформации

Рис. 3.9

сечение

бруска

представляло

собой

квадрат, поэтому

d 2 = 2l2 .

Величину

d′

можно найти из рисунка 3.9 с помощью теоремы косинуса:

′ 2

2

2

2

π

(d )

=l

+l

−2l

cos

2

+ θ

.

Преобразуем входящий в это выражение косинус с учетом малости угла θ:

	cos π + θ =sin(−θ)					≈ −θ,
	2
откуда следует
	θ =	(d′)2 − d 2			.
		d 2
Обозначив δd = δ(BD), получаем d′ = d +δd ,
θ =	(d′− d )(d′+ d )		≈	2d δd			= 2		δd	,
									d
	d 2			d 2

и с учетом (3.1) находим

θ = 21+Eν SG .

По аналогии с величиной σ - напряжением растяжения-сжатия, введем величину напряжения сдвига

15

g = GS ,

что позволяет записать формулу для угла θ в окончательном виде:

						θ =	1	g ,
							µ
	E
где µ =		- модуль сдвига.
	2(1+ ν)
Из условия 0 < ν <			1	следует:	E	<µ <	E .
			2		3		2

Оценим изменения сечения, длины и объема бруска при сдвиговых деформациях. Как было отмечено выше, длина бруска L при сдвиговых деформациях остается постоянной, а изменение площади сечения есть величина второго порядка малости относительно изменения длины диагонали ромба ABCD:

δS = S′− S = 12 [(d + δd )(d −δd )− d 2 ]= 12 (δd )2 ≈ 0 .

	Следовательно, изменение объема тела	A	B
	при сдвиговых деформациях является
	пренебрежимо малым:
	δV = LS′− LS ≈ 0 .
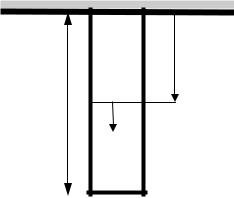
	Отметим в заключение, что сдвиговая
	деформация действительно является	D	C
	однородной: угол наклона боковых
	граней относительно нижней у любого		Рис. 3.8
	внутреннего элемента бруска одинаков
	(рис. 3.10) и составляет θ.

4. НЕОДНОРОДНЫЕ ДЕФОРМАЦИИ

Неоднородными называются такие деформации, при которых величина

ε = ∂∂ux не является постоянной по всему телу. Рассмотрим несколько примеров неоднородных деформаций.

16

4.1.Деформация под действием массовых сил

Рассмотрим стержень длиной l, сечением S, модулем Юнга E и с однородной плотностью ρ. Стержень закреплен верхним концом (рис. 4.1). Найдем распределение напряжений в стержне и его полное удлинение. На расстоянии x от точки подвеса на площади сечения S действует сила F, равная весу нижней части стержня длиной (l-x):

	Fx	= M x	g =ρVx	g =ρS(l − x)g ,		(4.1)
	где	M x	и Vx -	масса и объем нижней
	части стержня.							x
	Пренебрегая			малым	изменением		l
	сечения S, возникающим в соответствие							F
	с формулой Пуассона, из (4.1) находим
	напряжение на расстоянии x от точки
	подвеса:
				F =ρg(l − x)				Рис. 4.1
			σx =
				S

Удлинение стержня можно найти, используя дифференциальную форму закона Гука. Деформация равна относительному удлинению малого участка dx:

dudx = σEx = ρEg (l − x),

или

du = ρg (l − x)dx .	(4.2)
E
Очевидно, что деформация неоднородная.
Удлинение стержня δl равно величине u(x) при	x =l , значение u(x)

находим из (4.2) интегрированием с учетом граничного условия u(0) = 0:

	x				x	ρg
	u(x) = ∫ρg		(l − x)dx =	ρg ∫(l − x)dx =			(2xl − x2 ) ,
						2E
	0	E		E	0

17

откуда следует

δl =u(l) = ρgl2 . 2E

Полное относительное удлинение стержня:

ε = δll = 2ρEg l l .

Что будет происходить при увеличении длины стержня? Сила притяжения Земли (массовая сила) будет приводить к увеличению неоднородной

деформации подвешенного стержня. На участках, где деформация dudx

выше (вблизи точки подвеса) процессы разрушения начнутся в первую очередь. Можно ли так изменить форму, чтобы деформация стала

однородной? Чтобы выполнялось условие dudx = const , нужно, чтобы

напряжение было однородным по всей длине образца: σx = σ = const . Но сила меняется с изменением x, значит должно меняться и сечение стержня.

Найдем S(x), считая S(0) = S0. Сила в сечении S(x) определяется весом нижней части стержня:

Fx =ρVx g ,

где

Vx = ∫l S(x)dx .

x

Величина напряжения описывается выражением

		F		ρg	l
	σ =	x	=		∫S(x)dx ,
		S(x)		S(x)
					x

откуда следует

σS(x) =ρg∫l S(x)dx .

x

Дифференцируя обе части этого уравнения по x, находим:

18

S′(x) = −ρσg S(x).

Решением данного уравнения является экспоненциальная функция. С учетом начального условия S(0)=S0 получаем:

S(x) = S0 exp(−ρσg x) .

Для получения однородной деформации тело должно экспоненциально

сужаться в направлении вниз от закрепленного конца. Поскольку

напряжение не зависит от x, полная деформация будет описываться выражением δll = Eσ , как и в случае растяжения однородного стержня.

Лекция 3

4.2.Деформация кручения

4.2.1. Кручение тонкостенного цилиндра

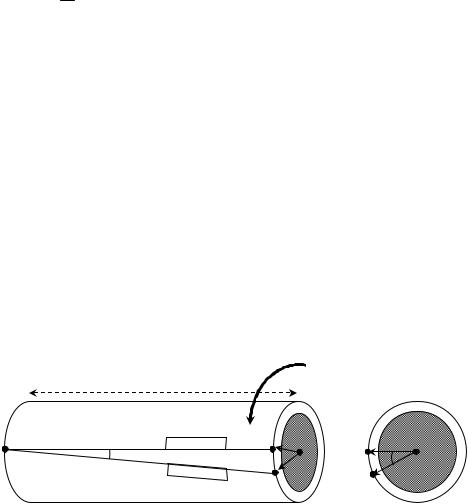
Рассмотрим тонкостенный цилиндр длиной L, радиуса r и толщиной dr. Закрепим один из его концов, а к другому приложим крутящий момент M, как показано на рисунке 4.5. Сдвиговое напряжение g, создающее

крутильный момент и приложенное к свободному торцу цилиндра, будем

считать постоянным. Образующая AB цилиндра после деформации кручения отклонится на малый угол ϑ, а радиус-вектор, направленный от оси цилиндра в точку B, повернется на угол ϕ (см. рис 4.5).

	L	M
ϑ	K	B r	B	r
A				ϕ
	K'	B'	B'

Рис. 4.5

Угол ϑ можно выразить через длину дуги BB' и длину цилиндра L:

19
ϑ=	BB′			,
		L
где
BB′ = rϕ,
откуда
ϑ=		r	ϕ.		(4.3)
		L

Найдем связь между крутильным моментом M, углом поворота ϕ цилиндра и упругими свойствами материала. Выделим на поверхности цилиндра малый элемент K, имеющий форму параллелепипеда (рис. 4.5). В результате деформации кручения выбранный нами элемент сместится и испытает перекос (рис. 4.6), который можно рассматривать как

деформацию сдвига. Применяя формулы, полученные для описания

деформации сдвига, находим:

ϑ= µg .

Учитывая соотношение (4.3), получаем							До деформации кручения
	g		r					K
		=		ϕ,
µ			L					ϑ
откуда следует
				µr
								K'
		g = L ϕ.			(4.4)
						После деформации кручения
Эту зависимость мы нашли, используя							Рис. 4.6
формулы для деформации однородного

сдвига.

Свяжем величину поверхностного напряжения g c крутильным моментом

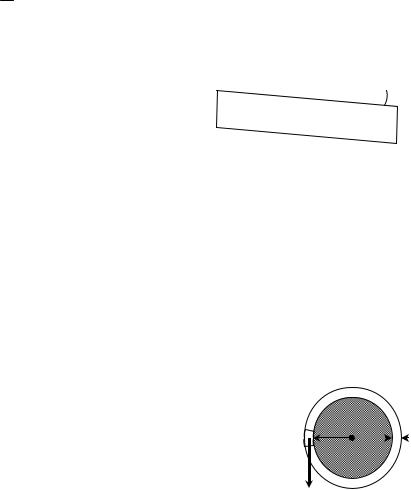
M. Из рисунка 4.7 находим

dM = dG r ,

где dG = gdl dr , откуда получаем

dM = grdl dr .	dl	r	dr
Интегрируя по длине окружности радиуса r,	dG
приходим к соотношению
		Рис. 4.7

20

2πr

M = grdr ∫dl = 2πr2 gdr .

0

Используя формулу (4.4), находим

M = 2πr3µϕdr .

L

Это выражение позволяет вычислить зависимость M от ϕ для

толстостенной трубки и для сплошного цилиндра.

4.2.2. Толстостенная трубка

Рассмотрим толстостенную трубку с внутренним радиусом r1 и внешним радиусом r2. Представим, что эта трубка является набором тонкостенных трубок толщиной dx, тогда момент сил находится интегрированием:

	r	2πµϕ					2πµϕ	r
	M = ∫2			r3dr =				∫2		r3dr .
	r		L				L		r
	1								1
	Поскольку	r2
			r3dr		1(r4		− r4 ),
		∫		=
					4	2	1
		r1

для момента сил получаем

M = fϕ,

где f = πµ2L (r24 − r14 ) - крутильная жесткость трубки.

4.2.3. Сплошной цилиндр

Сплошной цилиндр радиуса R можно рассматривать как частный случай толстостенной трубки при r1 = 0 и r2 = R, откуда следует

	M = fϕ; f =	πµR4	.
		2L

Отметим, что жесткость стержня пропорциональна µR4 и обратно пропорциональна его длине L.

4.2.4. Кручение как неоднородная деформация

Мысленно выделим в стержне две тонкие трубки радиусами r1 < r2 . Поскольку для соответствующих углов справедливы соотношения