[ Филиппов ] Теория упругости (лекции)

21

ϑ1 = rL1 ϕ ; ϑ2 = rL2 ϕ,

величины этих углов удовлетворяют условию ϑ2 > ϑ1. Отсюда следует, что

при кручении внутренние слои испытывают меньшую деформацию, чем внешние, т.е. деформация является неоднородной.

4.2.5. Изменение объема тела при кручении

Как было показано в начале раздела 4.2, деформация кручения в тонком слое может быть представлена как деформация сдвига, следовательно, объем тонкого слоя, а значит и всего тела, при деформации кручения не меняется.

4.2.6. Крутильные весы

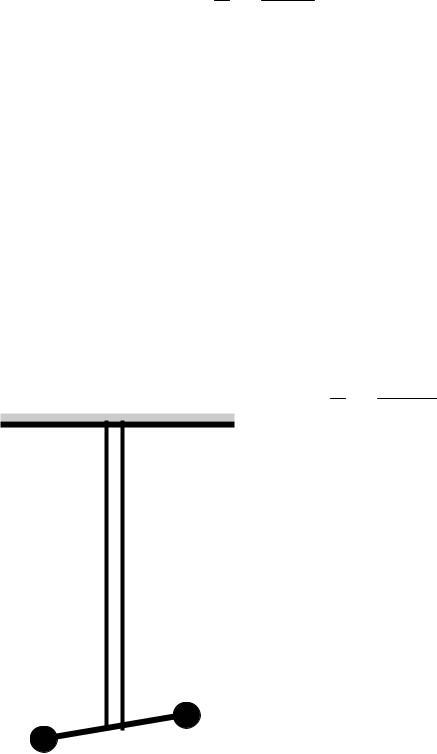
Оценим величину крутильной жесткости цилиндра. Возьмем стержень длиной 1 м, закрепим его одним концом, и будем создавать момент сил на другом конце, прикладывая силы к перекладине длиной 0,1 м. (Рис. 4.8). Момент сил при этом равен

M = 2F

l

= F l .

2

Какой момент нужен, чтобы

повернуть стержень на угол 10?

Радианная мера такого угла равна

ϕ =

2π

≈ 0,02 .

L

360

Для поворота на угол ϕ нужно

приложить

силу

F =

f

ϕ.

Рассчитаем величину f

l

для стали:

F

Е = 2 1011 Н/м2; ν = 0,26;

µ ≈ 0,8 1011 Н/м2. Расчет проведем

в трех вариантах, отличающихся

l

F

толщиной стержня R.

Вариант 1.

Рис. 4.8

R = 0,01 м.

f =

πµR4

=

π0,8 1011 10−8 ≈1,3 103 Нм;

2L

2 1

22

F = lf ϕ =1,30,101 3 0,02 ≈300Н .

Вариант 2.

R= 0,001 м (проволока).

f =	πµR4		= π0,8 1011 10−12				≈1,3 10−1	Нм;
	2L				2 1
	F =		f	ϕ =	1,3 10−1	0,02 ≈ 0,03Н .
			l		0,1

Вариант 3.

R = 0,0001 м (стальная нить).

f =	πµR4	=	π0,8 1011 10−16	≈1,3 10−5 Н м;
	2L		2 1

F = lf ϕ =1,3010,1 −5 0,02 ≈3 10−6 Н .

Стальную нить можно использовать в качестве крутильного динамометра (крутильных весов). С его помощью можем измерять силы в 10-5 - 10-6 Н. Кулон открыл свой закон, исследуя силы

Lпритяжения и отталкивания заряженных шариков с помощью крутильных весов.

4.2.6. Крутильный маятник

Прикрепим

к

концам

невесомой

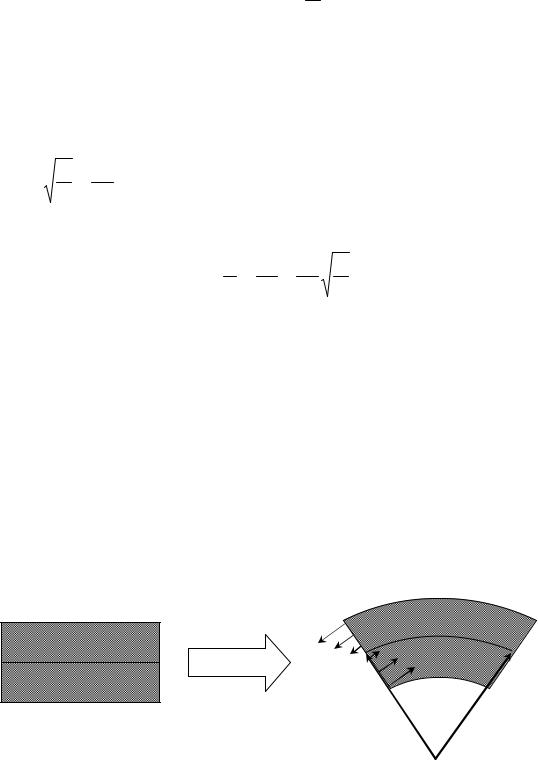
перекладины (Рис. 4.9) маленькие шарики

m

весом по m = 10-3 кг.

Момент инерции

m

шариков

относительно

центра

l

перекладины

будет

описываться

выражением

Рис. 4.9

l

2

1

2

I

= 2m

=

2

ml

,

2

откуда получаем I = 0,5 10−5

кг·м2.

23

Выведем систему из равновесия, повернув на угол φ0. Возникнет момент сил, стремящийся вернуть систему в положение равновесия. При этом угловое ускорение будет описываться формулой

ϕ&& = − MI = − If ϕ,

представляющей собой уравнение гармонических колебаний. Его решением будет функция

ϕ = ϕ0 cos(ωt +α) ,

где ω=	f	=	2π	- циклическая	частота,		Т – период колебаний, α -
	I		T
начальная фаза колебаний. Частота колебаний в Герцах будет равна
				ν = 1 =	ω =	1	f .
				T	2π	2π	I

Для проволоки R = 1мм с крутильной жесткостью f = 0,13 Н·м находим ν ≈ 25 Гц. Частота зависит не от массы, а от момента инерции: если уменьшим массу, но соответствующим образом увеличим l, частота останется неизменной в отличие от случая пружинного маятника.

4.3Деформация изгиба

4.3.1. Изгиб балки

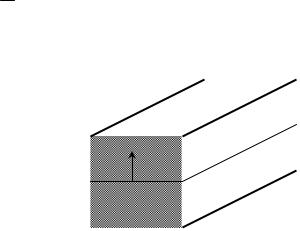
Исследуем закономерности деформации изгиба на примере балки, длина которой значительно превосходит ее поперечные размеры. Рассмотрим изгиб малого элемента балки (Рис. 4.10), выделив в нем нейтральную

l+dl

σ 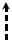y

Изгиб	l
l

ϑ R

Рис. 4.10

24

поверхность, не испытывающую деформации растяжения-сжатия. Будем рассчитывать величину y от этой поверхности. Над этой поверхностью балка будет испытывать деформацию растяжения, а ниже нейтральной поверхности - деформацию сжатия. Благодаря этому, в каждом сечении изогнутой балки возникает момент сил.

Найдем величину деформации слоя, смещенного на расстояние y от

	нейтрального слоя. Из анализа	рисунка 4.10			следует l = ϑR и
	l + δl = ϑ(R + y) , откуда получаем	ϑ=	l	и δl = ϑy =	l	y . Из последнего
			R		R

выражения находим формулу для деформации смещенного слоя:

δll = Ry .

Согласно закону Гука, напряжение в этом слое будет равно следующей величине:

	σ( y) = E δl = E			y	.
	l			R
	Найдем момент сил, действующий на
									y
	сечение, ограничивающее слева выделенный
	фрагмент балки (Рис.	4.10). Сила dF ,
	действующая вдоль смещенного слоя равна
	dF = σdS = E	y	dS ,
		R
	а выражение для соответствующего момента								Рис. 4.11
	сил имеет вид:					y2
	dM = dFy = σydS = E							dS .
							R

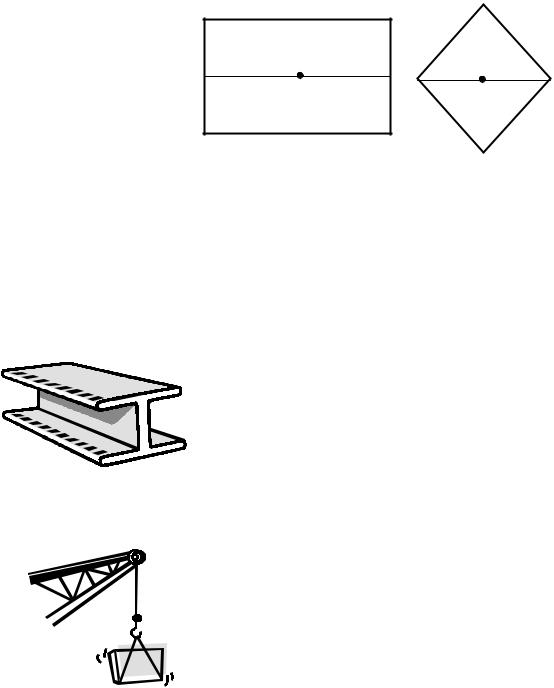
Проинтегрируем правую и левую части этого уравнения по всему сечению

(Рис. 4.11):

M =	E	∫y2dS .	(4.5)
	R	S

Величину I = ∫y2dS называют моментом инерции поперечного сечения

S

балки, относительно поперечной оси, лежащей в нейтральном сечении. Используя это обозначение, уравнение (4.5) можно переписать в виде

M =	E	I .	(4.6)
	R

25

Это	уравнение является
основным в теории изгиба
балок.
При чистом изгибе, когда			C
сумма сил, действующих в
поперечном сечении, равна
нулю (средняя продольная
деформация		растяжения-
сжатия отсутствует), линия
y=0	проходит	через центр тяжести C
(Рис. 4.12).

C

Рис. 4.12

поперечного сечения балки

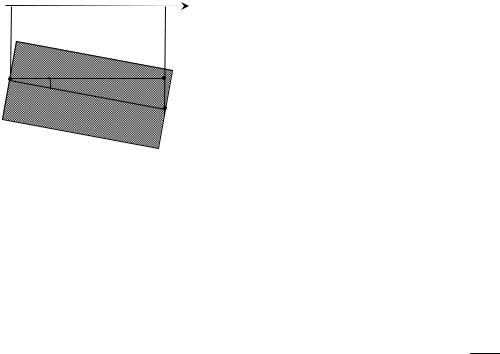
4.3.2. Жесткость балки

Согласно уравнению (4.6),

Рис. 4.13

Рис. 4.14

момент сил M пропорционален моменту инерции поперечного сечения I. Для увеличения жесткости балок им придают специальную профильную форму (Рис. 4.13), увеличивающую величину I при изгибе в определенном направлении. В технике также часто используют так называемые фермы (Рис. 4.14), обладающие большим моментом I при малом расходе материала и весе.

Рассчитаем момент инерции сечений для простейших случаев.

Круглое сечение радиуса R.

dS = rdrdα; y = r sin α;

	2π	R	πR4		S 2
	I = ∫sin2 α dα∫r3dr =			=		;
			4		4π
	0	0

.

Прямоугольник со сторонами a и b.

dS = dxdy ; S = 4ab ;

26

2b	a	2	dy =	4	3	a S 2	.
I = ∫dx ∫y				3	a b =	b 12
0	−a

Лекция 4

4.3.3. Прогиб консольной балки

Рассмотрим малый прогиб консольной балки (балки, один из концов которой жестко закреплен) под действием внешней силы, приложенной к свободному концу балки (Рис. 4.15). Саму балку будем считать невесомой.

z	x
dx
	F

Рис. 4.15

Найдем величину смещения z(x) балки от горизонтального положения под действием приложенной силы. Момент сил на расстоянии x от точки крепления описывается выражением:

		M = (l − x)F =						EI
dx	x								.	(4.7)
							R(x)
		Для того, чтобы найти радиус
		кривизны R(x) , рассмотрим малый
		фрагмент	балки,			схематически
		изображенный на				рисунке				4.16.
		Используя		условия					малости
R		прогиба, можно записать
			dϕ = dl			≈ dx		,
				R		R
Рис. 4.16		откуда получаем соотношение
			1			dϕ
					≈ dx ,
				R(x)

27
приводящее формулу (4.7) к виду:
M = EI	dϕ	.	(4.8)
	dx

Из рисунка 4.17 видно, что угол ϕ (поворот сечения) может быть выражен через производную функции z(x):

dxdz =tgϕ ≈ ϕ,

откуда следует

dϕ

≈

d 2 z

,

dx

dx2

что с учетом (4.7) и (4.8) дает

dx

x

M

= EI

d

2

z

= (l − x)F .

(4.9)

z

dx2

dx

Решая

это

уравнение

с граничными

dz

условиями

dl

z(0) = 0;

Рис. 4.17

dz

x=0

≈ ϕ

x=0

= 0 ,

dx

находим

F

x2

x3

z(x)=

(l

−

) .

EI

2

6

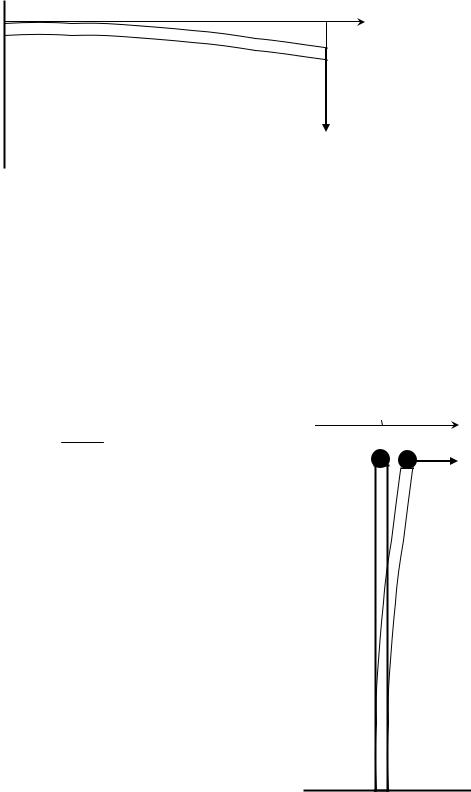
Найденная формула позволяет легко найти величину z(l) = Fl3 - стрелу

3EI

прогиба консольной балки (Рис. 4.18).

28

l	x
	z(l)

F

Рис. 4.18

4.3.4. Колебания нагруженной балки

Пусть на невесомую балку с закрепленным на конце точечным грузом массы m действует внешняя сила Fвн (Рис. 4.19). Действие этой силы

приводит к изгибу балки со значением стрелы прогиба

z = F3внEIl3 ,

откуда следует

= 3EI

Fвн l3 Z .

Со стороны балки при этом на груз действует сила

F = −F = −

3EI

z ..

(4.10)

вн l3

Если убрать внешнюю силу, груз начнет двигаться с ускорением, определяемым формулой

F = m ∂2Z ,

∂t2

0 z

Fвн

Рис. 4.19

29

откуда с учетом (4.10) получаем:

	∂2 z	= −	3EI	z .
	∂t2		ml3

Решением этого уравнения является гармоническая функция

z(t) = z0 cos(ωt +α) ,
описывающая процесс колебаний с частотой ω=	3EI .
	ml3

4.3.5. Перерезывающая сила

Рассмотрим малый элемент балки dx, испытывающей слабую деформацию изгиба (Рис. 4.20). Условие равенства нулю суммы моментов сил относительно точки А

M (x) − M (x + dx) − Fпdx = 0

можно переписать в виде

			dM (x) dx + F dx = 0 ,
			dx	п
откуда		следует		dx
выражение	для	силы,
компенсирующей			M(x)
отличную	от	нуля
			А		-M(x+dx)
разность моментов сил в
сечениях x и x + dx:
F = −dM (x) .
п	dx				Fn
Эта сила	называется			Рис. 4.20
перерезывающей,		ее

наличие свидетельствует о появлении при изгибе консольной балки не только деформаций растяжения-сжатия, но и слабых сдвиговых

деформаций. Поскольку M (x) = REI(x) , то сдвиговые деформации появляются при изгибах с переменным радиусом кривизны R(x).

30

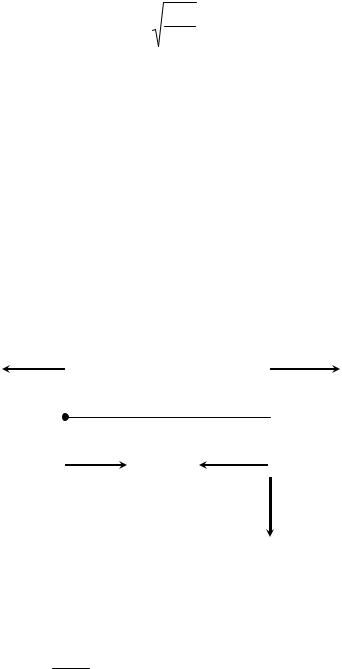
4.3.6. Устойчивость упругого равновесия
Рассмотрим	упругие	деформации	стержня,			F
закрепленного вертикально. Если на стержень
действует растягивающая сила (Рис. 4.21), то
при малых отклонениях от вертикали он
достаточно быстро вернется в исходное
положение. Для деформации сжатия (Рис. 4.22)
существует	некая	критическая	величина
внешней силы Fкр.		При F < Fкр –	быстрое
возвращение в вертикальное состояние. При
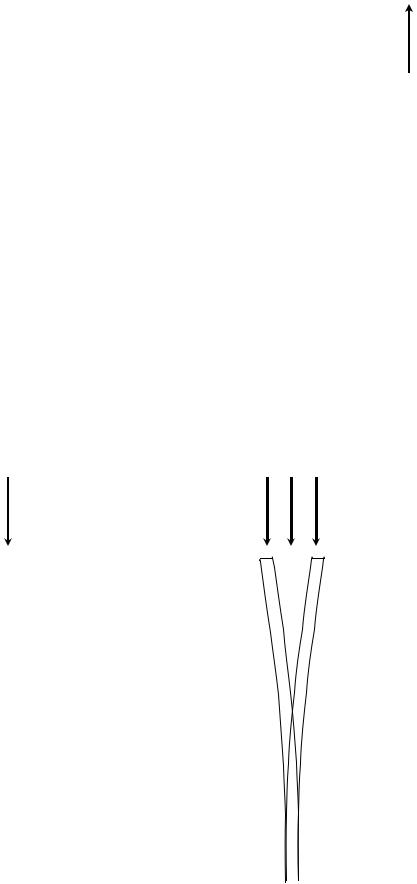
F = Fкр имеет	место	бифуркация -	два (или
более) устойчивых положения (Рис. 4.23). При
F > Fкр – устойчивой является криволинейная
форма, однако изгибы и напряжения очень
велики, что часто ведет к разрушению.

Рис. 4.21

		F < Fкр				F = Fкр

Рис. 4.22

Рис. 4.23