
[ Филиппов ] Теория упругости (лекции)
.pdf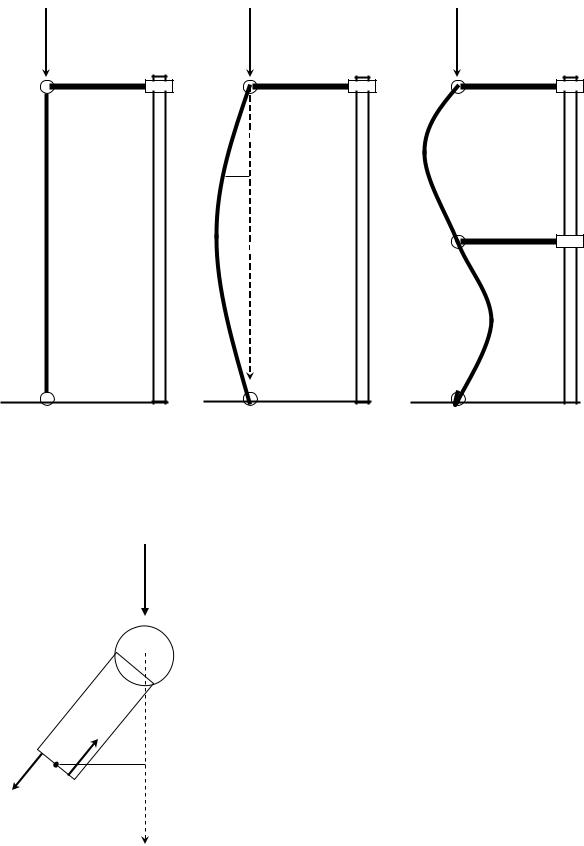
31
F < Fкр |
|
F = Fкр |
|
F = F2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
z
x
Рис. 4.25 |
Рис. 4.27 |
Рис. 4.28 |
Задача об устойчивости стержня в XVIII в. была решена Эйлером. Рассчитаем значение критической силы и форму стержня, закрепленного
шарнирно за оба конца (Рис. 4.25).
А
M(x)
FРассмотрим условие равновесия участка стержня от x = 0 до x (Рис. 4.26). В сечении x
возникает момент сил Mx. Из уравнения (4.9) с учетом изменившегося направления оси x следует:
|
M x = −EI |
d 2 z |
. |
(4.11) |
|
dx2 |
|||
|
|
|
|
|
z(x) |
Сумма момента Mx и момента сдавливающей |
|||
|
силы -Fz(x) должна быть равна нулю: |
|
||
x |
M x − Fz(x) = 0, |
|
||
Рис. 4.26 откуда, учитывая (4.11), находим

32
d 2 z = − F z(x). dx2 EI
Решение этого уравнения можно записать в следующем виде:
z(x)= Acos kx + Bsin kx ,
где |
F . |
|
k = |
(4.12) |
|
|
EI |
|
Из граничного условия z(0) = 0 получаем
z(x)= Bsin kx .
Учитывая второе граничное условие z(l)=0, находим kl = nπ, откуда с учетом (4.12) следует
Fn = EI π2 n2 . l2
Минимальное значение силы достигается при n = 1:
F1 = EI π2 . l2
Это и есть искомое значение критической силы. При F < F1 = Fкр стержень остается прямолинейным. При F = Fкр равновесными будут состояния с любым прогибом и любым значением амплитуды B (Рис. 4.28). Реально, при больших значениях B деформации перестают быть малыми, и требуется более строгая теория. Эта более строгая теория и дает конкретную формулу при F > Fкр.
Состояния n = 2,3,… являются неустойчивыми. Их можно наблюдать, например, если дополнительно закрепить стержень шарнирной опорой в средней точке (Рис. 4.28). Для такого крепления: Fкр = F2 = 4F1.
33
5.ВОЛНОВЫЕ ЯВЛЕНИЯ В УПРУГИХ СРЕДАХ
5.1.Продольные волны в стержне
5.1.1. Волновое уравнение
Рассмотрим однородный стержень бесконечной длины. Плотность материала стержня ρ, модуль Юнга E, сечение S. После удара в торец стержня, вдоль него побежит волна упругой деформации. Смещение u в любой точке будет зависеть от времени:
x(t) = x +U (x,t)
По закону Гука на сечение x действует сила:
F(x,t) = ES |
∂u(x,t) |
, |
(5.1) |
|
∂x |
|
|
|
|
|
x |
|
|
|
|
|
F(x-∆x/2) |
|
F(x+∆x/2) |
||
|
|
|
|
|
Рис. 5.1
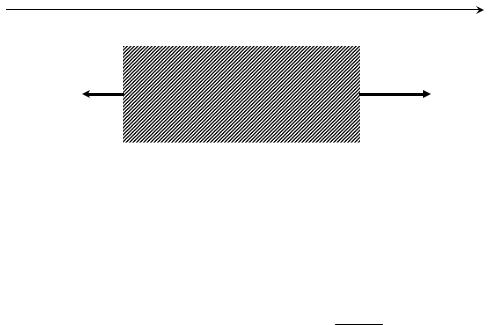
Выражение для суммарной силы, действующей на выделенный элемент бруска (Рис. 5.1) с объемом ∆V = S∆x и массой ∆m =ρ∆V =ρS∆x , может быть записано в виде:
∆F = F(x + ∆2x) − F(x − ∆2x) ≈ ∂F∂(xx) ∆x ,
или, с учетом (5.1),
∆F = |
∂2u(x,t) |
SE∆x . |
|
∂x2 |
|||
|
|
При отличной от нуля силе ∆F выделенный элемент бруска будет двигаться с ускорением:
34
= ∂2u(x,t) ax ∂t2
Согласно второму закону Ньютона: ∆max = ∆F , или
ρS∆x ∂2u = SE∆x ∂2u .
∂t2 ∂x2
После сокращения подобных членов это уравнение приводится к виду:
u(x) |
f |
|
|
|
∂2u |
= c2 ∂2u |
, |
|
||
|
|
|
|
∂t2 |
1 |
∂x2 |
|
|
||
|
|
|
|
представляющему |
собой |
|||||
|
|
c1 |
|
уравнение волнового движения, |
||||||
|
|
|
|
где |
c = |
E |
- |
скорость |
||
|
|
|
|
|
1 |
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
движения |
|
волны. |
Решение |
|||
|
|
|
|
этого |
уравнения может |
быть |
||||
|
|
|
|
записано в виде суммы двух |
||||||
0 |
20 |
40 |
60 |
членов: |
|
|
|
|
|
|
80 |
|
|
|
|
|
|
||||
|
|
x |
|
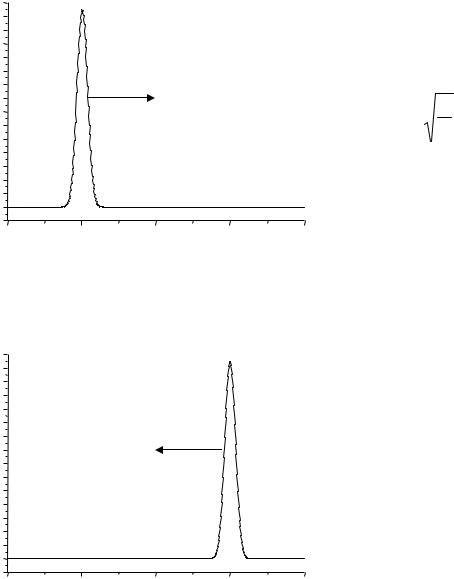
u(x,t) = f (x −c1t) + g(x + c1t), |
||||||
|
|
|
|
|||||||
|
|
Рис. 5.2 |
|
где f |
и |
g |
– |
произвольные |
||
|
|
|
|
|||||||
u(x) |
|
|
|
функции. Волна возмущения f |
||||||
|
|
g |
распространяется |
|
|
без |
||||
|
|
|
|
|
||||||
|
|
|
изменения |
своей |
формы |
по |
||||
|
|
|
|
направлению оси x (Рис. 5.1), а |
||||||
|
|
c1 |
|
волна |
g - |
в противоположном |
||||
|
|
|
(Рис. 5.2) направлении (прямая |
|||||||
|
|
|
|
|||||||
волна и обратная волна).
0 |
20 |
40 |
60 |
80 |
x
Рис. 5.3

35
Лекция 5
5.1.2. Звуковые волны в тонком стержне
Рассмотрим характеристики звуковой волны, распространяющейся в бесконечном упругом стержне. Для определенности будем говорить о звуковой волне определенного тона (частоты):
u(x,t) = B cos(kx −ωt + ϕ0 ) ,
такие волны называются гармоническими. Аргумент гармонической функции ϕ = kx −ωt + ϕ0 называется фазой волны,
ϕ0 - начальная фаза;
ω= 2Tπ - циклическая частота;
T- период колебаний волны; k = 2λπ - волновое число;
λ - длина волны.
Очевидно, что ωk = Tλ = c1 - скорость распространения волны.
При выводе основных формул распространения волн в стержне, мы рассматривали стержень бесконечной длины, который, формально говоря, всегда можно считать тонким (длина гораздо больше толщины). С физической точки зрения, в распространяющейся вдоль стержня волне есть характерный линейный параметр - длина волны, поэтому выведенные в предыдущем разделе формулы оказываются справедливыми не для всякого стержня. Необходимо, чтобы стержень является тонким на отрезке длиной λ, т.е. для поперечных размеров стержня H должно выполняться условие:
H << λ.
Оценим длину волны звуковых колебаний для стального стержня. Величина λ = c1 T определяется скоростью распространения волны,
постоянной для данного вещества, и периодом ее колебаний. Для стали
11 |
Н |
|
3 кг |
|
|
E = 2 10 |
|
, ρ =8 10 |
м3 , откуда следует |
|
|
м2 |
|
||||
|
|
c = |
2 1011 |
= 0,5 104 =5000 м =5 км , |
|
|
|
1 |
8 103 |
с |
с |
|
|
|
|||
36
что более чем в 10 раз превышает скорость звука в воздухе cg ≈ 0,3 кмс .
Частота ν = |
1 |
для звуковых волн лежит в диапазоне от 20 Гц до 20 кГц. |
|
T |
|||
|
|
Возьмем для оценок ν =50 кГц, что соответствует частоте ультразвуковых колебаний, тогда
λ = |
c |
= |
5 103 |
= 0,1м. |
|
1 |
|
||||
50 103 |
|||||
|
ν |
|
|
Очевидно, колебания звукового диапазона будут обладать еще большими длинами волн. Значит, стальной стержень диаметром 1 см уже можно считать тонким для задач по прохождению звуковых волн.
5.2.Волны в тонких пластинках
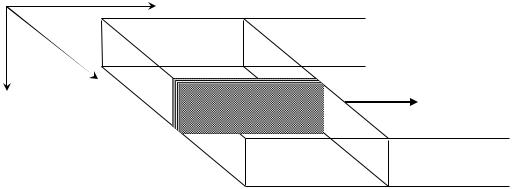
Рассмотрим тонкую, широкую и длинную пластину из однородного материала с плотностью ρ и модулем Юнга E (рис. 5.4).
x
z y
∆y
Рис. 5.4
Предположим, что вдоль оси x в пластине со скоростью c2
распространяется возмущение продольного растяжения-сжатия (смещения u(x,t) происходят вдоль оси x и не зависят от y и z). Для анализа этого процесса выделим в направлении x узкий фрагмент пластины, «брусочек», шириной ∆y (рис. 5.4). На рисунке 5.5 изображен вид сверху (в направлении оси z) на пластину с выделенным фрагментом. По обе стороны от этого фрагмента выделим еще по такому же узкому бруску. Если в области ∆x эти бруски испытывают деформацию сжатия в направлении x, то по закону Пуассона они увеличивают свои размеры в
37
направлении z. Но в направлении y они друг другу «мешают», т.к. каждый из соседей хочет увеличить свои размеры, и на границу раздела этих брусков начинают действовать противоположные по направлению, но равные по величине силы.
x
∆x
∆y ∆y ∆y
y
Рис. 5.5
Эти силы уравновешивают друг друга и препятствуют изменению размеров брусков в направлении y. Мы имеем задачу о продольных волнах
встержне с запрещенными боковыми смещениями, которую уже решали.
Втаком стержне продольные упругие деформации по-прежнему подчиняется закону Гука
F |
= E |
|
∂u , |
|
||||
S |
|
|
эф ∂x |
|
||||
но с эффективным модулем Юнга E |
эф |
= |
|
|
E |
. |
||
1 |
−ν2 |
|||||||
|
|
|
|
|||||
Применяя к нашему бруску те же рассуждения, что и к свободному |
||
стержню в разделе 5.1, получим для деформации u(x,t) |
следующее |
|
волновое уравнение |
|
|
∂2u |
= c2 ∂2u |
|
∂t2 |
2 ∂x2 |
|
|
38 |
где |
|
c |
= Eэф . |
2 |
ρ |
|
Прием, который мы применили, рассматривая тонкие пластины, можно использовать и для анализа распространения волны в неограниченных средах.
5.3.Волны в неограниченных упругих средах
5.3.1. Продольные волны
Рассмотрим волны, связанные с деформациями растяжения-сдвига в неограниченных упругих средах, причем направление этих деформаций совпадает с направлением распространения волны. Такие волны
x
z
y
Рис. 5.6
называются продольными. Пусть волна распространяется в направлении x, и величина смещения u(x,t) не зависит от y и z. Выделим тонкий брусок с малыми размерами ∆y,∆z, вытянутый в направлении x (рис. 5.6). Рассуждениями, аналогичными приведенным в предыдущем разделе, можно показать, что при продольных деформациях растяжения-сжатия в направлении x поперечные деформации в направлении y и z будут запрещены. Мы имеем задачу о продольных деформациях в стержне с полностью запрещенными боковыми смещениями. Полученное нами ранее решение показывает, что закон Гука для продольных деформаций выполняется:
39
FS = Eэф′ ∂∂Ux ,
но значение эффективного модуля Юнга оказывается другим:
′ |
|
E(1−ν) |
. |
|
|
||
Eэф = |
(1 |
+ ν)(1− 2ν) |
|
|
|
В соответствии с этим, скорость распространения плоской волны в
неограниченном упругом теле: c |
′ |
= Eэф |
|
3 |
ρ |
|
|
x |
|
x)
z
y
Рис. 5.7
5.3.2. Поперечные волны
Кроме деформаций растяжения-сжатия, в упругом теле возможны и деформации другого типа - сдвиговые. Пусть два соседних слоя (yz) в непрерывной среде, отстоящие друг от друга на величину ∆x испытывают сдвиг относительно друг друга в направлении z (рис. 5.7). Такое упругое возмущение будет распространяться как плоская волна в направлении оси x. Скорость распространения такой волны, как можно показать, будет
равна c = |
µ |
, где µ – модуль сдвига. Такие волны, при которых смещения |
|
ρ |
|
точек среды перпендикулярны направлению распространения волны, называют поперечными или сдвиговыми. Если в случае продольных волн

40
достаточно было указать направление распространения волны, то поперечная волна только лишь своим направлением охарактеризована быть не может. Существенным будет еще и направление, в котором происходят сдвиговые деформации. При движении вдоль оси x, сдвиговые деформации могут происходить вдоль z или y, эти направления называются направлениями поляризации волны. Дополнительная характеристика – поляризация, есть неотъемлемое свойство поперечных волн. Поляризацию поперечной механической волны можно измерить (определить) различными экспериментальными методами. Световые волны при первых попытках их теоретического описания, тоже пришлось отнести к поперечным, поскольку была обнаружена их поляризация. Продольные волны поляризацией не обладают.
5.4Скорости распространения упругих волн
Сравним скорости распространения упругих волн в изученных случаях:
Продольные:
Стержень |
c = E |
; E |
|
|
1 |
ρ |
|
|
|
|
|
Пластина |
c2 |
= |
Неограниченная среда |
c3 |
= |
Поперечные: |
|
|
Неограниченная среда |
c = |
|
Поскольку µ < E < Eэф < Eэф′ , то
Eэф ;
 ρ
ρ
Eэф′ ;
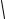 ρ
ρ
 µρ ; c < c1
µρ ; c < c1
Eэф =1−Eν2
′ |
|
E(1−ν) |
|
|
|
Eэф = |
(1 |
+ ν)(1− 2ν) |
|
µ = 2(1E+ ν)
< c2 < c3 .
5.5.Крутильные волны в стержнях
Рассмотрим малый (длиной ∆x) фрагмент стержня радиуса R, испытывающего крутильные возмущения. Угол поворота данного фрагмента (деформация кручения) может быть описан выражением:
∆ϕ = ϕ(x) −ϕ(x − ∆x) ≈ ∂∂ϕx ∆x .
Действующий в сечении x момент сил, соответствующий этой деформации, есть
