[ Филиппов ] Гидродинамика (лекции)

11

ρ ∂∂t + v v = −grad(P ) .

Это уравнение нелинейно по v , его решение может быть выполнено только приближенными численными методами. Поэтому в основном мы будем рассматривать простые случаи, в частности, одномерные потоки жидкости.

2.СЖИМАЕМАЯ ЖИДКОСТЬ

2.1.Уравнение непрерывности для сжимаемой жидкости

Рассмотрим поток массы газа или жидкости через площадку dS , расположенную нормально к потоку.

dNM =ρvdS

- масса, протекающая в единицу времени через данную площадку.

Рассмотрим параллелепипед объемом dxdydz . Обозначим

R(x,y,z )=ρ(x,y,z )v(x,y,z ).

Поток через параллелепипед:

dM =[R(x +dx)−R(x)]dydz +[R(y +dy)−R(y)]dxdz

+[R(z +dz )−R(z )]dxdy =

	∂R		∂R		∂R
		+		+
=	∂x		∂y		∂z	dxdydz =

=div(ρv)dxdydz .

Нестационарный поток может привести к изменению массы внутри выбранного объема на величину

dM = −div(ρv)dxdydz

с учетом того, что при положительной величине потока через некоторый объем масса внутри этого объема убывает. С другой стороны, это изменение массы может быть описано выражением

12

dM = ∂∂ρt dxdydz .

Приравнивая эти изменения массы, получаем:

∂∂ρt dxdydz +div(ρv)dxdydz = 0 ,

или

∂∂ρt +div(ρv)= 0

- уравнение непрерывности для сжимаемой жидкости.

2.2. Уравнение Эйлера для сжимаемой жидкости

Уравнение Эйлера для несжимаемой жидкости является, по сути, формой записи второго закона Ньютона применительно к сплошным средам:

ρddvt = −gradP .

Это уравнение содержит значение ρв конкретной точке и не меняет своего вида в случае, когда ρстановится функцией координат. Это уравнение должно быть дополнено уравнением непрерывности. Но и это недостаточно, т.к. теперь у нас от координат и времени зависят уже пять величин: vx , vy , vz , P и ρ. Необходимо еще одно уравнение. Это

уравнение называют материальное уравнение, оно описывает связь между плотностью и давлением среды:

P =P (ρ).

2.3.Звуковые волны

2.3.1. Волновое уравнение

Рассмотрим уравнение Эйлера, переписав его в виде:

∂∂vt +(v )v − ρp = 0 .

13

Рассмотрим распространение звуковых волн малой амплитуды в неподвижной среде. Будем считать, что в результате внешних возмущений

частица	жидкости		приобретают скорость v , а					значения	плотности и
давления	начинают				отличаться	от	средних	значений:	ρ =ρ0 +ρ′;
P =P0 +P′.		Будем	в	соответствие		с	нашим подходом считать малыми
величинами		′	P	′	и оставим в уравнениях только линейные по этим
		v , ρ ,

величинам члены.

1)Уравнение Эйлера:

∂v	+ (v )v −	P	≈	∂v	+	(P0 + P ′)	=	∂v	+	P ′	= 0
∂t		ρ		∂t		′		∂t		ρ0
						ρ0 + ρ

т.к.

P0 = 0 ;

2)Уравнение непрерывности:

∂(ρ0∂t+ ρ′)+ [(ρ0 + ρ′)v]≈ ∂∂ρt′ + ρ0 v = 0 ;

3)Уравнение P =P(ρ) представим в виде:

dPdt = ∂∂Pρ ddtρ .

Величина ∂∂Pρ зависит от конкретной среды и условий, в которых

происходит	изменения ρи P. При распространении звуковых		волн
изменения ρи P		происходят так быстро, что связанные с этим изменения
температуры	не	успевают приводить к процессам теплообмена,	т.е.

процесс изменения давления - адиабатический и ∂∂Pρ надо рассматривать для случая адиабатики. При увеличении ρувеличивается p ; ∂∂Pρ > 0 .

Обозначим: c 2 = ∂∂Pρ

14

dPdt =c 2 ddtρ ;

∂P′	+(v )(P0	+P′)=c 2	∂ρ′	+(v )(ρ0	+ρ′)	;
∂t
		∂t

ρ0 − P0 = 0 ;

∂∂Pt′ =c 2 ∂∂ρt′ .

Итак, имеем (опуская для простоты знак "штрих"),

∂∂ρt +ρ0 v = 0 ;

∂v + P = 0 ; ∂t ρ0

∂∂Pt =c 2 ∂∂ρt ;

из (1) и (3) получаем:

12 ∂∂P +ρ0∆v = 0 . c t

Теперь продифференцируем это выражение по времени:

	1 ∂2P		+ρ0∆	∂v	= 0 .
	c 2	∂t2		∂t

С учетом (2)

	1 ∂2P		−ρ0	P	= 0 ,
	c 2	∂t2		ρ0

или

(1)

(2)

(3)

15

1 ∂2P −∆P = 0 . c 2 ∂t2

Это - волновое уравнение для распространения звуковых волн малой амплитуды в однородной среде.

2.3.2. Плоская волна

Пусть у нас имеется плоская волна, распространяющаяся в направлении x, тогда, как и в случае с волнами в упругой среде:

	∂2P	−	1	∂2P	= 0,
	∂x2		c 2	∂t2

и функция

P (x,t)= f (x −ct)+g(x +ct )

будет решением этого уравнения. Переменная c, очевидно, является скоростю звука в среде. Для гармоничных волн:

P = Acos(kx −ωt),

где k = 2λπ , ω= 2Tπ и c = Tλ = ωk .

2.3.3. Скорость звука в газах

Отчего зависит скорость звука c = ∂∂Pρ . Можно легко получить эту зависимость для газа. Для адиабатических процессов P =ργconst , где

	γ = cP >1, c		P	и	c - теплоемкости газа при постоянном давлении и
		cV			V
постоянном объеме. Таким образом,
	∂P	=const + γργ−1			= γP
	∂t				ρ

и мы в результате получаем:

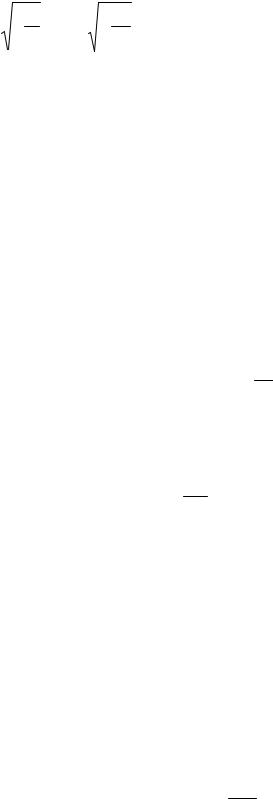
16

c =

γP ≈c =

γP0 .

Отметим, что скорость звука c

растет с ростом ρ0 ,

ρ

ρ0

но с ростом ρ0 растет и P0 , значит, c растет с ростом давления газа P0 .

Оценки:

кг

м

•

для атмосферного воздуха: γ ≈1,4 ; ρ =1,3

; P ≈105 Па; c ≈330

.

∂P

м3

с

•

для жидкостей

существенно больше.

Поэтому для воды

∂ρ

c ≈1200

м

.

с

2.3.4. Гармоническая волна

Рассмотрим, как изменяются скорости частиц при такого рода волнах. Воспользуемся уравнением:

∂v + 1 ∂P = 0 .

∂t ρ0 ∂x

Для гармоничной волны:

∂∂Px = −Ak sin(kx −ωt);

∂v = Ak sin(kx −ωt).

∂t ρ0

Поскольку среднее значение скорости равно нулю, получаем:

v = − Ak cos(kx −ωt),

ωρ0

или

v = − A cos(kx −ωt), cρ0

т.е. скорости частиц так же совершают колебательное движение, причем в противофазе с колебательным изменением давления.

17

2.4.Прохождение звука через границу раздела двух сред

2.4.1. Коэффициенты отражения и прохождения

Рассмотрим прохождение звука через границу раздела двух сред. Пусть две среды, отличающиеся плотностью (ρ1 и ρ2) и скоростями звука (с1 и с2) имеют плоскую границу раздела, перпендикулярную к x при x = x0 . Пусть

волна распространяется вдоль xв среде (1). На границе раздела раздела должно выполняться условие непрерывности. Без ограничения общности будем считать x0 = 0. В среде (1) будут распространяться две волны:

падающая на границу раздела

P1+ = Acos(k1x −ω1t);

v1+ = −ρA cos(k1x −ω1t)

1c1

и отраженная:

P1− =VA cos(−k1x −ω1t);

v1− = −ρA V cos(−k1x −ω1t),

1c1

где V - коэффициент отражения. В среде (2) распространяется одна волна, прошедшая через границу раздела:

P2 =WAcos(k2x −ω2t);

v	2	= −W	A	cos(k	x −ω t),
			2		2
			ρ2c2

где W - коэффициент прохождения. Условия непрерывности на границе при x = x0 = 0 :

P1+ +P1− =P2 и v1+ +v1− =v2 .

Конкретно с учетом x = 0 :

(1+V )Acos(ω1t)=WAcos(ω2t);

	18
(1−V )	A	cos(ω t)=W	A	cos(ω t)
	1		2
	ρ1c1		ρ2c2

Очевидно, это может выполняться только при ω1 = ω2 , т.е. частота

звуковой волны не меняется при прохождении границы раздела. Если так, то:

1+V =W ;

(1−V ) A =W A .

ρ1c1 ρ2c2

Решим это уравнение:

1+V = ρ2c2 (1−V );

ρ1c1

V= ρ2c2 −ρ1c1 ; ρ2c2 +ρ1c1

W =		2ρ2c2				.
	ρ c		2	+ρc
	2			1	1

Величину Z =ρc называют волновым сопротивлением или импедансом.

2.4.2. Граница вода-воздух

Рассмотри две ситуации, прохождение волны из более плотной среды в менее плотную и наоборот.

Z

ρ

c

10

3 кг

1200

возд

м

3

3

Например,

воды ≈

воды

≈

≈3 10

.

c

кг

330

Z

ρ

1,3

возд

возд

воды

м3

1) воздух-вода:

ρ1c1

<<1; V ≈1; W ≈ 2 .

ρ

c

2

2

P + +P

−

= A[cos(k x −ωt)+cos(−k x −ωt)]= 2Acos(k x)cos(ωt)

1

1

1

1

1

1

19

- стоячая волна с максимумом амплитуды при x = 0 .

							P2 = 2Acos(k2x −ωt)
- волна удвоенной амплитуды.
2) воздух-вода:			ρ1c1				>>1; V ≈ −1;	W ≈ 0.
			ρ	c	2
			2
P + +P − = A[cos(k x −ωt)−cos(−k x −ωt)]= 2Asin(k x)sin(ωt)
1	1					1		1	1	1

- стоячая волна с нулевой амплитудой вблизи границы раздела. Коэффициент прохождения через границу раздела - ноль.

Следствия:

•рыбы слышат нас, а мы их нет;

•тонкое стекло сильно заглушает звуки с улицы.

Вуравнениях идеальной жидкости мы не рассматривали силы вязкого трения. На самом деле они всегда присутствуют. Рассмотрим их влияние на течение жидкости, и условия, при которых их роль становится пренебрежимо мала.

3.ВЯЗКАЯ ЖИДКОСТЬ

3.1.Силы вязкого трения

Рассмотрим жидкость между двумя плоскими параллельными пластинами, площадью S . Верхняя пластина движется относительно нижней со

скоростью v. Если зазор h между пластинами мал: h << S , то опыт показывает:

F = ηS hv

Верхний слой жидкости движется вместе с пластиной со скоростью v, нижний покоится (v=0). В слое толщиной h при этом возникает сдвиговая сила трения F, пропорциональная S :

SF = ηhv ≈ ηdhdv .

20

Величина η - динамическая вязкость жидкости. Во многих задачах коэффициент вязкости входит в виде отношения ηρ. Величина ν = ηρ

называется кинематической вязкостью. Коэффициент вязкости зависит от температуры, причем при повышении температуры вязкость жидкости падает, а вязкость газов, как правило, слегка возрастает.

3.2.Уравнение Навье–Стокса

Для потока идеальной жидкости мы получили уравнение Эйлера:

ρddvt = −grad(P ) .

Если учесть силы вязкого трения, то вид этого уравнения изменится.

Сверху тонкого слоя:	F1′= ηdx1dx3		dv1		x2	+dx2
			dx2
	′	′′				d2v1	dx2
Снизу того же слоя:	∆F1 =F1	−F1 = ηdx1dx3 dx22

Сила, приложенная к единичному объему составляет:

			∆F				1			d2v
f		=	1	=					ηdx dx dx		1	;
					dx dx dx
	1		∆V					3	1 2	3 dx2
					1		2			2

f1 = ηd2v1 . dx22

Если мы учтем изменение скорости v1 вдоль направления x3, то получим:

f1	2	2
	= η d v21 + d v21		.
	dx2	dx3

Что будет, если скорость меняется и вдоль x1? Можно показать, что в этом случае для несжимаемой жидкости справедливо: