Березкин Основы теории информации и кодирования Лабораторный практикум 2009

5. Вывести аналитические выражения для p и q ДСКС, реализующего обнаруживающую и корректирующую способности.

6.Продумать последовательность действий при вычислении C двоичного канала, реализующего заданный циклический код (N, k).

7.Отразить подготовку в лабораторном отчете.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Используя обучающие и графические средства диалоговой программы, изучить принципы оценки информационной пропускной способности двоичных каналов.

2.Проверить расчеты, выполненные при подготовке, используя программную реализацию алгоритмов вычисления пропускной способности.

3. Исследовать ДК путем построения поверхности

C = F (p1 , p2 ) *.

4. Исследовать ДСКС путем построения поверхности

C= F ( p, q ) *.

5.Вычислить С ДСКС при реализации заданного циклического кода (N, k), обладающего только обнаруживающими способностями. Варианты приведены в табл. 6.1.

6.Вычислить C ДСКС при реализации заданного циклического кода (N, k), обладающего обнаруживающими и корректирующими способностями.

Таблица 6.1

(N, k)	pош	2	−(N−k )	1− 2	−(N−k)	1−(2	−k	−2	−N	)
(7,4)	0.05	0.125		0.875		0.94532
(15,11)	0.05	0.063		0.937		0.99954
(31,26)	0.05	0.031		0.969		0.99999

7.Сопоставить полученные C ДСКС с пропускной способностью канала без контроля ДСК при тех же исходных данных.

8.Результаты отразить в лабораторном отчете.

______________________________________________________________

*Для более быстрого достижения цели оценки C производить на боковых гранях "куба".

61

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Чем вызвана необходимость согласования сигнала с каналом передачи информации?

2.Что понимается под скоростью передачи информации и пропускной способностью канала?

3.Что характеризует матрица переходных вероятностей?

4.Каким образом вычисляется пропускная способность дискретного канала с помехами?

5.Что понимается под стационарным каналом без памяти?

6.В чем сущность теоремы Шеннона для дискретного канала с помехами?

7.Какими свойствами обладают каналы, симметричные по входу и выходу?

8.Каким образом можно оценить ненадежность передачи?

9.Как можно оценить условную вероятность обнаружения ошибки при заданной избыточности?

10.Как можно оценить условную вероятность правильной коррекции ошибки при заданной избыточности?

Лабораторная работа 7

КОРРЕКТИРУЮЩИЕ КОДЫ БОУЗА–ЧОУДХУРИ–ХОКВИНГЕМА

Цель: изучить принципы построения наиболее эффективных циклических кодов, исправляющих ошибки произвольной кратности.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Из основной теоремы Шеннона следует, что если по каналу передавать информацию со скоростью, не превышающей его информационную пропускную способность, то существует такой способ кодирования, при котором сообщения могут быть переданы с произвольно малой ненадежностью.

В теореме не затрагивается вопрос о путях построения кода, обеспечивающего указанную идеальную передачу. Тем не менее, значение ее огромно, поскольку, обосновав принципиальную воз-

62

можность такого кодирования, она мобилизовала усилия специалистов на разработку конкретных кодов.

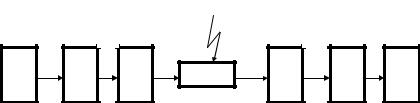
Способность кода обнаруживать и исправлять ошибки, обусловлена наличием избыточных символов. На вход кодирующего устройства канала поступает последовательность из k информационных двоичных символов. На выходе ей соответствует последовательность из N двоичных символов, причем N > k (рис. 7.1).

E(x)

k

ИИКДии

N N

КДк Канал

A(x) A*(x)

k

ДКк ДКии ПИ

Рис. 7.1. Средства помехоустойчивого кодирования

Всего может быть 2 k различных входных последовательностей

и 2 N	различных выходных последовательностей. Из общего числа
2 N	выходных последовательностей только 2 k соответствует

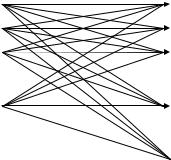
входным (назовем их разрешенными кодовыми комбинациями). Остальные 2N − 2k возможных выходных последовательностей для передачи не используются (назовем их запрещенными кодовыми комбинациями). Возможные трансформации разрешенных кодовых комбинаций при прохождении по каналу с помехами представлены на рис. 7.2.

Число возможных последовательностей длины N, очевидно, больше, чем число возможных последовательностей длины k. Следовательно, множество всех последовательностей длины N может быть разбито на k непустых классов, и каждому классу сопоставлена одна из входных последовательностей длины k. Можно так закодировать последовательность длины k (выбрать представителя соответствующего класса последовательностей длины N), что воздействие ошибок на выбранную последовательность длины N в канале выводит ее из соответствующего ей класса с вероятностью сколь угодно малой. Это позволяет определить на приемной стороне канала, к какому классу принадлежит искаженная ошибками

63

принятая последовательность длины N, тем самым точно восстановить исходную последовательность символов длины k.

A1

A2 A3

...

A2 k

A1* A2*

A3*

...

A*

2 k

...

A2*N

Разрешенные

комбинации

Запрещенные

комбинации

Рис. 7.2. Комбинации возможных переходов вследствие ошибок

Коды Боуза–Чоудхури–Хоквингема (БЧХ), как одни из самых эффективных кодов, исправляющих ошибки произвольной кратности, нашли широкое применение в практике помехоустойчивого кодирования. Однако процедура их построения для заданной длины кода N и максимальной кратности исправляемых ошибок T достаточно трудоемкая.

Изложим кратко принципы, лежащие в основе построения корректирующих кодов БЧХ. Эти коды – разновидность циклических кодов, которые определяются через элементы расширенного поля Галуа. Полем называется множество с двумя определенными на нем операциями – сложением и умножением. Поле с q элементами, если оно существует, называется конечным полем или полем Галуа и обозначается через GF(q). Примитивный элемент поля GF(q) – это такой элемент α поля, все элементы которого, за исключением нуля, могут быть представлены в виде степени элемента α. Подмножество GF(e) в GF(q) называется подполем, если оно само является полем относительно наследуемых из GF(q) операций. В этом случае исходное поле GF(q) называется расширением поля

GF(e).

Пусть GF(e) – некоторое поле, GF(q) – расширение поля GF(e), построенное по примитивному многочлену p(z), и β – элемент

64

GF(q). Тогда простой многочлен F(x) наименьшей степени над GF(e), для которого F (β) mod p(z) ≡ 0 , называется минимальным

многочленом элемента β над GF(e).

В табл. 7.1 задано представление поля GF (24 ) как расширение

поля			GF(2),		построенное			по	примитивному многочлену
p(z) = z 4 + z + 1 .
										Таблица 7.1
			Поле GF (24 )			в виде				Минимальные многочлены
										при αi
	Степени				Многочлена			Кода
	0			0				0000
	α			1				0001		x +1
	α 1			z				0010		F1(x) = x4 +x +1
	α 2			z2				0011		x4 +x +1
	α	3		z3				0100		F3 (x) = x4 +x3 +x2 +x +1
	α 4			z +1				0011		x4 +x +1
	α	5		z2 +z				0110		F5(x) = x2 +x +1
	α	6		z3	+z2			1100		x4 +x3 +x2 +x +1
	α	7		z3	+z +1			1011		F7 (x) = x4 +x3 +1
	α 8			z2 +1				0101		x4 +x +1
	α	9		z3	+z			1010		x4 +x3 +x2 +x +1
	α 10			z2 +z +1				0111		x2 +x +1
	α 11			z3 +z2 +z				1110		x4 +x3 +1
	α 12			z3 +z2 +z +1				1111		x4 +x3 +x2 +x +1
	α 13			z3 +z2 +1				1101		x4 +x3 +1
	α 14			z3 +1				1001		x4 + x3 +1
В нее включены также минимальные многочлены над GF(2) для
всех элементов из поля						GF (2 4 ) , где α = z – примитивный эле-
мент			GF (2 4 ) . Пусть β = z3						– элемент GF (24 ) . Тогда

65

F(x) = x4 +x3 +x2 +x +1		– минимальный многочлен элемента z3
над	GF(2),	так	как	F (β) mod p(z) =

= [(z3 )4 + (z3 )3 + (z3 )2 + (z3 ) +1]mod( z4 + z +1) ≡ 0 .

Коды БЧХ строятся по заданным N и T. Значение k (число информационных разрядов) неизвестно, пока не найден порождающий многочлен кода G(x). В общем случае

G(x) = НОК[F1*C0 (x), F3*C0 (x),..., Fi*C0 (x),..., FФ*С0 (x)] ,

где Ф ≤ D − 2 , D ≥ 2T +1 ( D – минимальное расстояние Хэммин-

га кода БЧХ). Отметим, что минимальные многочлены для любой четной степени всегда уже содержатся в одной из предыдущих строк табл. 7.1. Длина кода БЧХ, как правило, определяется из вы-

ражения N = 2m −1, где m – любое целое число. Иногда возникает ситуация, когда вычисленное по формуле m = log 2 (N +1) получается не целым. Тогда необходимо пользоваться формулой m = log 2 (NC0 + 1) , подбирая минимальное C 0 такое, чтобы результат оказался целочисленным. Число проверочных разрядов кода БЧХ r ≤ mT , отсюда число информационных разрядов

k ≥ 2m −1 −mT . C0

	Если r >	2 m − 1		, то код БЧХ не определен, так как число прове-
		C0

рочных разрядов не может быть больше длины кода.

Например, порождающий многочлен кода длины N=21, служащий для исправления двукратных ошибок T=2, получается сле-

дующим образом. Формула m = log 2 (N +1) к положительным результатам не приводит, а формула m = log 2 ( NC0 + 1) при C0

дает m=6. Далее обращаемся к таблице минимальных многочленов (табл. 7.2), которая строится из таблиц, аналогичных табл. 7.1, но при разных значениях m. Выбираем из табл. 7.2 минимальные мно-

66

гочлены F1 (x) и F3 (x) , так как D −2 = 3 . Умножаем индексы выбранных многочленов на C0 и окончательно получаем

G(x) = НОК[F3 (x), F9 (x)] =

= НОК[x6 + x4 + x2 + x +1, x3 + x2 +1] =

= x9 + x8 + x7 + x5 + x4 + x +1.

Следовательно, r = deg G(x) = 9 и k = 12 . Строки образующей матрицы кода (21,12) находятся как остаток от деления произ-

ведения x j G (x )						на двучлен x N +1 (рис. 7.3).
			2							Таблица 7.2
	m						3	4	5		6 (T)
		1	111 (1)				1011 (1)	10011 (1)	100101	(1)	1000011	(1)
		3					1101 (3)	11111 (2)	111101	(2)	1010111	(2)
		5					1	111 (3)	110111	(3)	1100111	(3)
	i	7						11001 (7)	101111	(5)	1001001	(4)
		9						1	101001	(7)	1101	(5)
		11						1	111011	(15)	1101101	(6)
		13						1	1		1011011	(7)
		15							1		1110101	(10)
		17									1100111	(10)
		19									1011011	(10)
					000000000001:110110011
					000000000010:011010101
					000000000100:110101010
					000000001000:011100111
					000000010000:111001110
M21,12		=			000000100000:000101111
					000001000000:001011110				Рис. 7.3. Образующая матрица
					000010000000:010111100				кода БЧХ (21,12)
					000100000000:101111000
					001000000000:101000011
					010000000000:100110101
					100000000000:111011001

67

Традиционный подход исправления ошибок достаточно трудо-

емкий, так как получить	T		N		опознавателей не представляется
	∑i=1		i

целесообразным. Воспользуемся следующим алгоритмом декодирования. Допустим, что передавалась кодовая комбинация A(x), построенная на основе образующей матрицы кода БЧХ (N, k) с порождающим многочленом G(x), способным исправлять ошибки кратности T включительно. В результате воздействия помех в канале связи в приемнике получена комбинация A*(x)=A(x)+E(x), где E(x) – многочлен ошибки. Делим A*(x) на G(x) и вычисляем вес W полученного остатка. Если W>T, производим циклический сдвиг предыдущего делимого влево на один разряд и опять выполняем деление на многочлен G(x). Эта процедура повторяется до получения остатка с весом не больше T. Если W≤T, складываем последнее делимое с полученным остатком и производим циклический сдвиг полученной комбинации вправо на столько разрядов, на сколько осуществлялся сдвиг влево. Получаем истинную переданную комбинацию.

Процесс исправления ошибок для кода (21,12) представлен на рис. 7.4.

Программные средства построения кодов БЧХ реализуют вышеприведенные процедуры и предназначены для проектирования кодов БЧХ умеренных длин, так как при больших длинах они становятся не лучшими из известных кодов. Целесообразность создания программных средств следует, главным образом, из того, что полное понимание кодов БЧХ, по всей видимости, является наилучшей отправной точкой для изучения многих других классов кодов.

ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ

1.Изучить теоретический материал.

2.Построить порождающий многочлен

G(x) = НОК[F1*C0 (x), F3*C0 (x),..., Fi*C0 (x),..., FФ*С0 (x)]

и образующую матрицу

68

			I T	:
M	N ,k	=		: B
			k ,k	N −k ,k
				:

кода БЧХ со следующими параметрами: N=7, T=2.

3.Продемонстрировать процесс исправления построенным кодом произвольной двукратной ошибки, задаваемой вектором E(x).

4.Отразить подготовку в лабораторном отчете.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Используя обучающие средства диалоговой программы, изучить принципы построения кодов БЧХ.

2.Построить порождающие многочлены

Передаваемое сообщение:

A(X)= 110000000000011101100.

Кратность ошибки: T= 2.

Вектор ошибки:

E(X)= 110000000000000000000.

В результате действия помех в канале связи на приемном конце была принята комбинация:

A"(X)=000000000000011101100.

Проводим деление принятой комбинации на G(X) .

Цикл N 1

Остаток : 11101100 с весом W = 5.

Т.к. W>T ,то надо произвести циклический сдвиг A"(X) влево на 1 разряд и снова произвести деление на G(X) .

Цикл N 2

Остаток : 111011000 с весом W = 5.

Т.к. W>T ,то надо произвести циклический сдвиг A"(X) влево на 1 разряд и снова произвести деление на G(X) .

Цикл N 3

Остаток : 11 с весом W = 2.

Теперь, когда W ≤ T , можно произвести сложение по модулю 2 циклически сдвинутой комбинации A"(X) и полученного остатка.

Комбинация A"(Х) ,циклически сдвинутая влево на 2 разряда: 000000000001110110000.

Сумма циклически сдвинутой комбинации A"(X) и полученного остатка: 000000000001110110011.

Наконец, проведем обратный циклический сдвиг этой суммы вправо на 2 разряда.

Вы получили переданное сообщение: 110000000000011101100.

Рис.7.4. Процесс исправления ошибок

69

G(x) = НОК[F1*C0 (x), F3*C0 (x),..., Fi*C0 (x),..., FФ*С0 (x)]

и образующие матрицы

			I T	:
M	N ,k	=		: B
			k ,k	N −k ,k
				:

ряда кодов БЧХ. Значения длин кодов N задаются преподавателем, параметр T выбирается произвольно.

3.Для каждого кода БЧХ длиной N определить максимальную кратность исправляемых ошибок T.

4.Выполнить основные этапы процесса исправления ошибок. Исходные коды A(x) и векторы ошибок E(x) выбираются произвольно.

5.Результаты отразить в лабораторном отчете.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Какие коды называются корректирующими?

2.В чем сущность помехоустойчивого кодирования?

3.Как определяется минимальное расстояние Хэмминга между кодовыми комбинациями?

4.Какова связь обнаруживающей способности кода с минимальным расстоянием Хэмминга?

5.Какова связь корректирующей способности кода с минимальным расстоянием Хэмминга?

6.Каким образом строится образующая матрица циклического

кода?

7.Какие требования предъявляются к порождающему многочлену циклического кода БЧХ?

8.Сколько разрешенных комбинаций имеет циклический код с образующей матрицей |1:111111|?

9.Какова максимальная кратность исправляемой ошибки циклического кода (7,1)?

10.Дайте определение минимального многочлена.

11.Покажите связь числа проверочных разрядов кода БЧХ с числом информационных разрядов.

70