Зайцев Применение методов Дата Мининг для поддержки процессов управления ИТ-услугами.Учебное пособие 2009

. (2.2)

Множества T1, T2, …, Tn получены при разбиении исходного множества T по проверке X. Выбирается атрибут, дающий максимальное значение по критерию (2.1). Впервые эта мера была предложена Р. Куинленом в разработанном им алгоритме ID3. Кроме вышеупомянутого алгоритма C4.5, есть еще целый класс алгоритмов, которые используют этот критерий выбора атрибута.

Статистический критерий. Алгоритм CART использует так называемый индекс Gini (в честь итальянского экономиста Corrado Gini), который оценивает «расстояние» между распределениями классов.

,

(2.3)

где c – текущий узел; pj – вероятность класса j в узле c.

Этот алгоритм был предложен Л. Брейманом (L. Breiman) и др. [19].

Правило остановки. В дополнение к основному методу построения деревьев решений были предложены различные эвристические правила, улучшающие процедуру построения. В первую очередь, это:

а) использование статистических методов для оценки целесообразности дальнейшего разбиения, так называемая «ранняя остановка». В конечном счете «ранняя остановка» процесса построения привлекательна в плане экономии времени обучения, но здесь уместно сделать одно важное предостережение: этот подход строит менее точные классификационные модели и поэтому ранняя остановка крайне нежелательна. Признанные авторитеты в этой области Л. Брейман и Р. Куинлен советуют «вместо остановки использовать отсечение»;

b)ограничение глубины дерева. Необходимо остановить дальнейшее построение, если разбиение ведет к дереву с глубиной превышающей заданное значение;

c)разбиение должно быть нетривиальным, т.е. получившиеся в результате узлы должны содержать не менее заданного количества примеров.

21

Список дополнительных правил можно продолжить, т.к. на сегодняшний день не существует одного такого, которое бы имело наибольшую практическую ценность. К выбору и использованию правил следует подходить осторожно, из-за того, что многие из них эффективны только в каких-то частных случаях.

Правило отсечения. Очень часто алгоритмы построения деревьев решений формируют сложные деревья, которые «переполнены данными», имеют много узлов и ветвей. Такие «ветвистые» деревья очень трудны для понимания и анализа. К тому же ветвистое дерево, имеющее много узлов, разбивает обучающее множество на все большее количество подмножеств, состоящих из все меньшего количества объектов.

Ценность правила, справедливого скажем для 2-3 объектов, крайне низка, и в целях анализа данных такое правило практически непригодно. Гораздо ценнее иметь дерево, состоящее из небольшого количества узлов, которым бы соответствовало большое количество объектов из обучающей выборки. И тут возникает вопрос: а не построить ли все возможные варианты деревьев, соответствующие обучающему множеству, и из них выбрать дерево с наименьшей глубиной? К сожалению, это задача является NP-полной, как было показано Л. Хайфилем и Р. Ривестом и, как известно, этот класс задач не имеет эффективных методов решения.

Для решения вышеописанной проблемы часто применяется так называемое отсечение ветвей.

Пусть под точностью (распознавания) дерева решений понимается отношение правильно классифицированных объектов при обучении к общему количеству объектов из обучающего множества, а под ошибкой – количество неправильно классифицированных. Предположим, что нам известен способ оценки ошибки дерева, ветвей и листьев. Тогда возможно использовать следующее простое правило:

1)построить дерево;

2)отсечь или заменить поддеревом те ветви, которые не приведут к возрастанию ошибки (рис. 2.2).

Вотличие от процесса построения, отсечение ветвей происходит снизу вверх, двигаясь с листьев дерева, отмечая узлы как листья, либо заменяя их поддеревом.

22

Рис. 2.2. Пример дерева решений до и после отсечения

Хотя отсечение не является панацеей, но в большинстве практических задач дает хорошие результаты, что позволяет говорить о правомерности использования подобной методики.

Правила. Иногда даже усеченные деревья могут быть все еще сложны для восприятия. В таком случае можно прибегнуть к методике извлечения правил из дерева с последующим созданием наборов правил, описывающих классы.

Для извлечения правил необходимо исследовать все пути от корня до каждого листа дерева. Каждый такой путь даст правило, где условиямибудутявлятьсяпроверкиизузлов, встретившихсянапути.

2.2. Анализ возможностей и ограничений метода деревьев решений

При помощи метода деревьев решений аналитик может быстро получить правила вида "Из A следует B" [16].

Однако существующие алгоритмы этого метода сталкиваются с невозможностью решения некоторых задач. Например, задача

IF (X1 > 4) & (X2 < 5) THEN Класс 1; IF (X1 < 5) & (X2 > 4) THEN Класс 1; IF (X1 < 5) & (X2 < 5) THEN Класс 2; IF (X1 > 4) & (X2 > 4) THEN Класс 2

не решается методом деревьев, так как ни один из выбранных признаков (X1, X2) отдельно не дает возможности разделить классы. Эта проблема называется проблемой сегментация признаков. Более подробно проблемы построения деревьев решений изложены в ра-

боте [16].

23

Области эффективного применения метода деревьев реше-

ний. При помощи алгоритма выявления деревьев решений можно решать достаточно большой спектр практических задач:

•задачи описания данных: деревья решений позволяют хранить информацию о данных в компактной форме, вместо них мы можем хранить дерево решений, которое содержит точное описание объектов [29, 33];

•задачи классификации: деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения [20, 22, 33];

•задачи регрессии: если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых (входных) переменных. Например, к этому классу относятся задачи численного прогнозирования (предсказания значений целевой переменной) [33].

2.3. Алгоритм С 4.5

Прежде чем приступить к описанию алгоритма построения дерева решений, определим обязательные требования к структуре данных и непосредственно к самим данным [32], при выполнении которых алгоритм C4.5 будет работоспособен.

1.Описание атрибутов. Данные, необходимые для работы алгоритма, должны быть представлены в виде плоской таблицы. Вся информация об объектах (далее примеры) из предметной области должна описываться в виде конечного набора признаков (далее атрибуты). Каждый атрибут должен иметь дискретное или числовое значение. Сами атрибуты не должны меняться от примера к примеру, и количество атрибутов должно быть фиксированным для всех примеров.

2.Определенные классы. Каждый пример должен быть ассоциирован с конкретным классом, т.е. один из атрибутов должен быть выбран в качестве метки класса.

3.Дискретные классы. Классы должны быть дискретными. Каждый пример должен однозначно относиться к конкретному классу. Случаи, когда примеры принадлежат к классу с вероятностны-

24

ми оценками, исключаются. Количество классов должно быть значительно меньше количества классифицируемых примеров.

Алгоритм построения дерева. Пусть задано множество примеров T, и каждый элемент этого множества описывается m атрибутами. Количество примеров во множестве T будем называть мощностью этого множества и будем обозначать |T |. Пусть метка класса принимает следующие значения C1, C2 …, Ck.

Наша задача заключается в построении иерархической классификационной модели в виде дерева из множества примеров T. Процесс построения дерева будет происходить сверху вниз. Сначала создается корень дерева, затем потомки корня и т.д.

На первом шаге мы имеем пустое дерево (только корень) и исходное множество T (ассоциированное с корнем). Требуется разбить исходное множество на подмножества. Это можно сделать, выбрав один из атрибутов в качестве проверки. Тогда в результате разбиения получаются n (по числу значений атрибута) подмножеств и, соответственно, создаются n потомков корня, каждому из которых поставлено в соответствие свое подмножество, полученное при разбиении множества T. Затем эта процедура рекурсивно применяется ко всем подмножествам (потомкам корня) и т.д.

Рассмотрим подробнее критерий выбора атрибута, по которому должно пойти ветвление. Очевидно, что в нашем распоряжении m (по числу атрибутов) возможных вариантов, из которых мы должны выбрать самый подходящий. Некоторые алгоритмы исключают повторное использование атрибута при построении дерева, но в нашем случае мы таких ограничений накладывать не будем. Любой из атрибутов можно использовать неограниченное количество раз при построении дерева.

Пусть мы имеем проверку X (в качестве проверки может быть выбран любой атрибут), которая принимает n значений A1, A2, …, An. Тогда разбиение T по проверке X даст нам подмножества T1, T2, …, Tn при X, равном, соответственно, A1, A2, …, An. Единственная доступная нам информация – то, каким образом классы распределены в множестве T и его подмножествах, получаемых при разбиении по X. Именно этим и воспользуемся при определении критерия.

Пусть freg(Cj, S) – количество примеров из некоторого множества S, относящихся к одному и тому же классу Cj. Тогда вероят-

25

ность того, что случайно выбранный пример из множества S будет принадлежать к классу Cj

.

Согласно теории информации, количество содержащейся в сообщении информации, зависит от ее вероятности

. (2.4)

Поскольку мы используем логарифм с двоичным основанием, то выражение (2.4) дает количественную оценку в битах.

Выражение

(2.5)

дает оценку среднего количества информации, необходимого для определения класса примера из множества T. В терминологии теории информации выражение (2) называется энтропией множества T.

Ту же оценку, но только уже после разбиения множества T по X, дает выражение:

. (2.6)

Тогда критерием для выбора атрибута будет являться следующая формула:

Gain(X) = Info(T) – Infox(T).

(2.7)

Критерий (2.7) считается для всех атрибутов. Выбирается атрибут, максимизирующий данное выражение. Этот атрибут будет являться проверкой в текущем узле дерева, а затем по этому атрибуту производится дальнейшее построение дерева. Таким образом, в узле будет проверяться значение по этому атрибуту, и дальнейшее движение по дереву будетпроизводитьсявзависимостиотполученногоответа.

Такие же рассуждения можно применить к полученным подмножествам T1, T2, …, Tn и продолжить рекурсивно процесс построения дерева, до тех пор, пока в узле не окажутся примеры из одного класса.

26

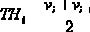
Важное замечание. Если в процессе работы алгоритма получен узел, ассоциированный с пустым множеством (т.е. ни один пример не попал в данный узел), то он помечается как лист, и в качестве решения листа выбирается наиболее часто встречающийся класс у непосредственного предка данного листа.

Здесь следует пояснить, почему критерий (2.7) следует максимизировать. Из свойств энтропии нам известно, что максимально возможное значение энтропии достигается в том случае, когда все его сообщения равновероятны. В нашем случае, энтропия (2.6) достигает своего максимума, когда частота появления классов в примерах множества T равновероятна. Нам же необходимо выбрать такой атрибут, чтобы при разбиении по нему один из классов имел наибольшую вероятность появления. Это возможно в том случае, когда энтропия (2.6) будет иметь минимальное значение и, соответственно, критерий (2.7) достигнет своего максимума.

Как быть в случае с числовыми атрибутами? Понятно, что следует выбрать некий порог, с которым должны сравниваться все значения атрибута. Пусть числовой атрибут имеет конечное число значений. Обозначим их {v1, v2, …, vn}. Предварительно отсортируем все значения. Тогда любое значение, лежащее между vi и vi+1, делит все примеры на два множества: те, которые лежат слева от

этого значения {v1, v2, …, vn}, и те, что справа {vi+1, vi+2, …, vn}. В качестве порога можно выбрать среднее между значениями vi и vi+1:

.

Таким образом, мы существенно упростили задачу нахождения порога, и привели к рассмотрению всего n-1 потенциальных пороговых значений TH1, TH2, …, THn-1. Формулы (2.5), (2.6) и (2.7) последовательно применяются ко всем потенциальным пороговым значениям, и среди них выбирается то, которое дает максимальное значение по критерию (2.7). Далее это значение сравнивается со значениями критерия (2.7), подсчитанными для остальных атрибутов. Если выяснится, что среди всех атрибутов данный числовой атрибут имеет максимальное значение по критерию (2.7), то в качестве проверки выбирается именно он.

Следует отметить, что все числовые тесты являются бинарными, т.е. делят узел дерева на две ветви.

27

Классификация новых примеров. Итак, мы имеем дерево ре-

шений и хотим использовать его для распознавания нового объекта. Обход дерева решений начинается с корня дерева. На каждом внутреннем узле проверяется значение объекта Y по атрибуту, который соответствует проверке в данном узле, и, в зависимости от полученного ответа, находится соответствующее ветвление, и по этой дуге двигаемся к узлу, находящему на уровень ниже и т.д. Обход дерева заканчивается, как только встретится узел решения, который и дает название класса объекта Y.

Далее можно легко получить дерево решений, реализовав описанный алгоритм. Правда, небольшим недостатком будут ветвистые деревья, если примеры представлены очень большим количеством атрибутов. Этот недостаток можно устранить, применив методику отсечения ветвей.

Улучшенный критерий разбиения. Критерий (2.7) имеет один недостаток – он «предпочитает» атрибуты, которые имеют много значений. Рассмотрим гипотетическую задачу медицинской диагностики, где один из атрибутов идентифицирует личность пациента. Поскольку каждое значение этого атрибута уникальное, то при разбиении множества примеров по этому атрибуту получаются подмножества, содержащие только по одному примеру. Так как все эти множества «однопримерные», то и пример относится, соответственно, к одному единственному классу, тогда

InfoX (T) = 0.

Значит, критерий (2.7) принимает свое максимальное значение, и несомненно, что именно этот атрибут будет выбран алгоритмом. Однако, если рассмотреть проблему под другим углом – с точки зрения предсказательных способностей построенной модели, то становится очевидным вся бесполезность такой модели. Хотя на практике не так часто встречаются подобные задачи, но, тем не менее, необходимо предусмотреть и такие случаи.

Эта проблема решается введением некоторой нормализации. Пусть суть информации сообщения, относящегося к некоторому примеру, указывает не на класс, к которому пример принадлежит, а на выход. Тогда, по аналогии с определением Info(T), мы имеем:

. (2.8)

28

Выражение (2.8) оценивает потенциальную информацию, получаемую при разбиении множества T на n подмножеств.

Рассмотрим следующее выражение:

. (2.9)

Пусть выражение (2.9) является критерием выбора атрибута. Очевидно, что атрибут, идентифицирующий пациента, не будет высоко оценен критерием (2.9). Пусть имеется k классов, тогда числитель выражения (2.9) максимально будет равен log2(k) и пусть n – количество примеров в обучающей выборке и одновременно количество значений атрибута, тогда знаменатель максимально равен log2(n). Если предположить, что количество примеров заведомо больше количества классов, то знаменатель растет быстрее, чем числитель, и, соответственно, выражение будет иметь небольшое значение. Таким образом, можем заменить критерий (2.7) на новый критерий (2.9), и опять же выбрать тот атрибут, который имеет максимальное значение по критерию. Критерий (2.7) использовался в алгоритме ID3, критерий

(2.9) введенвмодифицированномалгоритмеС4.5.

Несмотря на то, что мы улучшили критерий выбора атрибута для разбиения, алгоритм может создавать узлы и листья, содержащие незначительное количество примеров. Чтобы избежать этого, следует воспользоваться еще одним эвристическим правилом: при разбиении множества T по крайней мере два подмножества должны иметь не меньше заданного минимального количества примеров k (k > 1); обычно оно равно двум. В случае невыполнения этого правила, дальнейшее разбиение этого множества прекращается, и соответствующий узел отмечается как лист.

Вероятно, что при таком ограничении может возникнуть ситуация, когда примеры, ассоциированные с узлом, относятся к разным классам. В качестве решения листа выбирается класс, который наиболее часто встречается в узле, если же примеров равное количество из всех классов, то решение дает наиболее часто встречающийся класс у непосредственного предка данного листа.

Возвращаясь к вопросу о выборе порога для числовых атрибутов, можно ввести следующее дополнение: если минимальное число примеров в узле k, тогда имеет смысл рассматривать только сле-

29

дующие значения TH1, TH2, …, THn-1, так как при разбиении по первым и последним k – 1 порогам в узел попадает меньше k примеров.

Пропущенные данные. Алгоритм построения деревьев решений, рассматриваемый нами, предполагает, что для атрибута, выбираемого в качестве проверки, существуют все значения, хотя явно это нигде не утверждалось. Таким образом, для любого примера из обучающей выборки существует значение по этому атрибуту.

Пока мы работаем с синтетическими данными, особых проблем не возникает, можем «сгенерировать» нужные данные. Но как только обратимся к практической стороне вопроса, то выясняется, что реальные данные далеки от идеальных, и что часто встречаются пропущенные, противоречащие и аномальные данные.

Остановимся подробнее на проблеме пропущенных данных. Первое решение, которое лежит на поверхности и само напрашивается – не учитывать примеры с пропущенными значениями. Следует подчеркнуть, что крайне нежелательно отбрасывать весь пример только потому, что по одному из атрибутов пропущено значение, поскольку мы рискуем потерять много полезной информации.

Тогда нам необходимо выработать процедуру работы с пропущенными данными.

Пусть T – множество обучающих примеров и X – проверка по некоторому атрибуту A. Обозначим через U количество неопределенных значений атрибута A. Изменим формулы (2.5) и (2.6) таким образом, чтобы учитывать только те примеры, у которых существуют значения по атрибуту A:

, (2.10)

.

(2.11)

В этом случае при подсчете freq(Cj, T) учитываются только примеры с существующими значениями атрибута A.

Тогда критерий (2.7) можно переписать:

.

(2.12)

30