Кнопова Избранные главы математики в примерах и задачах.Учебное пособие 2009

Пример 3.8. Определить интервалы выпуклости функции y = x3

и найти точки перегиба.
Решение. f ′(x) =3x2 ; f ′′(x) = 6x .
Точки перегиба находим из уравнения			f ′′(x) = 0 . Имеем одну
точку перегиба x = 0 . При	x > 0	f ′′(x) > 0 , значит на промежутке
(0, +∞) функция f (x) = x3	вогнутая. При		x < 0 f ′′(x) < 0 и f (x)
будет выпуклой вверх при x (−∞,		0) .

Пример 3.9. Пользуясь правилом Лопиталя, найти

lim x3 −8 .

x→2 x2 −4

Решение. При x = 2 числитель и знаменатель рассматриваемой дроби обращаются в нуль. Для того, чтобы раскрыть эту неопределенность, воспользуемся правилом Лопиталя

lim	ϕ(x)	= lim	ϕ′(x)
x→a ψ(x)		x→a ψ′(x)

и получим

lim	x3 −8	= lim	(x3 −8)′	= lim	3x2	=	3	lim x =3 .
	x2 −4		(x2 −4)′		2x
x→2		x→2		x→2			2 x→2

ЗАДАЧИ

Найти интервалы монотонности функций.

54.	f (x) = −2x2 +3.	55.	f (x) = x5.
56.	f (x) = x3 −3x .	57.	f (x) = (x2 −4)2.

Определить интервалы выпуклости функции f (x) и найти точ-

ки перегиба.
58.	f (x) = x2 −10 .	59.	f (x) = x5 −3x .
60.	f (x) = x3 −6x2 + 2x +1 .	61.	f (x) = x4 −2x3 +6x −4 .

20

Исследовать на экстремум функции.

62.	f (x) = x3 −27x .	63. f (x) = x3 −9x2 +24x −12 .
64.	f (x) = (x2 −4)2.

Найти наибольшее и наименьшее значение функции f (x) на отрезке.

65.	f (x) = x2 −4x +3, x [0,	3] .
66.	f (x) = x3 −3x2 −9x +35,	x [−4, 4] .

67.Периметр прямоугольного участка равен 128 м. Какова максимальная возможная площадь этого участка?

68.Нужно огородить с трех сторон участок прямоугольной формы, прилегающий к длинной стене. Из имеющегося материала можно сделать забор длиной 120 м. Каковы должны быть размеры забора, чтобы площадь, обнесенная им, была наибольшей?

69.Разложить число 30 на два слагаемых так, чтобы их произведение было наибольшим.

Используя правило Лопиталя, найти следующие пределы.

70.	lim tg x .			71.	lim	1−cos x .
	x→0		x		x→0	sin x
72.	lim		ln x .	73.	lim	1−cos x .
	x→+∞		x		x→0	tg x
74.	lim	1−cos x .		75.	lim sin 3x .
	x→0		x		x→0 sin 5x
76.	lim tg 3x .			77.	lim cos x −cos 3x .
	x→0	tg x			x→0	x2
78.	lim	1−cos x .
	x→0		x2

21

4. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

4.1. Неопределенные интегралы

Основные интегралы

C = const;						k = const.
	∫kdx = kx +C ;
∫ xa dx =		xa+1			+C, a ≠ −1;
		a +1
	∫ dx			= ln				x		+C ;
	x
∫ax dx =	a x			+C,						a > 0, a ≠1;
	ln a

∫ex dx = ex +C ;

∫cos x dx =sin x +C ;

∫sin x dx = −cos x +C ;

∫cosdx2 x = tg x +C ;

∫sindx2 x = −ctg x +C .

Пример 4.1. Вычислить ∫(x2 +7x −5)dx .

Решение.

∫(x2 +7x −5)dx = ∫ x2dx + ∫7xdx −∫5dx = x3 + 7x2 −5x +C .

3 2

При интегрировании сложной функции пользуются методом замены переменной:

22

	∫	f (g(x))g′(x)dx = ∫f (z)dz ,	(4.1)
где z = g(x) ,	а dz = g′(x)dx .
Пример 4.2. Вычислить ∫sin 3x dx .
Решение.	Введем	новую переменную z =3x , тогда	dz =

= (3x)′ dx =3dx , откуда dx = dz3 .

Этот интеграл можно переписать в новых обозначениях так, что он становится "табличным":

∫sin 3x dx = ∫sin z dz3 = −13 cos z +C = −13 cos 3x +C .

На последнем шаге мы вернулись к прежней переменной, т.е. вместо z подставили ее выражение через x (z =3x) .

Пример 4.3. Найти ∫(2x +3)2dx .

Решение. Делаем замену переменных z = 2x +3 ,

		dz = (2x +3)′ dx =		2dx,			dx =	dz	.
	Тогда имеем						2
	∫(2x +3)	2dx = ∫ z2 dz	= 1		z3	+C = 1 (2x +3)2				+C .
				3
		2	2				6
	Формула интегрирования по частям:
	∫u(x) v′(x)dx =u(x) v(x) −∫u′(x) v(x)dx .									(4.2)

Пример 4.4. Найти ∫x exdx .

Решение. Положим u(x) = x , а v′(x) = ex. Тогда v(x) = ex. Применяя формулу интегрирования по частям (4.2), с учетом того, что u′(x) = x′ =1 , имеем

∫x exdx = x ex −∫exdx = x ex −ex +C .

23

ЗАДАЧИ

Вычислить интегралы. 1. ∫ (−7x +4)dx .

3.∫ x2 − 2 dx .

x

	5. ∫		2dx			.
			3
			x
	7. ∫			3	+2				x dx .
		x
	9. ∫ 2xdx .
	11.	∫ cos 5x dx .
	13.	∫ e2x−3dx .
	15.	∫		2dx			.
				4x −1
	17.	∫ 3(5x +2)4dx .
	19.	∫			6dx								.
				(5x −7)						3
	21.	∫			5dx							.
					2x +			7
	23.	∫ cos2 x sin x dx .
	25.	∫	e2x +							3					dx .
										2
									cos					5x
	27.	∫	2 sin					x			+3cos 6x dx .
								5
	29.	∫ x sin x dx .
	31.	∫ x ln x dx .

2. ∫ (2x2 +3x −8)dx . 4. ∫ (4x3 −3x2 +1)dx . 6. ∫ x2(x2 +3)dx .

8. ∫			5							x
					+2e						dx .
			x
10.	∫ e3xdx .
12.	∫ sin(2x +1)dx .
14.	∫		dx			.
		x +1
16.	∫ (2x −5)6dx .
18.	∫			dx							.
		(3x +1)						2
20.	∫ 8(11−3x)5dx .
22.	∫ sin3 x cos x dx .
24.	∫ (1−cos x −cos 2x)dx .
26.	∫		7sin				x			+			2		dx .
													2
				3								cos		4x
28.	∫ x cos x dx .
30.	∫ ln x dx .

24

4.2. Определенные интегралы

Если F(x) – первообразная для f (x) , то справедлива формула

Ньютона – Лейбница, по которой и вычисляется определенный интеграл

	b									b
	∫ f (x)dx = F(x)										= F(b) − F(a) .											(4.3)
	a					2				a
	2		x3					8			1			7
Пример 4.5.	∫ x2 dx =						=		−				=		.
	1	3				1	3				3		3
																	2
	2
Пример 4.6.	∫ (3x2 −2x)dx = (x3 − x2)																	= (8 −4) −0 = 4 .
	0																0
	1
Пример 4.7. Найти ∫ cos 3xdx .
	0
Решение. Делаем замену переменных.																		dx = dz .
	z =3x,	dz = (3x)′dx =3dx,
																					3
Надо изменить пределы интегрирования.																			Так как z =3x ,			то при
x = 0 z = 0, а при x =1		z =3.
1		3											1 sin z							3	1 sin 3 .
∫ cos 3xdx = ∫ cos z dz											=									=
0		0					3						3							0	3

Возвращаться от z к x (к старой переменной) не нужно. Пример 4.8. Интегрирование по частям.

1	1
∫ x ex dx = x ex		10 −∫ ex dx = x ex		10 −ex		10 = e −0 −e +1 =1
0	0

(сравните с примером 4.4).

Пример 4.9. Вычислить площадь фигуры, ограниченной осью 0x и графиком функции y = 2x − x2.

25

Решение. y = 2x − x2 = x(2 − x) –										парабола, которая пересекает
ось 0x в двух точках			x = 0		и	x = 2 , ветви параболы направлены
вниз. Поэтому площадь данной криволинейной трапеции
2						x3			2		8	4		1
S = ∫(2x − x	2			2											.
		)dx = x			−					= 4 −	−0 =	3	=1	3
0						3			0		3

ЗАДАЧИ

Вычислить интегралы.

2

32. ∫ x3 dx .

−1

1

34. ∫(4x3 −3x2 +1)dx .

0

1

36. ∫ (5x9 +8sin x)dx .

−1

1

38. ∫ (5sin 2x + x17)dx .

		−1
		1		dx
	40.	∫					.
			2x +1
		0
		0
	42.	∫		x +1dx .
		−1
		π/8		dx
	44.	∫							.
				cos	2
		0						2x

2

46. ∫e2x−1dx .

1

		1
	33.	∫x5 dx .
		0
		1
	35.	∫ (x2 +5x8)dx .
		−1
		1
	37.	∫(2x −5x)dx .
		0
		3	dx
	39.	∫		.
		2	x −1
		0
	41.	∫	(2x +1)2dx .
		−1/2
		6			x
	43.	∫	2 −			dx .
		3	3
		π
	45.	∫ (cos 2x + x2)dx .
		−π
		2
	47.	∫xex dx .
		0

26

π/2

48. ∫ x sin xdx .

0

49. Найти площадь S, ограниченную графиком кривой y =sin x

иосью 0x, если x [0, π] .

50.Найти площадь S, ограниченную линиями y = 2x и y = x2.

4.3. Несобственные интегралы

+∞

b

∫

f (x)dx = lim

f (x) dx .

(4.4)

b→+∞ ∫

a

a

b

b

∫

f (x)dx = lim

f (x) dx .

(4.5)

a→−∞ ∫

−∞

a

+∞

c

+∞

∫

f (x)dx = ∫

f (x) dx + ∫

f (x)dx .

(4.6)

−∞

−∞

c

+∞

Пример 4.10. Выяснить, сходится или расходится

∫

xdx .

0

+∞

b

x2

b

b2

Решение. ∫ xdx = lim

∫ x dx = lim

=

−0

= +∞.

lim

0

b→+∞

0

b→+∞ 2

0

b→+∞

2

Интеграл расходится.

+∞

Пример 4.11. Вычислить ∫1 dxx2 .

Решение.

+∞ dx

= lim

b dx

=

lim

−

1

b

∫ x2

∫ x2

=

b→+∞

b→+∞

x

1

1

1

= lim

−

1

=1

−

lim

1

=1−0 =1 .

b

+1

x→+∞

b→+∞ b

27

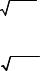
ЗАДАЧИ

Выяснить, сходятся или расходятся следующие несобственные интегралы. Если интеграл сходится, то вычислить его.

1
51. ∫ dx .
0	x
+∞

53.	∫ x2dx .
	0
	0
55.	∫ exdx .
	−∞
	+∞
57.	∫ 5e−3xdx .
	0
	+∞
59.	∫ 2e−4xdx .
	0
	+∞	dx
61.	∫				.
		(x +1)		2
	0
	+∞	dx
63.	∫		.
	0	x +1

+∞

52. ∫1 dxx3 .

+∞

54. ∫ dx .

1 x

0

56. ∫ e2xdx .

−∞

0

58. ∫ e3xdx .

−∞

		0	dx
	60.	∫		.
		−1	x +1
		0	dx
	62.	∫			.
		−4	x + 4

0

64. ∫ x exdx .

−∞

28

5. РЯДЫ

5.1. Числовые ряды

Пусть дан числовой ряд

∞
a1 + a2 + a3 + ... = ∑an ,	(5.1)
n=1
где все an R .
Необходимый признак сходимости числового ряда:
lim an = 0 .	(5.2)
n→+∞

Достаточный признак сходимости числового ряда (признак

	Даламбера):		an+1
	если lim				= q ,
			an
	n→+∞

то при q < 1 ряд (5.1) сходится, а при q > 1 расходится (при q = 1 ряд может как сходиться, так и расходиться).

∞

Пример 5.1. Выяснить, сходится или расходится ряд ∑2n.

n=0

Решение. a

n

= 2n,

lim 2n = +∞ , нарушен необходимый при-

n→+∞

знак сходимости ряда (см. (5.2)), значит этот ряд расходится.

∞

Пример 5.2. Исследовать сходимость ряда ∑

n

.

n

n=1 2

Решение. Воспользуемся признаком Даламбера. Здесь

a

n

=

n

,

a

n+1

=

n +1

,

2n

2n+1

an+1

=

n +1

2n

= 1

n +1 .

2n+1

an

n

2

n

29