Е.Н. Грибанов Теория вероятностей и математическая статистика. Методические указания для студентов всех специальностей

3

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

События в материальном мире можно разбить на три кате-

гории − достоверные, невозможные и случайные. Например,

если подбросить игральную кость, то достоверно, что число выпавших очков будет натуральным числом, невозможно, чтобы это число равнялось 7, и возможно, что оно будет равно 5. Однако при одних бросках это число будет равно 5, а при других будут выпадать другие значения очков: 1, 2, 3, 4 или 6.

Потребности практики привели математиков к изучению случайных событий. Например, при организации телефонной связи в некотором районе нужно знать число вызовов в каждый момент времени, а оно случайным образом изменяется с течением времени. При стрельбе из артиллерийского орудия надо знать число снарядов, попавших в цель, а попадание в цель является случайным событием.

На первый взгляд может показаться, что в задачах о случайных событиях ничего нельзя сказать об их исходе. И действительно, если бросить кость лишь один раз, то с одинаковой вероятностью можно ожидать выпадения 1, 2, 3, 4, 5 или 6 очков. Но при многократном повторении этого опыта оказывается, что одни исходы будут появляться чаще, а другие − реже. Например, если бросить кость 1200 раз, то очень маловероятно, чтобы все время выпадало одно очко. Гораздо вероятнее, что значения 1, 2, 3, 4, 5 и 6 будут появляться примерно с одной и той же частотой.

Раздел математики, изучающий закономерности случайных событий, называют теорией вероятностей. Эта теория имеет дело не с отдельными событиями, а с результатом проведения достаточно большого числа испытаний, т. е. с закономерностями массовых случайных явлений. По определению, приведенному в БСЭ, теория вероятностей есть математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных ка- ким-либо образом с первыми.

В повседневной жизни мы часто пользуемся словами «вероятность», «шанс» и т. д. «К вечеру, вероятно, пойдет дождь», «Вероятнее всего, мы поедем в воскресенье за город», «Это совершенно невероятно», «Много шансов, что я успеш-

4

но напишу контрольную работу» и т. д. − все эти выражения как-то оценивают вероятность того, что произойдет некоторое случайное событие. Однако, чтобы можно было применять к оценке вероятностей математические методы, надо дать этому понятию строгое определение. Мы сделаем это позднее, а сейчас приведем цитату из БСЭ, дающую представление о том, что такое вероятность:

«Вероятность математическая − числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».

f (n +1) = (n +1) f (n), называется n-факториалом и обозначается

n!. Для любого натурального n имеем n! =1 2 K n.

Пример 1. 6! =1 2 3 4 5 6 = 720.

Перестановки. Каждая последовательность n различных элементов с учётом их порядка называется перестановкой этих элементов. Число перестановок обозначается Pn и находится по

формуле Pn = n!.

Пример 2. Сколькими способами можно расставить шесть книг на полке?

Решение. Число способов равно числу перестановок из шести элементов, то есть Pn = 6! = 720 .

Размещение. Любой упорядочный набор k различных элементов множества М, содержащего n элементов, называется размещением k элементов из n. Число размещений обозначается сим-

Пример 3. Сколькими способами можно распределить три первых места для восьми участвующих в соревновании команд?

Решение. Так как нас интересует, какая из команд займёт первое, второе и третье места, то есть порядок среди отобранных

5

трёх команд, используем размещение. Тогда число способов най-

Сочетание. Любое подмножество из k различных элементов множества М, содержащего n элементов, называется сочетанием.

Число сочетаний обозначается символом Cnk и находится по фор-

Пример 4. Найти число способов отобрать три цветка из се-

ми.

Решение. Так как порядок среди цветов нам не важен, то используем сочетание. Число способов найдём по формуле

Случайные события

2. Алгебра событий О. 1. Событие называется случайным, если в результате опы-

та оно может либо произойти, либо не произойти.

О. 2. Событие называется достоверным, если оно обязательно происходит в результате опыта.

О. 3. Событие называется невозможным, если оно не может произойти в данном опыте.

О. 4. События называются несовместными, если они не могут произойти в одном опыте.

О. 5. Событие А благоприятствует событию В, если из появления события А следует, что произошло событие В.

О. 6. События образуют полную группу, если в результате опыта произойдёт хотя бы одно из них.

О. 7. Событие С называется суммой событий А В, если оно состоит в появлении события А или появлении события В. Сумма событий обозначается С = А+ В.

О. 8. Событие С называется произведением событий А В, если оно состоит в появлении события А и появлении события В. Обозначается С = А В.

6

О. 9. Событие С называется разностью событий А В, если оно состоит в появлении события А и не появлении события В. Обозначается С = А- В.

О. 10. Событие А называется противоположным событию А, если оно состоит в не появлении события А.

О. 11. События называются равновозможными, если нет объективных оснований считать, одно более возможным чем другое.

О. 12. Равновозможные, несовместные образующие полную группу события называются исходами данного опыта.

3. Классическое определение вероятности О. 1. Вероятностью события называется численная мера

степени объективной возможности появления этого события.

О. 2. (Классическое определение вероятности) Вероятностью события А называется отношение числа благоприятствующих исходов к общему числу исходов данного опыта.

Вероятность события А обозначается p(A). Тогда p(A) = mn , где

m - число благоприятных для появления события А исходов, n - число всевозможных исходов опыта.

Основные свойства вероятности

1.Вероятность достоверного события равна единице.

2.Вероятность невозможного события равна нулю.

3.Для любого события А его вероятность заключена в интервале 0 ≤ p(A)≤1.

4.Вероятность наступления противоположного события А

равна разности между единицей и вероятностью события А, то есть p(A) = 1 - p(A) .

Пример 5. Из урны, содержащей 12 чёрных и 8 белых шаров, наудачу вынуто два шара. Найти вероятность того, что они разного цвета.

Решение. Обозначим событие А – шары разного цвета, тогда по определению p(A) = mn . Но число всевозможных исходов рав-

но числу способов отобрать два шара из двадцати, то есть n = C202 =1820! !2! = 20219 =190 . Число благоприятных исходов рав-

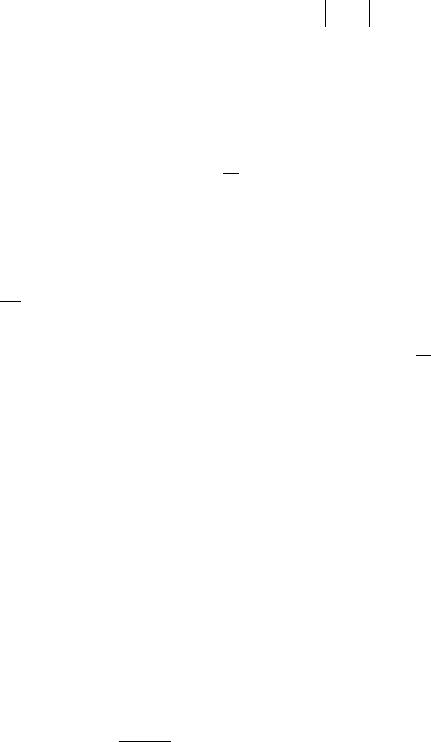
8

(x; y) однозначно определяет время прихода обоих студентов.

Студенты встретятся, если выполнено условие x - y ≤ 14 . Постро-

x − y = −14 y = x + 14 . Область, заключённая между этими ли-

ниями внутри квадрата, составляет область благоприятных исходов события А Рис. 1. Для события Аобласть благоприятных исходов согласно Рис. 1 состоит из двух прямоугольных треуголь-

ников с катетами, равными 6045 = 34 , общей площадью, равной

S = 2 34 34 =169 . Область всевозможных исходов равна площади

квадрата со стороной 1. Следовательно, площадь всевозможных исходов равна Sвс =1 1 =1. Тогда вероятность события A равна

5. Теоремы сложения Т.1. Для несовместных событий вероятность появления сум-

мы событий равна сумме вероятностей. То есть p(A + B)= p(A)+ p(B).

Доказательство. Пусть опыт имеет n исходов, событию А благоприятствует k из них, а событию В − благоприятствует m. Тогда сумме событий А+В благоприятствуют m+k. Тогда

p(A + B)= mn+ k = mn + kn = p(A)+ p(B).

Пример 8. Вероятности получить на экзамене 5, 4, 3 соответственно равны 0,2; 0,3; 0,3. Найти вероятность успешной сдачи экзамена.

Решение. Обозначим события: А – студент успешно сдал экзамен; В; С; К – студент сдал экзамен на 5; 4; 3 соответственно. По условию p(A)= p(B +C + K ). В силу несовместности событий

9

В; С; К и по условию p(B)= 0,2; p(C )= p(K )= 0,3 по теореме имеем p(A)= p(B +C + K )= p(B)+ p(C)+ p(K )=0,2 +0,3 +0,3 =0,8.

Т. 2. Для любых событий вероятность появления суммы этих событий равна сумме вероятностей этих событий без вероятности их совместного появления. То есть p(A+B)= p(A)+ p(B)− p(A B).

вое, получаем окончательно p(A+ B)= p(A)+ p(B)− p(A B).

6. Теоремы умножения О. 1. Два события называются независимыми, если вероят-

ность появления одного из них не зависит от того, произошло или не произошло второе событие.

О. 2. Несколько событий называются независимыми в совокупности, если любая комбинация из них независима.

О. 3. События называются зависимыми, если появление или не появление одного из них, изменяет вероятность появления другого.

О. 4. Вероятность события В, вычисленная в предположении осуществления события А, называется условной вероятностью события В и обозначается pA (B).

Пример 9. Из урны, содержащей 2 белых и 3 чёрных шара, наудачу последовательно извлекают два шара. Найти вероятность того, что второй извлечённый шар белый, если известно, что первый извлечённый шар чёрный.

Решение. Обозначим события А – первый извлечённый шар чёрный, В − второй извлечённый шар белый. Для нахождения искомой вероятности используем классическое определение

pA (B)= mn , где m- число благоприятных исходов, равное числу оставшихся после первого извлечения белых шаров, то есть m=2, а