Н.П.Курышкин Планы скоростей и ускорений

Министерство образования Российской Федерации

Кузбасский государственный технический университет

Кафедра прикладной механики

ПЛАНЫ СКОРОСТЕЙ И УСКОРЕНИЙ

Методические указания к практическому занятию по теории механизмов и машин для студентов направлений 552900, 551800, 551400

Составитель Н.П.Курышкин

Утверждены на заседании кафедры Протокол № 2 от 5 ноября 1999г.

Рекомендованы к печати учебно - методической комиссией направления 552900 Протокол № 237 от 15 ноября 1999г.

Электронная копия находится в библиотеке главного корпуса КузГТУ

Кемерово 2000

1

1. ЦЕЛЬ И СОДЕРЖАНИЕ ЗАНЯТИЯ

Цель занятия - практическое освоение методики кинематического анализа механизмов методом планов скоростей и ускорений.

Для предложенной схемы рычажного механизма по заданному движению входного звена необходимо определить скорости и ускорения всех шарнирных точек и центров масс звеньев. Требуется также определить угловые скорости и угловые ускорения всех звеньев.

2. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

Планы скоростей и ускорений представляют собой средство графического решения задачи о скоростях и ускорениях в механизме. Решение основано на разложении абсолютного движения какого-либо звена на некоторое переносное и относительное.

Переносным называется движение подвижной системы координат (ПСК) относительно неподвижной. ПСК искусственно вводится в механизм и связывается с каким-либо звеном или точкой звена, выбирается то звено или точка, движение которых (скорость и ускорение) уже известно. Относительным называется движение рассматриваемой точки (или звена) относительно ПСК. Переносное движение необходимо за-

давать таким, чтобы относительное движение звена, на котором лежит рассматриваемая точка, было простейшим - поступательным или вращательным.

Абсолютная скорость и ускорение при таком составном движении определяются по формулам:

vабс

=

vпе р+

vотн

,

(2.1)

a

=

a

+

a

+

a

,

абс

пе р

ко р

отн

где vпе р

и

a

пе р

- скорость и ускорение той точки ПСК, которая в дан-

ный момент совпадает с рассматриваемой;

vотн

и aотн

- скорость и ускорение рассматриваемой точки относи-

тельно ПСК;

a

ко р

- ускорение Кориолиса.

Графическое решение уравнений (2.1) называется планом скоростей и (или) планом ускорений соответственно. Напомним, что векторные уравнения разрешимы, если содержат не более двух неиз-

2

вестных. При этом надо учитывать не только модули, но и линии действия векторов.

Кинематический анализ механизмов ведется в порядке присоединения групп Ассура. Рассмотрим два примера.

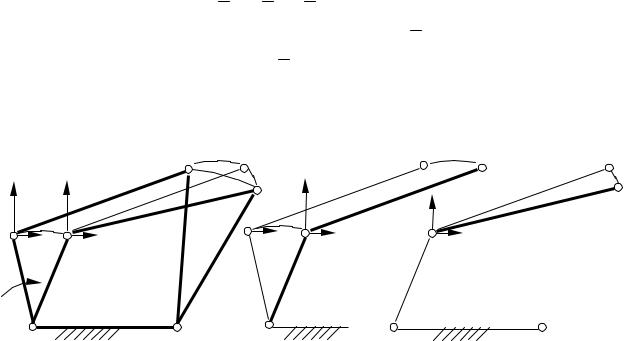
Пример 1. Дан шарнирный четырехзвенник с известной угловой скоростью и ускорением звена 1 (рис.1, а). Для изображенного положения требуется определить скорость и ускорение точек A и B.

По условию задачи следует, что звено 1 - начальное. Тогда цепь 2- 3 - первая и единственная группа Ассура. Скорости и ускорения точек внутри группы Ассура можно определить только в том случае, если известны скорости и ускорения мест присоединения группы в механизме. В нашем примере это точки А и С.

Скорость и ускорение точки A определяется непосредственно по

исходным данным:		=	ω 1 OA, м/с;
vA									(2.2)
anA		=	ω 12 OA, м/с2 ;						(2.3)
aτ		=	ε OA, м/с2 ;						(2.4)
A		=	1	n+
a	A		a		a	τ .			(2.5)
			A		A
Напомним, что нормальное ускорение							a	An	направлено к центру

вращения O, а			тангенциальное aAτ		- перпендикулярно OА и направлено
в сторону ε 1 .
	y	2	B	B′	y	B	B′	B′
y				B′′		y		B′′
A	x	A′ x	3	A x	A′ x	А′	x
1
O				C
		а)		б)			в)
	Рис. 1. К анализу движений в шарнирном четырехзвеннике
	Таким образом, скорости и				ускорения мест присоединения груп-

пы 2-3 известны (скорость и ускорение точки А только что найдены, а точки С - равны нулю). Для определения скорости и ускорения точ-

3

ки внутри группы Ассура - точки B - введем ПСК Axy, связав ее начало с точкой A и заставив двигаться поступательно. Представим, что абсолютное движение звена 2 (рис.1, а) складывается из поступательного переносного с системой Axy (рис.1, б) и вращательного относительно

Axy (рис.1, в).

В переносном движении точка B описывает траекторию BB', а в относительном - траекторию B'B". Так как переносное движение поступательное, то точка B в этом движении повторит траекторию точки A, и, следовательно, скорости и ускорения этих точек одинаковы.

На этом основании в формулах (2.1): vпе р = vA и aпе р = a A . Скорость и ускорение на траектории относительного движения В′В′′ обозначим как vВA и аВA . Тогда для нашего примера уравнения (2.1) будут иметь вид

vB		=	vA+		vBA ;				(2.6)
a	B	=	a	+	a	+	a	ко р .	(2.7)
			A		BA		BA

Решение этих уравнений не рассматриваем, т.к. в п. 3 будет разобран более общий случай.

Пример 2. Дан кулисный механизм (рис.2, а) с известной угловой скоростьюиускорениемкривошипа1. Определить скорость и ускорение точек А1, А2,

А3 .

A	2 x		A	x
y	A′′	y					A′′
1	A′	x		A′	x	y A′	x
	y			y
O
3

C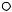

а) б) в)

Рис.2. К анализу движений в кулисном механизме

4

Как и в предыдущем примере, звено 1 - начальное, цепь 2-3 - группа Ассура. Скорость и ускорение шарнира А (точек А1 , А2 ) определяется поформулам(2.2), ..., (2.5). Скоростьиускорениеточки С равны нулю.

Требуется определить скорость и ускорение точки A3 . Эта точка неизменно связана со звеном 3 и совпадает в данный момент с шарниром А (рис.2, а).

Введем ПСК xy, которую свяжем с кулисным камнем 2. Абсолютное движение звена 3 представим состоящим из плоскопараллельного переносного с системой xy (рис.2, б) и прямолинейного поступательно-

го относительно xy (рис.2, в).			В переносном движении точка A3							опи-
сывает траекторию АА' (дугу			окружности с центром в точке О), а
в относительном движении -			траекторию А'А'' , параллельную звену
3. В абсолютном движении			точка				А3	описывает дугу окружности
АА'' с центром в точке С.
Из принятого разложения движения вытекают следующие форму-
лы скоростей и ускорений точки А3:
vA		=	vA		+	vA 2 ;				(2.8)
	3			2			3
a	A3	=	a	A2	+	a	+	a	ко р .	(2.9)
							A3 2		A3 2

Решение этих уравнений также не рассматриваем.

Во многих случаях для решения уравнений вида (2.1) одного разложения абсолютного движения оказывается недостаточно (это бывает тогда, когда число неизвестных больше двух). В этом случае используют еще одно разложение и получают систему двух векторных уравнений с четырьмя неизвестными, которая для групп Ассура всегда разрешима. Ниже в табл. 1 представлены все варианты двухповодковых групп Ассура и уравнения для определения скоростей и ускорений.

5

Таблица 1

Группы Ассура и векторные уравнения

№

Группа Ассура

Скорости

Ускорения

В

!

=

!

!

!

=

!

+

!

!

vB

vA+

vBA

a

a

a n+

a

τ

y

y

!

!

!

!B

!A

!BA

!BA

1

vB

=

vC+

vBC

a

=

a

+

a n +

a

τ

А

B

C

BC

BC

x

x

С

y3 3

x3

!

=

!

!

!

=

!

+

!

+

!

vC

vA+

vC A

a

C

a

a n

aτ

y

!

2

!

!

2

A

C A

C A

2

2

=

+

!

2

=

!

+

! 2

! 2

C

vC2

vC3

vC2 3

a

C2

a

a

+

a

ко р

A

C3

C2 3

C2 3

x

y

x

!

=

!

!

!

=

!

+

!

!

vB

vA+

vBA

a

a

a n+

a

τ

B

A

BA

BA

3

A

y4

!

=

!

+

!

!

=

!

+

!

+

!

ко р

B

vB

vB4

vB3 4

a

a

a

a

2

4

B

B4

B3

4

B3 4

x4

3

4

y4

!

=

!

+

!

!

!

!

!

y2

vA

vA

vA 2

a

=

a

+

a

+

a

ко р

4

2

3

!

3

! 2

!

3

!A3

!A2

!A3 2

!A3 2

vA3

=

vA4 +

vA3 4

a

=

a

+

a

+

a

ко р

А

x2

A3

A4

A3 4

A3 4

x4

y4

!

=

!

!

!

=

!

+

!

+

!

B x

1

vB

vB +

vB 1

a

2

a

1

a

a ко р

!

2

!

1

!

2

!

!

!

2

!

2

5

x4

4

vB2

= vB4 +

vB2 4

a

B2

= a

B4

+ a

+

a

ко р

y1

2

B2 4

B2 4

1

6

3. ПРИМЕР ПОСТРОЕНИЯ ПЛАНОВ СКОРОСТЕЙ И УСКОРЕНИЙ ПРИ ДВУХ РАЗЛОЖЕНИЯХ ДВИЖЕНИЯ

3.1. Условие задачи

Дано:

-кинематическая схема механизма (рис.3, а);

-координата ϕ 1 , угловая скорость ω 1 и угловое ускорение ε 1

звена 1.

Требуется определить скорости и ускорения точек А, С2, В, а также угловые скорости и ускорения звеньев.

3.2. Построение плана скоростей

Согласно изложенной выше методике, кинематический анализ будем вести от кривошипа 1 и далее в порядке присоединения групп Ассура. В нашем примере к начальному механизму, состоящему из стойки 0 и кривошипа 1, присоединена только одна двухповодковая группа Ассура, состоящая из кулисы 2 и кулисного камня 3 (см. строку 2 табл. 1). А2 и С3 - точки присоединения группы.

Скорость первой точки присоединения - точки А - определяется по

формуле (2.3), скорость второй - равна нулю.
Как следует из табл. 1, абсолютное движение	звена 2 разложе-
но дважды. Первый раз - на поступательное вместе	с системой коор-

динат Аху и вращательное относительно этой системы. Второй раз -

на плоскопараллельное вместе с системой x3 y3 (связанной со звеном

3) и

прямолинейное поступательноеотносительноэтой системы.

Скорость точки С2 определяется в результате решения систе-

мы векторных уравнений, взятых из табл. 1:

vC

2

=

vA

+

v

C A ,

(3.1)

2

2

ОA СА

vC2

=

vC3

+ vC2 3 ,

(3.2)

//AB

где

v

C A

- скорость точки С2 относительно системы Axy;

2

- скорость точки С2

относительно системы x3 y3.

vC 3

2

7

1

O 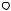ω 1 ε 1

0

		y		ко р
				aC2	3			p
		A		x
				ω	2
		2			vC2 3		c2
						b		a
				k
ω	2	=ω	3					б)

C			x3	b	c2		π
		3					n2
y3
					n1
	ε		= ε
В		2		3
						a
	a)						в)

Рис.3. Кулисный механизм - (а) с планом скоростей - (б) и ускорений - (в)

Переносные скорости vA		и vC определяются непосредственно по
	2	3
исходным данным: vA	= vA =	ω 1 lOA ,	vC = 0 .
2	1		3
Относительные скорости известны своими линиями действия.
Под векторами показаны линии их			действия. Кроме того, векторы

подчеркнуты двумя чертами, если они известны и по величине, и по направлению. Одна черта означает, что известна только линия действия. Это позволяет наглядно увидеть, что в системе четыре неизвестных: модуль и направление скорости vC2 , а также модули

относительных скоростей vC2 A , vC2 3 . При четырех неизвестных

система векторных уравнений разрешима. Для решения системы, из произвольной точки р (рис.3, б), называемой полюсом плана скоростей, проводим ра, изображающий скорость vA2 . Определяем масштабный

коэффициент будущего плана скоростей:

v = vА / pа, м с− 1 /мм.	(3.3)
2

8

Через масштабный коэффициент скорость любой точки определяется по формуле:

v = v v , м/c,	(3.4)
где v - выраженная в мм длина отрезка, изображающего	скорость

v на плане.

Далее, согласно уравнению (3.1), к построенному вектору прибавляем вектор vC2 A . Для этого из точки a перпендикулярно СА прово-

дим линию действия этого вектора.

Точно так же строим цепь векторов правой части уравнения (3.2). В точке пересечения линий действия относительных скоростей лежит конец вектора vC2 . Обозначим этот конец через с2. Искомые

vC2 , vC2 3 равны вектору рс2, а vC2 A - вектору ас2. Величины построен-

ных скоростей определяются по формуле (3.4). На этом система уравнений (3.1), (3.2) решена.

Скорость точки В кулисы 2 определим по теореме подобия, т.к. скорости двух точек (А и С2) этого звена уже известны. Согласно теореме подобия, точки одного и того же звена на схеме механизма и концы абсолютных скоростей (ускорений) этих же точек на плане скоростей (ускорений) образуютподобныеисходственно расположенныефигуры.

Исходя из теоремы, на отрезке ас2 (рис.3, б) построим треугольник ac2b, подобный треугольнику A С2 B (рис.3, а). Отрезок рb изобра-

жает искомую скорость.	Модуль скорости точки B найдем по форму-
ле(3.4).
На этом линейные скорости всех точек определены.		Найдем уг-
ловые скорости звеньев:
ω 2 =ω	3 = vC A / lAC , с-1.	(3.5)
	2

Направление угловыхскоростей определяетсянаправлениемвектора

vC2 A .

3.3. Построение плана ускорений

Нормальную и тангенциальную составляющие ускорения точки А определим по формулам (2.3), (2.4), а полное ускорение - их гра-

фическим сложением (рис. 3, в), где	π n	=	an	и	n а =	aτ	. Буквой
	1		А		1	А
π обозначен полюс плана ускорений.	Полное			ускорение			точки А:

9

аА =

π а a , м/с2,

где

а

- масштабный

коэффициент

плана

ускоре-

ний,

который

надо определить после выбора отрезка

π n1 .

Ускорение точки С2 определим из разложений движения, приня-

тых при определении скоростей ( см.

строку 2 табл. 1 ):

a

C2

=

а

А

+

а

n +

а

τ

,

(3.6)

С2 А

С2 А

//CA

CA

a

C2

=

a

+

a

+

a

ко р .

(3.7)

C3

C2 3

C2 3

=0

//АВ

АВ

Axy

Нормальное

ускорение

точки

C2

относительно системы

а

n

и ускорение

Кориолиса

а

ко р

подчеркнуты двумя

линиями,

т.

С2 А

С2 3

к. их модули известны.

Они определены по формулам:

аСn

А =

vC2

A

/ lAC ,

(3.8)

2

2

аСко 3р

=

2ω

пе р vотн =

2ω

3 vC 3 .

(3.9)

2

2

Направление

ускорения

Кориолиса получим поворотом вектора

относительной

скорости

vC 3

( рис. 3.1, б, в ) на 90o

в сторону

ω 3 .

2

Отметим, что

в уравнении

(3.6)

ускорение Кориолиса

а

ко р

отсут-

С2 А

ствует, т.к. угловая скорость системы Аху равна нулю (см. формулу

(3.9)).

Подчеркивания в системе векторных уравнений (3.6) и (3.7) показывают, что в ней четыре неизвестных. Значит она разрешима. Графическое решение этой системы не отличается от решения системы (3.1) и (3.2), поэтому ограничимся лишь указанием после-

довательности

откладывания векторов на плане ускорений

(рис. 3, в):

π а =

а

А

,

an

2

=

a n

, линия действия вектора

а

τ

. Затем,

C2 A

С2 А

π k =

aCко

3р ,

линия

действия вектора аС

3 . Заметим , что при построе-

2

2

нии цепочек

векторов

правой части уравнений (3.6) и

(3.7) сначала

откладывались

векторы известные по величине и направлению, а за-

тем проводились линии действия векторов, неизвестных по модулю.

Точку пересечения указанных линий действия обозначим

через c2. В

результате получим: a

C2

= π c

2

, a τ

=

n

2

c

2

,

а

С2 3

=

kc

2

. Модули

C2 А

искомых векторов определим по формуле:

a =

a

а ,

м/с2.