
- •Тема 1. Световые волны в прозрачной изотропной среде.
- •Тема 2. Поляризация света.
- •Тема 3. Излучение и поглощение света.
- •Тема 4. Отражение и преломление света.
- •Тема 6. Геометрическая оптика.
- •Тема 7. Спектр света.
- •Тема 8. Интерференция.
- •Тема 9. Дифракция.
- •Тема 10. Дифракционная решетка.
- •Тема 11. Голография.
- •Тема 12. Дифракционный предел разрешения.
- •Тема 13. Взаимодействие света с веществом.
- •Тема 14. Термодинамика излучения.
Санкт-Петербургский государственный университет
Физический факультет
Оптика
План-конспект лекций И. Р. Крылова
для студентов II курса
физического факультета,
обучающихся по направлению
"Прикладные математика и физика"
2005
На правах рукописи
Утверждено на заседании методической комиссии
Физического факультета СПбГУ
Составитель: доцент Крылов И.Р.
Рецензент:
План-конспект лекций представляет собой крайне сжатое изложение материла курса лекций по оптике. Отличие предлагаемого курса лекций состоит в попытке изложения "на пальцах" основных вопросов оптики. В лекциях, но не в план-конспекте, сделан упор на возможность понимания вопросов с минимальным использованием математического аппарата.
Тема 1. Световые волны в прозрачной изотропной среде.
Волновые уравнения для светового поля.
Уравнения Максвелла
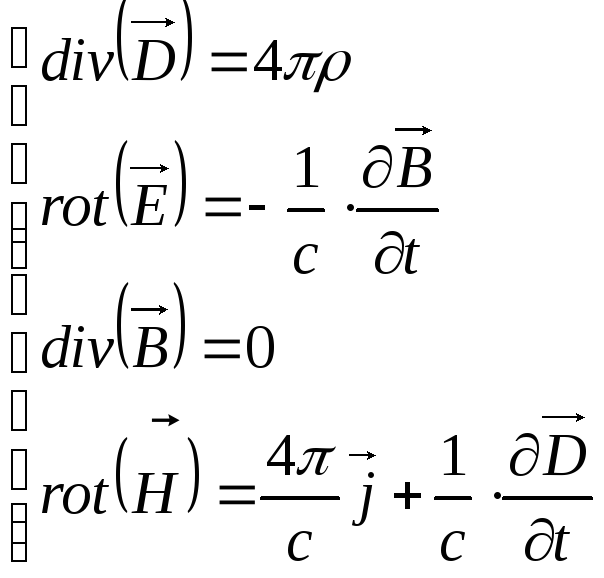 рассмотрим при условиях:
рассмотрим при условиях:![]() ,
,![]() ,
,![]() .
Из ротора второго уравнения с учетом
четвертого получим
.
Из ротора второго уравнения с учетом
четвертого получим![]() .
С другой стороны для любого векторного
поля
.
С другой стороны для любого векторного
поля![]() .
Откуда получаем волновое уравнение для
поля
.
Откуда получаем волновое уравнение для
поля![]()
![]()
где
![]() — скорость волны.
— скорость волны.![]() — определение показателя преломления
— определение показателя преломления![]() .
Следовательно
.
Следовательно![]() .
.
Факультативно. Частные решения волнового уравнения.
Разделение временной и пространственных
переменных решения волнового уравнения
![]() .
.
Пусть
![]() ,
подставим в волновое уравнение дляAи разделим уравнение наRT,
тогда одно слагаемое зависит только от
,
подставим в волновое уравнение дляAи разделим уравнение наRT,
тогда одно слагаемое зависит только от![]() ,
а другое — только отt.
Следовательно, каждое из двух слагаемых
равно константе, которую обозначим за
,
а другое — только отt.
Следовательно, каждое из двух слагаемых
равно константе, которую обозначим за![]() .
Тогда для функции координат получим
.
Тогда для функции координат получим![]() — уравнение Гельмгольца, а для функции
времени
— уравнение Гельмгольца, а для функции
времени![]() — уравнение гармонических колебаний,
где
— уравнение гармонических колебаний,
где![]() .
.
Разделение переменных решения уравнения
Гельмгольца в декартовых координатах,
пусть
![]() .
Подставим это решение в уравнение
Гельмгольца и разделим его на произведениеXYZ. При этом слагаемые
уравнения окажутся функциями разных
переменных и, следовательно, каждое
слагаемое — константа:
.
Подставим это решение в уравнение
Гельмгольца и разделим его на произведениеXYZ. При этом слагаемые
уравнения окажутся функциями разных
переменных и, следовательно, каждое
слагаемое — константа:![]() ,
,![]() ,
,![]() ,
где
,
где![]() .
Решения дляX,Y,Z— гармонические колебания
отx,y,z.
.
Решения дляX,Y,Z— гармонические колебания
отx,y,z.
Подставляя решения для X,Y,ZвR,
а затем решения дляRиTвA, получаем — решение
в комплексной форме в виде плоских волн![]() .
.
Разделение переменных в других системах
координат приводит к другим решениям.
Среди множества решений в цилиндрической
системе координат отметим решение в
виде цилиндрической волны
![]() ,
где
,
где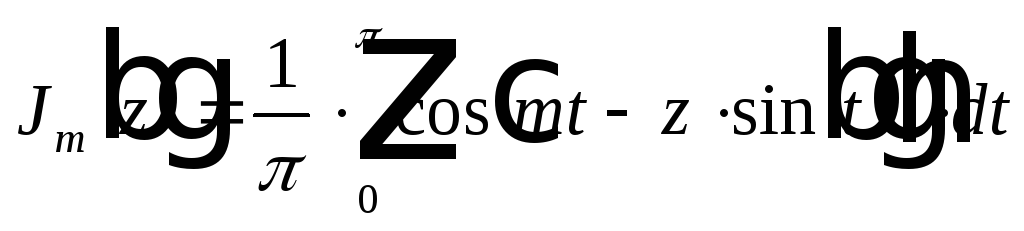 — функция Бесселя с целым значком
— функция Бесселя с целым значком![]()
Среди множества решений в сферической
системе координат отметим решение в
виде сферической волны ![]() .
.
Параметры плоской волны.
![]()
![]() — амплитуда волны,
— амплитуда волны,
![]() — начальная фаза волны,
— начальная фаза волны,
![]() — комплексная амплитуда волны,
— комплексная амплитуда волны,
T— период,![]() — частота,
— частота,![]() — циклическая частота волны,
— циклическая частота волны,
![]() — фазовая скорость волны,
— фазовая скорость волны,
λ — длина волны, k—
волновое число,![]() — волновой вектор,
— волновой вектор,
![]() ,
,![]() ,
,![]() — циклические пространственные частоты
волны,
— циклические пространственные частоты
волны,
![]() — фаза волны.
— фаза волны.
Фазовая скорость.
Рассмотрим плоскую волну, и направим
ось zвдоль вектора![]() .
Тогда
.
Тогда![]() ,
,![]() =>
=>![]() — фаза волны. Тогда
— фаза волны. Тогда![]() — уравнение постоянной фазы. Поскольку
в это уравнение входит в качестве
параметра времяt, то это
уравнение — уравнение движения
поверхности постоянной фазы, движения
фазовой поверхности.
— уравнение постоянной фазы. Поскольку
в это уравнение входит в качестве
параметра времяt, то это
уравнение — уравнение движения
поверхности постоянной фазы, движения
фазовой поверхности.
Продифференцируем это уравнение по
времени и получим
![]() откуда
откуда![]() ,
где
,
где
![]() — фазовая скорость волны.
— фазовая скорость волны.
Групповая скорость.
Рассмотрим две волны некоторой физической
переменной Aс разными,
но близкими частотами, бегущие вдоль
осиz![]()
![]() .
Введем обозначения
.
Введем обозначения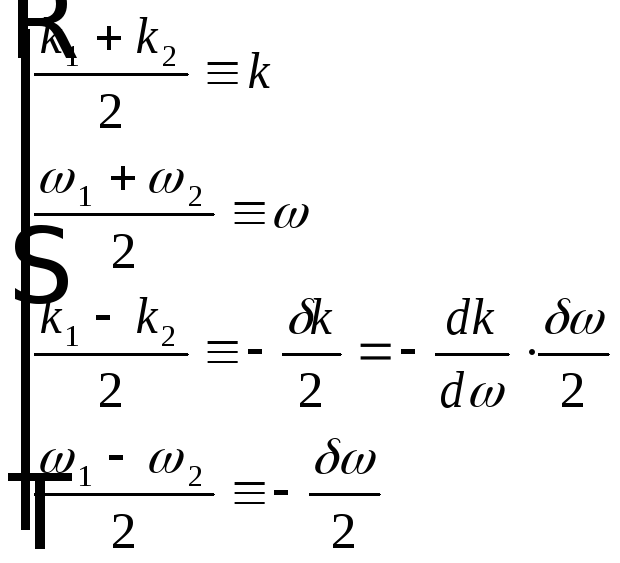 ,
тогда
,
тогда![]() ,
где
,
где![]() можно рассматривать, как медленно
меняющуюся амплитуду суммарной волны.
можно рассматривать, как медленно
меняющуюся амплитуду суммарной волны.
Для огибающей (или амплитуды) волны
уравнение постоянной фазы примет
следующий вид
![]() .
Дифференцируя это уравнение по времени,
получаем
.
Дифференцируя это уравнение по времени,
получаем![]() и, следовательно,
и, следовательно,![]() .
.
Окончательно,
![]() — групповая скорость волны, сравните
с фазовой скоростью волны
— групповая скорость волны, сравните
с фазовой скоростью волны![]() .
.
Поперечность световых волн.
Рассмотрим выражение для плоской волны
любой природы
![]() .
Продифференцируем его по времени и
получим
.
Продифференцируем его по времени и
получим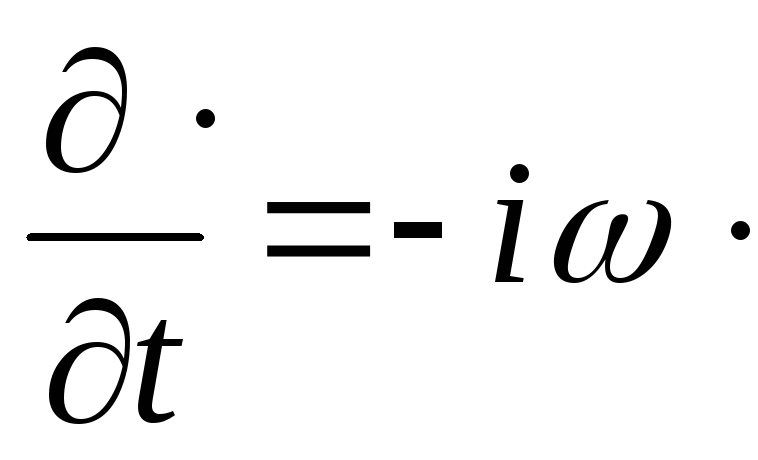 .
Аналогично, дифференцируя по
пространственным координатам, получим
.
Аналогично, дифференцируя по
пространственным координатам, получим![]() .
Подставим эти выражения в уравнения
Максвелла. Начнем с первого уравнения
.
Подставим эти выражения в уравнения
Максвелла. Начнем с первого уравнения![]() =>
=>![]() =>
=>![]() =>
=>![]() =>
=>![]() ,
но
,
но![]() ,
тогда
,
тогда![]() .
.
Аналогично получаем:
![]() ,
,![]() ,
,![]() ,
,![]() ,
где
,
где![]() — вектор Пойнтинга.
— вектор Пойнтинга.
Соотношение длин векторов E и H в бегущей световой волне.
![]() =>
=>![]() ,
но
,
но![]() ,
тогда
,
тогда![]() =>
=>![]() ,откуда
,откуда![]() в системе СГС Гаусса, или
в системе СГС Гаусса, или![]() в системе СИ.
в системе СИ.
Интенсивность света.
Интенсивность
![]() — плотность потока энергии (энергия в
единицу времени через единицу площади).
— плотность потока энергии (энергия в
единицу времени через единицу площади).
Связь интенсивности света с объемной плотностью энергии световой волны.
![]() ,
где
,
где![]() — фазовая скорость света, хотя казалось
бы, должна быть групповая.
— фазовая скорость света, хотя казалось
бы, должна быть групповая.
