FM_MMMFP (1) / Батаронов / ТИТУЛЬНИК МММ111готово

Содержание

Введение…………………………….………………………………………..4

1. Решение задачи №1…….…………………………………………….5

2. Решение задачи №2…….…………………………………………….8

Заключение……………………………….…………………………………11

Введение

В процессе диффузии искомой функцией является концентрация диффундирующего вещества, которую обычно обозначают через c = c(x, y, z, t). Функция c = c(x, y, z, t) удовлетворяет уравнению

.

Положительный коэффициент D называют коэффициентом диффузии. Начальное условие

задаёт начальную концентрацию. В качестве краевых условий рассматриваются главным образом условия

,

где Г – граница области, в которой происходит диффузия. Первое условие означает, что Г является непроницаемой для диффундирующего вещества стенкой, а второе условие задаёт концентрацию на границе Г [].

Уравнения параболического типа получается при исследовании таких физических явлений, как теплопроводность, диффузия, распространение электромагнитных полей в проводящих средах, движение вязкой жидкости.

Для решения задачи используется стандартное уравнение диффузии (параболического типа):

,

где U = U(x,y,t) – искомое распределение примеси, k – коэффициент диффузии, f – плотность источников или стоков поля, 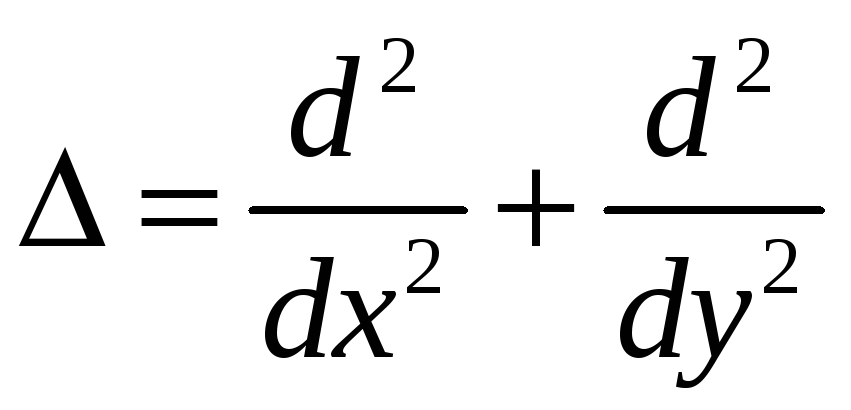- двухмерный оператор Лапласа в Декартовых координатах.

Решение задачи №1

Цилиндрический стержень, с заделанными концами, обрабатываемый в активной среде так, что диффузионный поток на поверхности стержня пропорционален разности концентрации U₀ и концентрации в стержне у поверхности. Найти распределение концентрации и уравнение для момента времени, когда минимальная концентрация стержня станет больше U₁ .

Решим данную задачу с помощью пакета FlexPDE :

title

"Float Zone"

coordinates

ycylinder('Z','R')

select

cubic { Use Cubic Basis }

variables

temp(threshold=100)

definitions

k = 0.85 {thermal conductivity}

cp = 1 { heat capacity }

long = 18

H = 0.8 {free convection boundary coupling}

Ta = 0 {ambient temperature}

A = 4500 {amplitude}

y=R

source = A*exp(-((z-1*t)/.5)**2)*(200/(t+199))

initial value

temp = Ta

equations

div(k*grad(temp)) + source = cp*dt(temp)

boundaries

region 1

start(0,0)

natural(temp) = 0 line to (0,1)

natural(temp) = 0 line to (long,1)

natural(temp) = -H*(temp - Ta ) line to (long,0 )

natural(temp) = 0 line to close

feature

start(0.01*long,0) line to (0.01*long,1)

time 0 to 18 by 0.01

monitors

for t = -0.5 by 0.5 to (long + 1)

elevation(temp) from (0,1) to (long,1) range=(0,1800) as "Surface Temp"

contour(temp)

plots

for t = -0.5 by 0.5 to (long + 1)

elevation(temp) from (0,0) to (long,0) range=(0,1800) as "Axis Temp"

histories

history(temp) at (0,0) (1,0) (2,0) (3,0) (4,0) (5,0) (6,0) (7,0) (8,0)

(9,0) (10,0) (11,0) (12,0) (13,0) (14,0) (15,0) (16,0)

(17,0) (18,0)

end 32936643

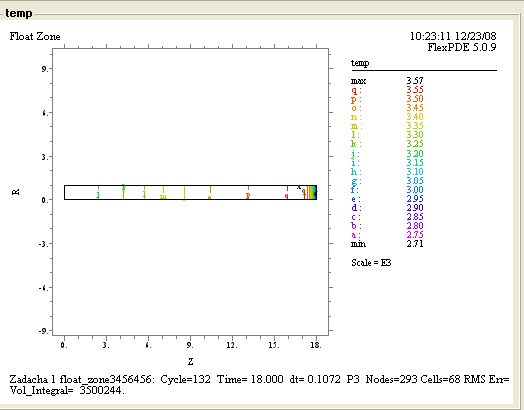
Рис.1 Распределение концентрации в цилиндре(диффузия).

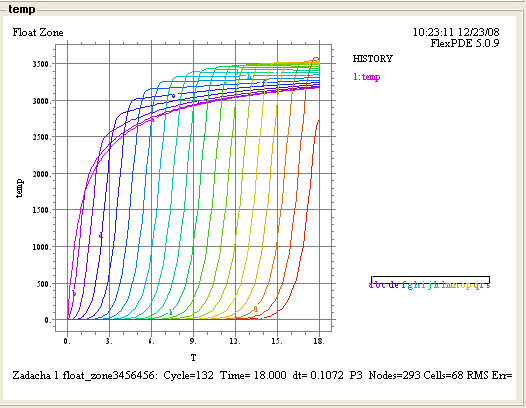
Рис.2 Изменение диффузионного потока.

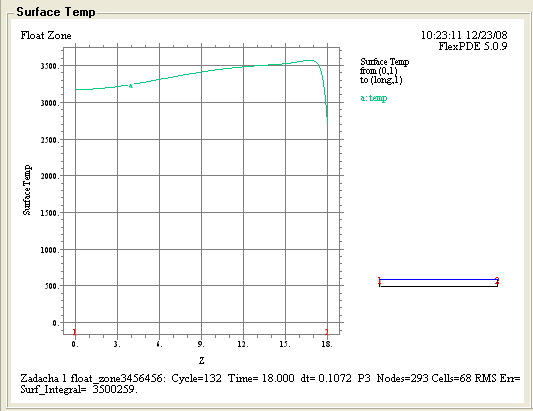
Рис.3 Изменение диффузии на поверхности.

Решение задачи №2

Две прилежащие стороны прямоугольной однородной пластинки покрыты тепловой изоляцией, а две другие поддерживаются при температуре равной нулю. Найти стационарное распределение температуры и её максимального значения при условии, что в пластинке выделяется тепло с плотностью Q=const.

Решим данную задачу с помощью пакета FlexPDE :

title "Coolant Pipe Heatflow"

select

stages = 3

errlim = staged(1e-3,1e-4,1e-5)

autostage=off

Variables

Temp { Identify "Temp" as the system variable }

definitions

K = 1 { define the conductivity }

source =9 { define the source }

flux = -K*grad(Temp) { define the thermal flux vector }

Initial values

Temp = 0 { unimportant in linear steady-state problems }

equations

div(K*grad(Temp)) + source = 0 { define the heatflow equation }

boundaries { define the problem domain }

Region 1 { ... only one region }

start "OUTER" (0,0) { start at the center }

natural(Temp)=0 { define the bottom symmetry boundary condition }

line to(0,10) { walk to the surface }

natural(Temp)=0 { define the "Zero Flow" boundary condition }

line to (10,10) { walk the outer arc }

value(Temp)=0 { define the Left symmetry B.C. }

line to (10,0) { return to close }

value(Temp)=0 { define the Left symmetry B.C. }

line to close { return to close }

monitors

contour(Temp) { show contour plots of solution in progress }

plots { write these hardcopy files at completion: }

grid(x,y) { show the final grid }

contour(Temp) { show the solution }

surface(Temp)

vector(-K*dx(Temp),-K*dy(Temp)) as "Heat Flow"

end 252506

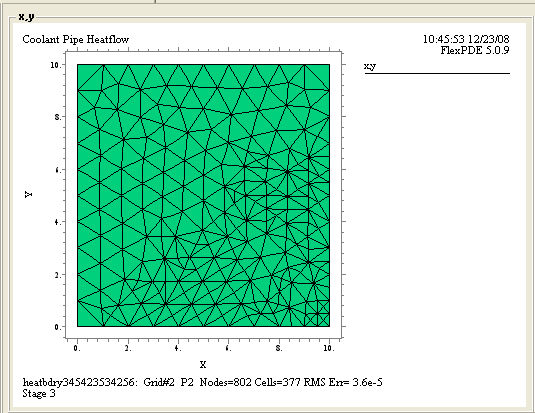
Рис.4 Распределение тепла по структуре.

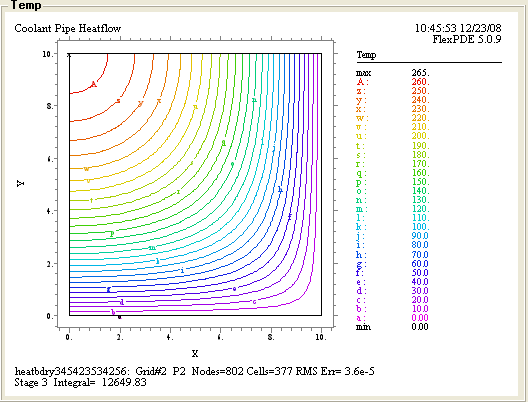
Рис.5 Распределение тепла.

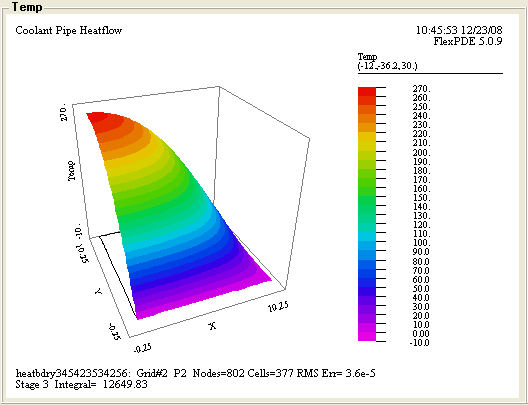
Рис.6 Перераспределение температур в объеме пластинки.

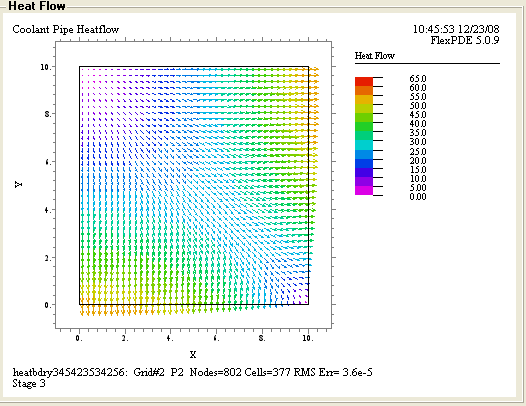
Рис.7 Направление распределения тепла.

Заключение.

В данной курсовой работе были проведено решение параболических задач методом конечных элементов с помощью FlexPDE. Были графически изображены распределения искомых величин (концентрации примеси, стационарное распределение температуры).

12