шпоры ответы на вопросы к экзамену по твимс

12. Локальная и интегральная теорема Муавра-Лапласа.

Локальная теорема Лапласа

12.

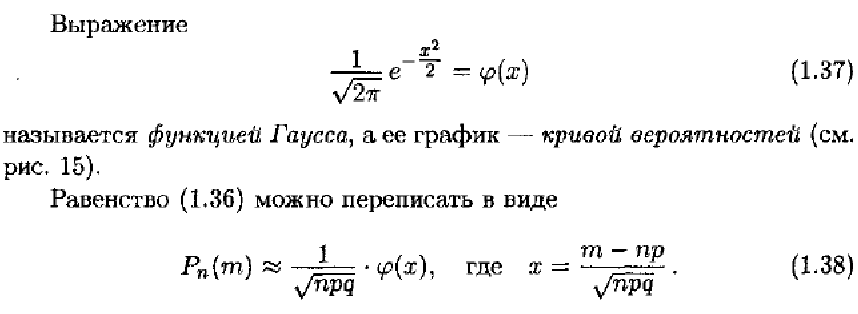
где

16. Плотность распределения и её свойства. Вероятностный и геометрический смысл плотности распределения.

16. Плотность распределения и её свойства. Вероятностный и геометрический смысл плотности распределения.

Используя получаем

18. Дисперсия и среднее квадратическое отклонение случайной величины. Свойства дисперсии. Производящая функция.

18.

19. Мода и медиана. Моменты случайных величин. Асимметрия и эксцесс. Квантили распределения.

19.

21. Непрерывная случайная величина. Числовые характеристики непрерывных случайных величин.

Определение 1: Величина X называется непрерывной случайной величиной, если вероятность попадания ее значения в любой интервал (x1,x2) может быть представлена в виде интеграла

             (7.6) от некоторой функции р(х) - плотности распределения вероятностей. При этом функция р(х) должна быть неотрицательной (что связано с неотрицательностью вероятностей) и должна быть нормирована условием

                           (7.7) отражающим достоверность события (сравни с (1) ). Если все возможные значения случайной величины X сосредоточены в конечном интервале (,), то считается, что вне этого интервала плотность р(х) = 0 и, значит, условие (7.7) сводится к условию

                             (7.8) Следует подчеркнуть, что для непрерывной случайной величины имеет смысл рассматривать только такое событие, как попадание в интервал, а не попадание в отдельную точку. Так как вероятность попадания непрерывной случайной величины в любую заранее заданную точку равна нулю.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Пусть непрерывная случайная величина Х задана плотностью распреде-

ления f(х). Допустим, что все возможные значения X принадлежат отрезку [а;b]. Разобьем этот отрезок на п частичных отрезков длиной Δx1 , 2 Δx , ..., n Δx и выберем в каждом из них произвольную точку i x ( i=1, 2, ..., п).

Определим математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений i x , на

вероятности попадания их в интервал i Δx :

21.

Перейдя к пределу, получим определенный интеграл

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а;b], называют определенный интеграл Если возможные значения принадлежат всей оси Ох, то Предполагается, что несобственный интеграл сходится абсолютно, т, е .существует интеграл Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к − ∞ , а верхнего - к + ∞ . По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения Х принадлежат отрезку [а;b], то если же возможные значения распределены по всей оси Ox, то

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:

27.

Def: математическим ожиданием составляющей  непрерывной двумерной случайной величины называют число:

, где 

В результате получим:

Математическим ожиданием составляющей  непрерывной двумерной случайной величины называют число:

Def: дисперсией составляющей  двумерной дискретной случайной величины называют число:

Дисперсией составляющей  двумерной дискретной случайной величины называют число:

Def: дисперсией составляющей  двумерной непрерывной случайной величины называют число:

 

дисперсией составляющей  двумерной непрерывной случайной величины называют число:

27. Зависимость и независимость двух случайных величин. Числовые характеристики двумерной с.в. Математическое ожидание и дисперсия.

Числовые характеристики двумерных случайных величин.

Def: математическим ожиданием составляющей  двумерной дискретной случайной величины называют число:

Математическим ожиданием составляющей  двумерной дискретной случайной величины называют число:

29. Предельные теоремы теории вероятностей. Неравенство и теория Чебышева

29.

34. Статистическое распределение выборки.

34. Статистическое распределение выборки.