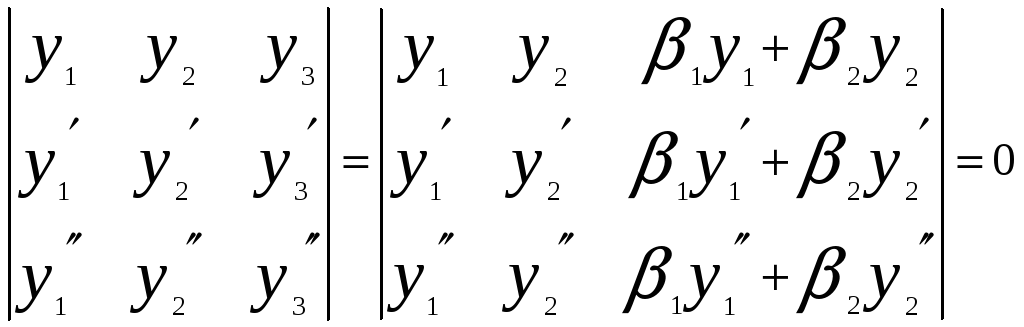1,2,31,34,19,20,15,16,13,14

1.Первообразная и неопределенный интеграл. Определение, свойства интеграла, таблица основных интегралов. Определение 1: Функция F(x) называется первообразной для функции f(x) в промежутке X если и Определение 2: Совокупность всех первообразных функций для данной функции f(x) в промежутке X называется неопределенным интегралом от функции f(x) и обозначается символом Основные свойства неопределенного интеграла: 1) 2) 3) Линейные свойства интеграла: 1) 2), где k – постоянная, (k не равно 0).

2. Непосредственное интегрирование. Теорема об инвариантности формул интегрирования. Подведение под знак дифференциала. Непосредственное интегрирование состоит в том, что заданный интеграл приводится к табличному путем тождественного преобразования подынтегральной функции и использовании линейных свойств интеграла. Теорема об инвариантности формул интегрирования. Вид формулы интегрирования не зависит от характера переменной интегрирования, т.е. если , а U= - любая дифференцируемая функция от x, то тогда . Доказательство: По условию теоремы, . Согласно свойству 2 неопределенного интеграла: =. Эта формула справедлива и в случае, когда аргументов функции F будет U= - любая дифференцируемая функция от x (свойство инвариантности дифференциала первого порядка): =. По свойству 3 неопределенного интеграла: К непосредственному интегрированию относят также подведение под знак дифференциала. По определение дифференциала функции: Преобразование по этой формуле называется подведением под знак дифференциала.

31.Векторное поле. Поток векторного поля через поверхность.Дивергенция.Теорема Остроградского-Гаусса(формулировка). Если в каждой точке M(x,y,z) области V определен вектор То говорят что в области V определено векторное поле. Оно определяется заданием одной векторной функции или заданием трех скалярных функций – координат этого вектора. Поток векторного поля Пусть в области V задано векторное поле: (S)-двусторонняя поверхность в области V. Фиксирована сторона поверхности,т.е указано напр. Нормали в какой либо ее точке. Пов-й инт. Второго рода называется потоком векторного поля через поверхность (S) в направлении нормали В.п. в виде П.И. первого рода cos,cos,cosy-это направляющие косинус нормали или координаты орта нормали . Поэтому Скалярное произведение векторов,которое запишем в виде Таким образом Дивергенция. Пусть -векторное поле в обл V,ф-и P,Q,R непрерывны в V вместе со своими 1-ми произв (S)-замкнутая по-ть в обл.V. Поток вект поля через внешнюю сторону пов (S) преобраз по форм острогор. Где V ‘-обл огр пов (S). Стоящее под знаком тр инт выраж наз дивергенцией Вект поля и обознач . Поток вект через вн стор замкнутой пов равен инт от диверг поля взятому по обл,огранич поверх S. Теор остр: Второе опр див-и:

34Комплексные числа. Комлексным числом Z наз. число z=x+iy, где x, y R. Мн-во комплексных чисел – С, R C, x–действ. часть, y – мнимая часть. Расстояние от z(x,y) до начала корд. наз. модулем комп. числа Z. Аргументом числа Z 0, наз угол , кот-й образует радиус-вектор точки Z и полож направл оси OX. Argz = argz (главное знач аргумента) + 2k kZ -<argz< argz = z = x+iy=zcos+izin=z(cos+isin) z=r(cos + isin) (!) z1 = r1(cos + isin) z2 = r2(cos + isin) тогда z1*z2 = r1*r2(cos(1+ 2) + isin(1+ 2) z^n= r^n(cos(n) + isin(n) - Формула Муавра (!) Формулы Эйлера: ; (!) ; ; ;

19.Линейные неоднородные дифф Ур-я. Теорема об общем решении.

20.Линейные неодн диф Ур с пост кооф. И спец видом правой части. Метод неопр кооф. Форма записи частн реш.

15.Уравнения, допускающие понижение порядка 1.уравнение вида (1) Порядок уравнения понижается путем последовательного интегрирования. Так как , то уравнение (1) можно переписать так: , откуда . Интегрируя еще раз, получим . Продолжая далее, после n интегрирований получим общее решение уравнения (1) 2. уравнение вида (2) не содержащие явно искомой функции у. Это позволяет понизить порядок уравнения при помощи подстановки . Тогда . Подставив выражения производных в уравнение (2), получим уравнение первого порядка относительно неизвестной функции р(х) проинтегрировав это уравнение, найдем его общее решение , а затем общее решение уравнения (2). Аналогично интегрируется уравнение вида Полагая , получим для определения р уравнение первого порядка , откуда , или . Это уравнение вида (1). 3. уравнения вида , (3) не содержащие явно независимой переменной х. понижение порядка в данном случае достигается подстановкой . В этом случае за независимую переменную принимается у. Тогда . Подставив в уравнение (3) выражения и , получим уравнение первого порядка относительно функции р(у): . Интегрируя это уравнение, найдем р как функцию от у и произвольной постоянной . Учитывая, что , получим уравнение первгого порядка для функции у от х: . Разделим переменные. Интегрируя это уравнение, получим общий интеграл исходного уравнения

16. Линейное однородное уравнение (f(x)=0) принимает вид (1) Если f(x) 0, то уравнение называется неоднородным. Для сокращения записи введем линейный дифференциальный оператор L(y) = Основные свойства оператора L(y): постоянный множитель можно выносить за знак оператора, т.е. L(Сy)=С L(y) оператор от суммы двух функций равен сумме операторов от этих функций Свойства частных решений линейного однородного уравнения Теорема 1: если функция есть решение линейного однородного уравнения, т.е. L()0, то функция , где С – произвольная постоянная, тоже является решением этого уравнения. Доказательство: по свойству однородности линейного оператора L()=С L(). Но, по условию теоремы, L()0, поэтому L()0, а это означает, что есть решение уравнения (1) Теорема 2: если функции и - решения уравнения (1), то их сумма у = +тоже является решением уравнения (1) Доказательство: по свойству аддитивности оператора = L()+. По условию теоремы L()0, 0. Поэтому 0, т.е. функция + - решение уравнения (1) Теорема 3: если функция , ,… - решения уравнения (1), то их линейная комбинация у = ++…+, где ,,…,- произвольные постоянные, тоже являющиеся решением уравнения (1) Доказательство: по теореме 1 каждая из функций ,,…, является решением уравнения (1) По теореме 2 функции =+ - решение уравнения (1) и т.д. Набор чисел ,,…,будем называть тривиальным, если эти числа равны нулю ==…==0 Набор чисел будем называть нетривиальным ,,…,, если хотя бы одно из этих чисел 0, Определение1: функции , ,… называются линейно зависимыми на интервале (a,b), если существует их нетривиальная линейная комбинация, равная нулю для всех , т.е. ++…+=0 , если 0, Определение2: функции , ,… называются линейно независимыми на интервале (a,b), если только их тривиальная линейная комбинация равна нулю для всех , т.е. ++…+=0 0 , Для случая двух функций иих линейная независимость на интервале

сводится к тому, чтобы соотношение этих функций не было постоянным на интервале , при этом имеется в виду, что это соотношение определено во всех точках интервала . Если одна из функций , ,… тождественно равна нулю на интервале , то эти функции линейно зависимы на . Пусть, например, 0, . Тогда при любом и при будет выполняться соотношение ++…+=0 Это означает, что функции , ,… линейно зависимы на интервале . Необходимое условие линейной зависимости n функций Пусть функции , ,…имеют производные порядка n-1. Определитель n-го порядка w(x) = называется определителем Вронского для функций , ,…или вронскианом этих функций. Теорема: если функции , ,…линейно зависимы на интервале , то их вронскиан w(x) тождественно равен нулю на этом интервале Доказательство: проведем док-во для случая n=3. пусть функции , ,линейо зависимы на интервале , т.е. мы имеем равенство ++=0 (2) , где не все равны нулю. Пусть например, . Разрешим равенство (2) относительно (3), где , Продифференцируем это тождество 2 раза и подставим согласно (3) и найденные отсюда производные и в последний столбец определителя вронского w(x) = Последний определитель равен нулю, так как его третий столбец является линейной комбинацией первых двух столбцов. Доказанное необходимое условие линейной зависимости n функций , ,…не является достаточным