Энергия заряженного конденсатора

Энергию W заряженного конденсатора найдем, умножив w из (5.13) на объем конденсатора V = Sd. Выразив, в соответствии с (3.22), напряженность электрического поля Е через разность потенциалов (напряжение) U, получим:

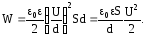
С учетом формулы емкости плоского конденсатора (5.5) для энергии заряженного до напряжения U конденсатора емкостью С имеем следующее выражение:

(5.15)

Формула (5.15) верна для конденсаторов любой формы, хотя получили мы ее для частного случая плоского конденсатора.

13. Теорема Гаусса в интегральной и дифференциальной форме

Вычислим поток вектора напряженности электрического поля через замкнутую поверхность. Первоначально будем считать, что поверхность – сфера, а в центре ее находится точечный заряд q. Напряженность электрического поля точечного заряда определяется выражением . Вектор нормали к сферической поверхности совпадает с направлением радиуса сферы, поэтому в данном случае поток равен:

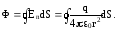
Потоком вектора напряженности электрического поля называют интеграл по поверхности от скалярного произведения векторов иdS.

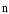(1)

Элементарный поток вектора напряженности электростатического поля

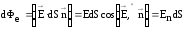, (2)

где Е_n  проекция вектора 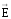на нормаль.

Рис. 2.2

Ф = 0, если внутри замкнутой поверхности заряд q = 0.

теорема Гаусса: поток вектора напряженности электрического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри поверхности, деленной на 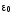– электрическую постоянную.

Таким образом, при V 0 в формуле (8) его левая часть стремится к diV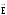, а правая  к .

Следовательно, 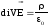. (10)

Формула (10) выражает теорему Гаусса в дифференциальной форме.

Запись формул и действия с ними упрощаются при введении векторного дифференциального оператора

, (11)

где  единичные векторы осей Х, У, Z соответственно.

Векторный дифференциальный оператор 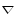приобретает вполне определенный смысл только в сочетании со скалярной или векторной функцией, на которую символически умножается, т. е. теорему Гаусса в дифференциальной форме

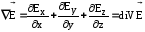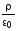=(12)

Теорема Гаусса является локальной, т. е. дивергенция поля 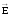в заданной точке этого поля зависит только от объемной плотности электрического заряда.

14. Применение теоремы Гаусса. Электрическое поле равномерно заряженной плоскости. Уравнения Пуассона и Лапласа Поле бесконечной равномерно заряженной плоскости

. Электрическое поле равномерно заряженной плоскости

Пусть бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда +.

Рис. 3

Из свойств симметрии заряженной плоскости следует, что вектор напряженности электрического поля, созданного этой плоскостью, всюду перпендикулярен ей.

В симметричных точках этого поля вектор равен по модулю и противоположен по направлению. В связи с этим в качестве замкнутой поверхности можно выбрать цилиндрическую (рис. 3). Полный поток вектора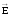пронизывающий

Ф_е = 2ЕS.

Согласно теореме Гаусса

,

где

.

Таким образом,

или

, (13)

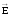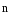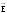
где Е_n  проекция вектора на нормаль(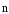, рис. 3).

Если   0, то Е_n  0, т. е. вектор 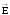направлен от заряженной плоскости (линии напряженности начинаются на положительных зарядах).

Если   0, то Е_n  0, т. е. вектор форме направлен к заряженной плоскости (линии напряженности оканчиваются на отрицательных зарядах).

Согласно (13) напряженность электростатического поля, созданного равномерно заряженной бесконечной плоскостью, не зависит от расстояния до нее, а поле является однородным справа и слева от плоскости.