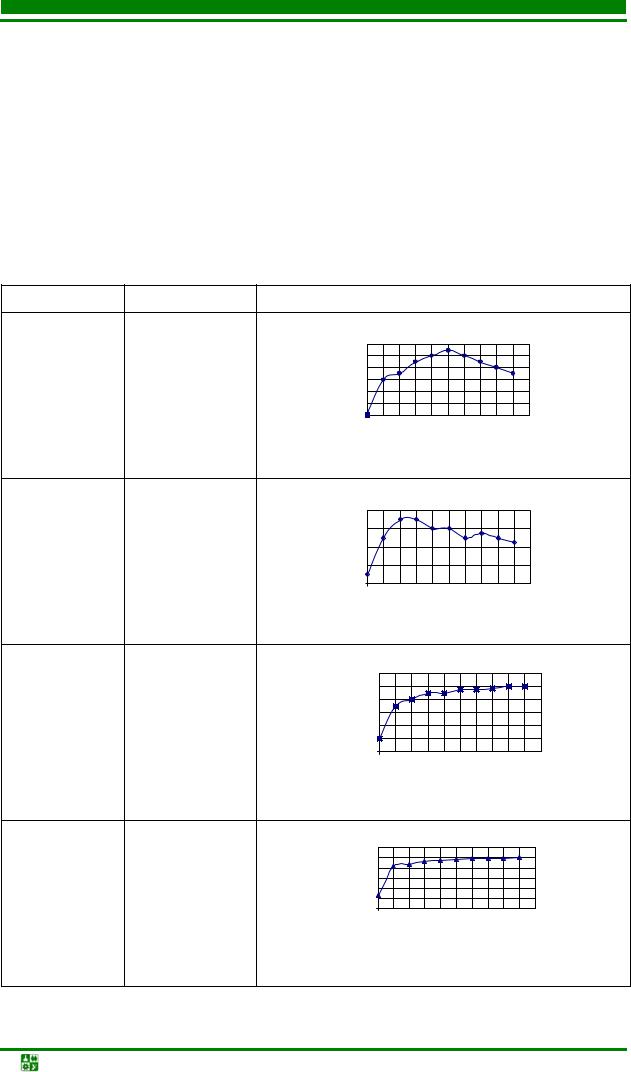
ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Задание

Варианты 1–9

Определить зависимость предела прочности сплава (варианты 1–3), предела текучести (варианты 4–6) или относительного удлинения (варианты 7–9) сплава В95 от времени искусственного старения, используя данные табл. 1.1.

Таблица 1.1

Номер варианта	Температура, оС
1	120

2

135

3

150

4

135

График

	2	60
	кг/мм
		58
	,	56
	прочности
		54
		52
		50
	Предел
		48
		0	4	8	12	16	20	24	28	32	36	40
						Старение, ч

2	56
кг/мм
	54
прочности,
	52
Предел	50
	48
	0	4	8	12	16	20	24	28	32	36	40

Старение, ч

2	58
кг/мм
	56
прочности,	54
	52
	50
	48
Предел
	46
	0	4	8	12	16	20	24	28	32	36	40
					Старение, ч

2
мм	60
кг/	50
,
текучести	40
	30
	20
Предел	10
	0
	0	4	8	12	16	20	24	28	32	36	40
					Старение, ч

Моделирование процессов и объектов в металлургии. Лаб. практикум

-20-

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

		Задание
							Продолжение табл. 1.1
Номер варианта	Температура, оС					График
		2
		мм	60
		кг/	50
		текучести,
			20
			40
5	120		30
		Предел	10
			0
			0	4	8	12	16	20	24	28	32	36	40
							Старение, ч
		2	60
		кг/мм
			50
		,	20
		текучести
			40
			30
6	150	Предел	10
			0
			0	4	8	12	16	20	24	28	32	36	40
							Старение, ч

			25
7	150	Относительн. удлинение,%	20
			5
			15
			10
			0
			0	4	8	12	16	20	24	28	32	36	40
							Старение, ч
		удлинение,%	20
			16
			12
		.	8
8	135	Относительн	0	0	4	8	12	16	20	24	28	32	36	40
			4
								Старение, ч

		удлинение,%	25
			20
			15
9	120	Относительн.	10
			0	4	8	12	16	20	24	28	32	36	40
			5
			0
							Старение, ч

Моделирование процессов и объектов в металлургии. Лаб. практикум

-21-

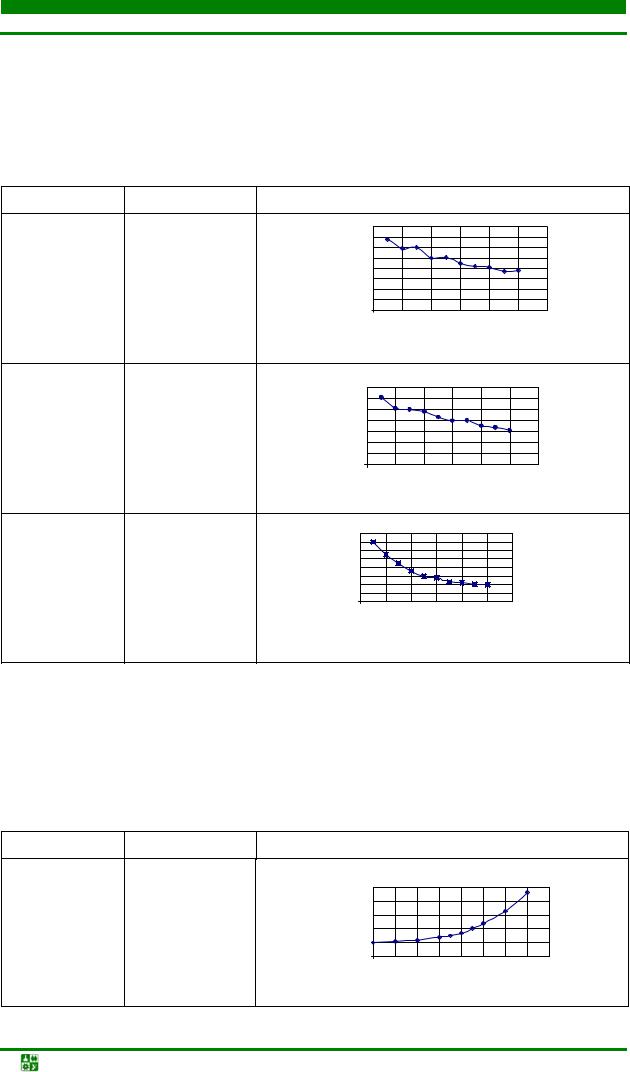
ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Задание

Вариант 10–12

Определить зависимость изменения глубины диффузионного слоя ниобия при нагреве в течение 1 ч на воздухе до указанной температуры (табл. 1.2).

Номер варианта	Температура, оС
10	1 200

11

1 000

12

800

Таблица 1.2

График

	2	800
	/мм	700
	, кг
		600
	Микротвердость
		100
		500

400

300

200

0

0

0,08

0,16

0,24

0,32

0,4

0,48

Расстояние от поверхности, мм

	2	700
	мм	600
	кг/
		500
	Микротвердость,
		400
		300
		200

100

0

0

0,08

0,16

0,24

0,32

0,4

0,48

Расстояние от поверхности, мм

2	800
мм	700
кг/	600
Микротвердость,	500
	400
	300
	200
	100
	0
	0	0,08	0,16	0,24	0,32	0,4	0,48
		Расстояние от поверхности, мм

Вариант 13–16

Для кремнистых бронз определить зависимость указанного параметра от содержания кремния (табл. 1.3).

Таблица 1.3

Номер варианта	Параметр				График
			250
		2
		мм	200
		кг/	150
13	Твердость	Твердость,
			50
			100
			0
			0	1	2	3	4	5	6	7	8
						Содержание Si, %

Моделирование процессов и объектов в металлургии. Лаб. практикум

-22-

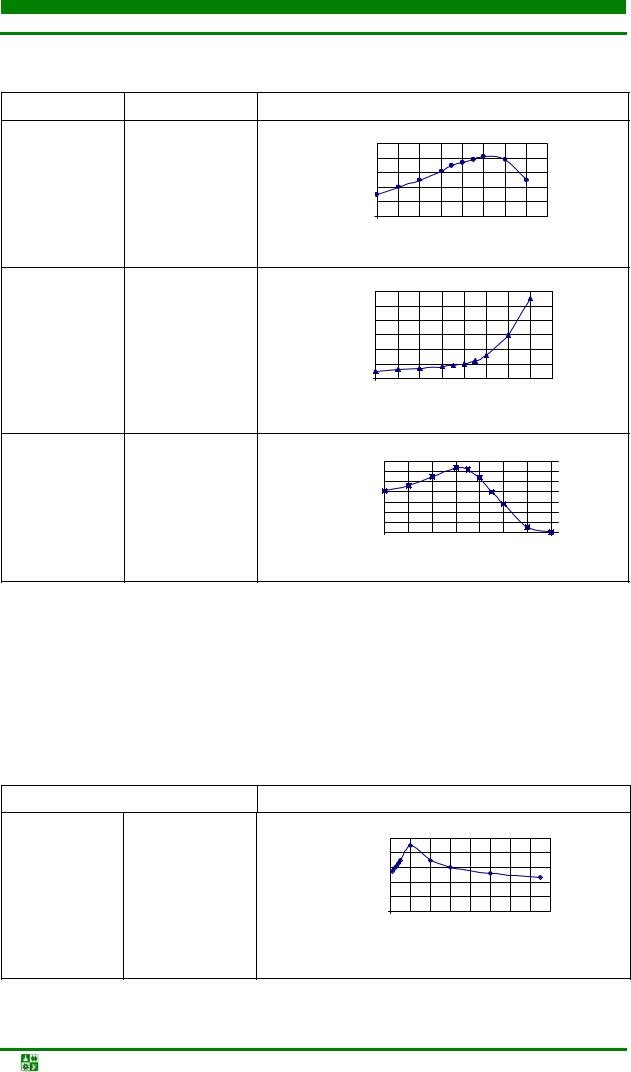
ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Задание

Продолжение табл. 1.3

Номер варианта

Параметр

	14	Предел
		прочности

15Предел

текучести

16Относительное

удлинение

График

2	50
кг/мм
	40
прочности
	30
	20
Предел	10
	0
	0	1	2	3	4	5	6	7	8

Содержание Si, %

2	60
/мм	50
кг
текучести,	40
	30
Предел	20
	10
	0
	0	1	2	3	4	5	6	7	8

Содержание Si, %

Относительн.удлинение,%	70
	60
	50
	40
	30
	20
	10
	0
	0	1	2	3	4	5	6	7
				Содержание Si, %

Вариант 17–20

Для сплавов цинка определить зависимость указанного параметра от естественного старения (табл. 1.4).

Номер варианта	Параметр

17 Твердость

Таблица 1.4

График

	2	100
	/мм	80
	кг	60
	Твердость,
		40
		20
		0

0

10

20

30

40

50

60

70

80

Время выдержки, мин

Моделирование процессов и объектов в металлургии. Лаб. практикум

-23-

ЛАБ. Р. 1. ОПР-Е ПАРАМЕТРОВ РЕГРЕСС. МОДЕЛИ ПО ЭКСПЕРИМЕНТ-М ДАННЫМ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Задание

Номер варианта	Параметр

18Температура

19Электросопротивление

	20	Изменение
		длины

Продолжение табл. 1.4

График

	60
0	50
С
,	10
Температура
	40

30

20

0

0

10

20

30

40

50

60

70

80

Время выдержки, мин

	2
	х10	14
	Ом	12
	Электросопротивление,	10
		8
		6
		4
		2
		0
		0	10	20	30	40	50	60	70	80
					Времявыдержки, мин

длины,%	0,35
	0,3
	0,25
	0,2
Изменение
	0,15
	0,1
	0,05
	0
	0	10	20	30	40	50	60	70	80
				Время выдержки, мин

Контрольныевопросыизадания

1.Дайте определения математической модели и объекта.

2.В чем заключается задача регрессионного анализа?

3.Какую величину называют случайной? Опишите основные типы случайных величин.

4.Сформулируйте закон распределения случайной величины.

5.Назовите виды регрессионных зависимостей.

6.Какая характеристика служит для оценки качества линейной модели? Какие она может принимать значения?

7.Описать сущность МНК.

8.Какая характеристика служит для оценки качества нелинейной модели? Какие она может принимать значения?

9.Дайте определение корреляции. Какие виды корреляции вы знаете?

10.Можно ли считать, что математическая модель и линия регрессии одно и то же? Как строится линия регрессии?

11.Опишите метод построения гистограммы.

12.В чем заключается содержательный анализ остатков модели?

13.В каких случаях используется корреляционный коэффициент, а в каких – корреляционное отношение как критерий адекватности модели?

14.Назовите этапы построения и исследования регрессионной моде-

ли.

15.Каковы методы проверки адекватности структуры модели?

Моделирование процессов и объектов в металлургии. Лаб. практикум

-24-

ЛАБОРАТОРНАЯ РАБОТА 2

МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Цельработы

Ознакомиться с методами оптимизации и численными алгоритмами для решения задач безусловной оптимизации; научиться решать задачи безусловной оптимизации с использованием пакетов прикладных программ на ЭВМ; научиться анализировать полученные результаты.

Краткиетеоретическиесведения

Решение всякой задачи оптимизации начинается с ее математической постановки.

Постановказадачибезусловнойоптимизации

Общая постановка задачи состоит в следующем. Задано: множество X и функция f(x), определённая на Х.

Требуется: найти точки минимума или максимума функции f на X. Будем записывать задачу на минимум в виде

f(x) → min, х X.

(2.1)

Задача (2.1) сформулирована как задача нахождения минимума функции f(x), или минимизации f(x). На практике же приходится сталкиваться как с задачами минимизации, так и с задачами максимизации f(x), т.е. нахождения точек максимума f(x):

f(x) → max, х Х.

С математической точки зрения различия между задачами минимизации и максимизации не существенны, поскольку максимизация f(x) эквивалентна минимизации функции −f(x). Поэтому всегда можно ставить задачу оптимизации как задачу минимизации (2.1).

Функция f(x) в выражении (2.1), т.е. функция, которую мы минимизируем, называется целевой. Множество Х в формуле (2.1), на котором мы минимизируем f(x), называется допустимым множеством задачи, а любой элемент х Х − допустимой точкой задачи. Допустимая точка х* Х, в которой

Моделирование процессов и объектов в металлургии. Лаб. практикум

-25-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения

целевая функция f(x) достигает своего минимума, называется решением задачи.

Следует иметь в виду, что на практике допустимая точка х может представлять собой некоторый набор параметров х = (х1, ..., хn). Причём значения этих параметров могут подчиняться ограничениям или изменяться без ограничений. Если, например, хi выражает количество производимого продукта i-го вида (сплав соответствующей марки и пр.) для каждого i = 1, ..., n, то при этом будет существовать ограничение на производственную мощность (например, 0 ≤ хi ≤ аi, i = 1, ..., n) и ограничение на количество товара, которое может поглотить рынок (например, α1х1 + α2х2 + … + αnхn ≤ b, где αi

– рыночная цена i-го товара; b – общая денежная масса).

Необходимо подчеркнуть, что само понятие точки минимума (решения задачи (2.1)) неоднозначно и требует уточнения.

Точка х* Х называется точкой глобального минимума функции f(x) на множестве Х или глобальным решением задачи (2.1), если

f(x*) ≤ f(x) при всех х Х.

(2.2)

Точка х* Х называется точкой локального минимума f на Х или локальным решением задачи (2.1), если существует такое подмножество Uδ

(х*) = {x x X, || x − x*|| ≤ δ}, что
	f(x*) ≤ f(x) при всех x Uδ(x*).						(2.3)
Здесь и далее
	x − x *				= ∑n (xi − xi )2 1/ 2 .
					i=1

Очевидно, что глобальное решение является и локальным, обратное неверно.

Для отражения того факта, что точка x* X является точкой глобального минимума функции f на X, будем использовать запись

f (x ) = min f (x).

x X

Если неравенство в (2.2) или (2.3) выполняется как строгое при x ≠ x*, т.е. f(x) < f(x*), x X (или x Uδ(x*)), то говорят, что x* – точка строгого минимума (строгое решение).

При изучении задач оптимизации в первую очередь возникает вопрос о существовании решения. Условия, гарантирующие разрешимость задачи (2.1), содержатся в следующей теореме из курса высшей математики [1, 2, 4].

Моделирование процессов и объектов в металлургии. Лаб. практикум

-26-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения

Т е о р е м а 1 (Вейерштрасса). Пусть Х – ограниченное замкнутое множество в Rn, f(х) – непрерывная функция на Х. Тогда существуют точки глобального минимума и максимума функции f на Х (глобальное решение за-

дачи (2.1)).

Эта теорема отвечает на вопрос о существовании решения, но не даёт конструктивного алгоритма нахождения этого решения. Следует также учесть, что задача оптимизации может иметь несколько решений. Вопрос о единственности решения рассматривается отдельно для каждого класса задач (классификациюзадачоптимизацииможнонайти, например, вучебнойлитературе[1, 2]).

При изучении любого типа задач оптимизации важное место занимает вопрос об условиях оптимальности, или, как еще говорят, условиях экстремума. Различают необходимые условия оптимальности, т.е. условия, которым должна удовлетворять точка, являющаяся решением задачи, и достаточные условия оптимальности, т.е. условия, из которых следует, что данная точка является решением задачи. В общем случае суть всех критериев оптимальности для задачи (2.1) заключается в том, что из точки х*, являющейся локальным решением, нельзя осуществить сколь угодно малый сдвиг в каком бы то ни было направлении, приводящий к уменьшению значения целевой функции, и остаться при этом в пределах допустимого множества.

Постановказадачибезусловнойоптимизации

Если допустимое множество Х = Rn, то задача (2.1) называется задачей безусловной оптимизации. Приведем ее математическую постановку.

Задано: функция f(х), определенная на Rn.

Требуется: найти точки минимума функции f на Rn. Иначе говоря,

f(х) → min, х Rn.

(2.4)

Теория необходимых и достаточных условий оптимальности в задачах безусловнойоптимизацииизлагаетсявлюбомкурсевысшейматематики[2, 3].

Необходимое условие оптимальности. Пусть функция f дифференци-

руема в точке х* Rn. Если х* – локальное решение задачи (2.4), то все первые производные функции f в точке х* равны нулю:

∂f	(x )= 0,	i =1, 2, …, n.
∂x
i

Достаточное условие безусловного локального минимума связано со вторыми производными функции f. При n = 2 наличие экстремума в точке х* зависит от знака определителя

Моделирование процессов и объектов в металлургии. Лаб. практикум

-27-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения

		∂2 f	(x *)
		∂x2
D =		1
		∂2 f		(x *)
		∂x ∂x
		1	2

∂2 f			(x *)
∂x ∂x
1	2			.
∂2 f
		(x *)
∂x2
2

Пусть функция f дважды дифференцируема в точке х* Rn и первые частные производные (градиент) функции f в точке х* равны нулю. Тогда функция f достигает экстремума в точке x* при D > 0. Причем, если

∂2 f (x *)> 0,

∂x12

то х* − точка локального минимума. Если

∂2 f (x *)< 0,

∂x12

то х* − точка локального максимума.

Для функции f числового аргумента (n = 1) достаточные условия экстремума означают, что если f′(x*) = 0 и f′′ (x*) > 0, то x* − решение задачи (2.4).

Методыодномернойбезусловнойминимизации

Изучение методов безусловной оптимизации начинается с наиболее простого типа оптимизационных задач, в которых целевая функция зависит от одной переменной.

Поскольку универсальных методов, пригодных для минимизации любых функций одной переменной, не существует, приходится строить алгоритмы, ориентированные на различные классы функций, встречающиеся в прикладных задачах.

Рассмотрим методы одномерной минимизации так называемых унимодальных функций.

Функция f называется унимодальной на Х, если существует такая точка х* Х, что для любых x1, x2 X

f(x1) > f(x2), если х1 < x2 < x*, f(x1) < f(x2), если х* < x1 < x2.

Для непрерывных функций свойство унимодальности означает наличие у неё единственного локального минимума. Предположение об унимо-

Моделирование процессов и объектов в металлургии. Лаб. практикум

-28-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения

дальности целевой функции не является жестким ограничением и выполняется во многих практических задачах поиска оптимума.

Если известен какой-либо отрезок [хk, хm], которому принадлежит х*, будем говорить, что точка минимума х* локализована в отрезке [хk, хm]. Сам отрезок при этом будем называть отрезком локализации минимума. В лите-

ратуре интервал (хk, хm) называется интервалом неопределённости.

Все методы минимизации унимодальных функций опираются на следующее утверждение.

Т е о р е м а 2. Пусть функция f унимодальна на Х и х1 < x2. Тогда, ес-

ли f(x1) ≤ f(x2), то х* ≤ х2, если же f(x1) ≥ f(x2), то х* ≥ х1, а если f(x1) = f(x2), то

х* [х1, х2].

Работа любого алгоритма минимизации состоит из двух этапов. На первом этапе вычисляются предусмотренные алгоритмом характеристики задачи. На втором этапе по полученной информации строится приближение к решению. Обычно для задания алгоритма достаточно указать способ выбора точек приближения xk = (х1k, …, хnk) Χ, k =1, 2, … Выбор точек приближения называется поиском точек.

Если все точки выбираются одновременно до начала вычислений, то алгоритм минимизации называется пассивным. Однако для решения большинства задач точки приближения выбираются поочередно, т.е. точка х(k+1) выбирается тогда, когда уже выбраны точки предыдущих вычислений х(1), х(2), …, х(k) и в каждой из них произведены предусмотренные алгоритмом вычисления. Такие алгоритмы называются последовательными.

К последовательным методам поиска экстремума унимодальных функций одной переменной относятся методы исключения интервалов, включающие методы дихотомии, Фибоначчи, золотого сечения. Простейшим из них является метод дихотомии. Его суть состоит в следующем.

Пусть количество допустимых вычислений функции N = 2k. При-

мем x	= a +b	−δ,	x	= a +b	+ δ, где δ – некоторое положительное число,
1	2		2	2

δ < (a + b)/2k. Вычислим f(x1) и f(x2) и определим новый отрезок локализации

минимума. Согласно теореме 2, если f(x1) < f(x2), то х* [а, х2]; если f(x1) > f(x2), то х* [x1, b]; если f(x1) = f(x2), то х* [x1, x2]. В превом случае искомым от-

резком будет [a, x2], во втором − [x1, b], в третьем − [x1, x2].

Для единообразия в случае f(x1) = f(x2) будем рассматривать в качестве нового отрезка локализации минимума, например, [a, x2]. Так что длина от-

резка локализации после первой пары вычислений функции равна b−2a +δ.

Вторая пара значений f вычисляется в точках х3, х4, отстоящих на расстоянии δ по обе стороны от середины нового отрезка локализации. Если, например, этим отрезком оказался [a, x2], то

x =	a + x2	− δ,	x	4	=	a + x2	+ δ.
3	2				2

Моделирование процессов и объектов в металлургии. Лаб. практикум

-29-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения

Используя снова те же условия, определяем новый отрезок локализа-

ции минимума длиной b−4 a + 32δ.

После N вычислений функции мы нашли отрезок локализации минимума [xN-1, xN] длиной

	l =	b − a	+	2N / 2 −1		δ,
		2N / 2		2N / 2−1

на котором расположена точка х*. Величину l называют погрешностью метода дихотомии. Соответствующим выбором δ величину l можно сделать сколь угодно близкой к (b – a)/2N/2. Приняв приближённо

х* ≈(xN-1 + xN)/2,

получим, что погрешность вычисления х* не превышает величину l/2. Число f((xN-1 + xN)/2) будем считать минимальным значением f(x) на [a, b].

Сравнительный анализ указанных выше методов и обзор других методов одномерной минимизации можно найти в учебном пособии [1].

Методымногомернойбезусловнойоптимизации

Методы минимизации функций многих переменных можно разделить на две группы. Первую группу составляют регулярные методы оптимизации (или методы направленного поиска). Наиболее важными среди них являются так называемые методы спуска. Ко второй группе относятся методы случайного поиска.

В методах спуска направление движения к минимуму на каждом шаге выбирается из числа направлений убывания минимизируемой функции.

Говорят, что вектор h = (h1, h2, ..., hn) задает направление убывания функции f в точке x, если существует такое число α0 > 0, что

f(x + α		) < f(х)	(2.5)
	h

при всех 0 < α < α0. Сам вектор h также называют направлением убывания. Заменив неравенство, фигурирующее в (2.5), на противоположное,

получим определение направления возрастания.

Общая идея методов спуска состоит в следующем. Для определения точки x* локального минимума функции f(x) строится последовательность

Моделирование процессов и объектов в металлургии. Лаб. практикум

-30-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения

точек {x(k)} (k = 0, 1, 2, …), сходящаяся к точке х* таким образом, чтобы последовательность значений функции f(х(k)) была монотонно убывающей и ограниченной:

f(x(0)) ≥ f(x(1)) ≥ … ≥ f(x(k)) ≥ … ≥ f(x*).

Для различных методов спуска сначала выбирают начальную точку последовательности х(0). Дальнейшие приближения x(k) определяются соотношениями

x(k +1) = x(k ) + αk h(k) (k = 0, 1, 2, …),

(2.6)

где h(k) – вектор направления убывания; αk – положительная скалярная величина, называемая длиной шага.

Методы спуска различаются выбором направления убывания и длины шага. Наиболее известные из них − методы прямого поиска и градиентные методы.

Методы прямого поиска относятся к алгоритмам нулевого порядка, в которых используются только значения целевой функции. Мы рассмотрим подробно только один из них, а именно метод покоординатного спуска, или метод Гаусса-Зейделя. Практика показала, что этот метод эффективен и применим для широкого круга приложений.

Решение задачи (2.4) методом покоординатного спуска осуществляется по следующей общей схеме.

Выбирают произвольно начальную точку х(0) из области определения функции f(х). Приближения х(k) определяются соотношениями (2.6), где вектор направления убывания h(k) – это единичный вектор, коллинеарный ка- кому-либо из координатных направлений; величина αk является решением задачи одномерной минимизации

f(x(k) + t h(k)) → min, t R.

Решение этой задачи может быть найдено, в частности, каким-либо из методов одномерной минимизации.

Условием прекращения вычислительной процедуры при достижении заданной точности ε может служить неравенство

|| х(k + 1) − х(k) || < ε.

(2.7)

Моделирование процессов и объектов в металлургии. Лаб. практикум

-31-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения

Теоретически данный метод эффективен в случае единственного минимума функции. Его достоинством является простота алгоритма. Но на практике он оказывается слишком медленным. Поэтому были разработаны более сложные методы, использующие информацию не только о значениях функции, но и ее производных. Это так называемые градиентные методы спуска.

Далее везде будем считать, что f(x) и f(x) существуют и непрерывны, а компоненты градиента могут быть записаны в аналитическом виде или с достаточно высокой точностью найдены с помощью численных методов.

Все градиентные методы основаны на итерационной процедуре, реализуемой в соответствии с формулой (2.6), где вектор h(k) строится с помощью антиградиента функции f в точке x(k), т.е. вектора − f(x(k)), задающего направление наискорейшего убывания целевой функции f. Способ определения h(k) и αk на каждой итерации характеризует особенности применяемого метода. Например, поиск методом наискорейшего спуска (методом Коши)

сводится к построению последовательности приближений {xk} по формуле

(2.6), где

		(k )				f (x(k ) )
h			= −					,
						f (x(k ) )

|| f(x(k))|| – длина вектора градиента f(х(k)). Длина шага αk вычисляется путем решения задачи одномерной минимизации

ϕ(t) = f (x(k ) + t h (k ) ) → min, t Rn ,

с помощью какого-нибудь из методов одномерной минимизации. Условием окончания вычислительной процедуры является выполнение неравенства (2.7).

Метод наискорейшего спуска сходится быстрее, чем методы прямого поиска. Однако скорость его сходимости при решении ряда практических задач остается недопустимо низкой. Это вполне объяснимо, поскольку cкорость изменения переменных непосредственно зависит от длины вектора градиента || f(x(k))||, которая стремится к нулю, и отсутствует механизм ускорения движения к точке минимума на последних итерациях. Одно из главных преимуществ этого метода связано с его устойчивостью. Метод обладает важным свойством, которое заключается в том, что при достаточно малой длине шага αk на всех итерациях выполняется неравенство f (x(k+1)) ≤ f(x(k)). Благодаря этому свойству метод наискорейшего спуска, как правило, позволяет существенно уменьшить значение целевой функции при движении из

Моделирование процессов и объектов в металлургии. Лаб. практикум

-32-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Краткие теоретические сведения

точек, расположенных далеко от точки минимума, и поэтому часто используется при реализации градиентных методов в качестве начальной процедуры.

Методы случайного поиска отличаются от регулярных методов оптимизации намеренным введением элемента случайности. Они эффективны при решении сложных задач больших размерностей с произвольно заданными целевыми функциями, когда регулярные методы, как правило, неприменимы.

Различают ненаправленный случайный поиск, направленный случайный поиск без самообучения и с самообучением.

Ненаправленный случайный поиск (или метод статистических испыта-

ний, метод Монте-Карло) заключается в многократном моделировании независимых случайных вариантов решений из области допустимых, вычислении в каждом их них критерия оптимизации и запоминания наиближайшего к экстремуму. Метод Монтe-Карло относится к числу универсальных, поскольку позволяет решать многоэкстремальные задачи общего вида с отысканием глобальною экстремума. Основной недостаток метода – необходимость проведения большого числа испытаний для получения решения, достаточно близкого к оптимальному, т. е. наличие медленной сходимости к экстремуму.

Обзор других методов безусловной оптимизации можно найти в лите-

ратуре [1, 2, 3, 4, 5].

Порядоквыполненияработы

1.Изучить основные понятия теории оптимизации, классификацию и основные численные методы для решения задач оптимизации.

2.В соответствии с индивидуальным заданием исследовать заданную целевую функцию на экстремумы.

3.Учитывая проведенное исследование, выполнить вычислительный эксперимент в пакете прикладных программ MATHCAD.

4.Сравнить полученные результаты.

5.Оформить отчет, в который включить: титульный лист; формулировку цели лабораторной работы; теоретическое описание используемого численного метода и его сравнение с другими методами; геометрическую интерпретацию метода; индивидуальное задание на работу; анализ полученных результатов.

Моделирование процессов и объектов в металлургии. Лаб. практикум

-33-

ЛАБОРАТОРНАЯ РАБОТА 2. МЕТОДЫ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ

Порядок выполнения работы

Методикавыполненияработы впакетеMATHCAD

1.Получить задание.

2.Запустить пакет MATHCAD.

3.Ввести функцию в соответствии с вариантом задания.

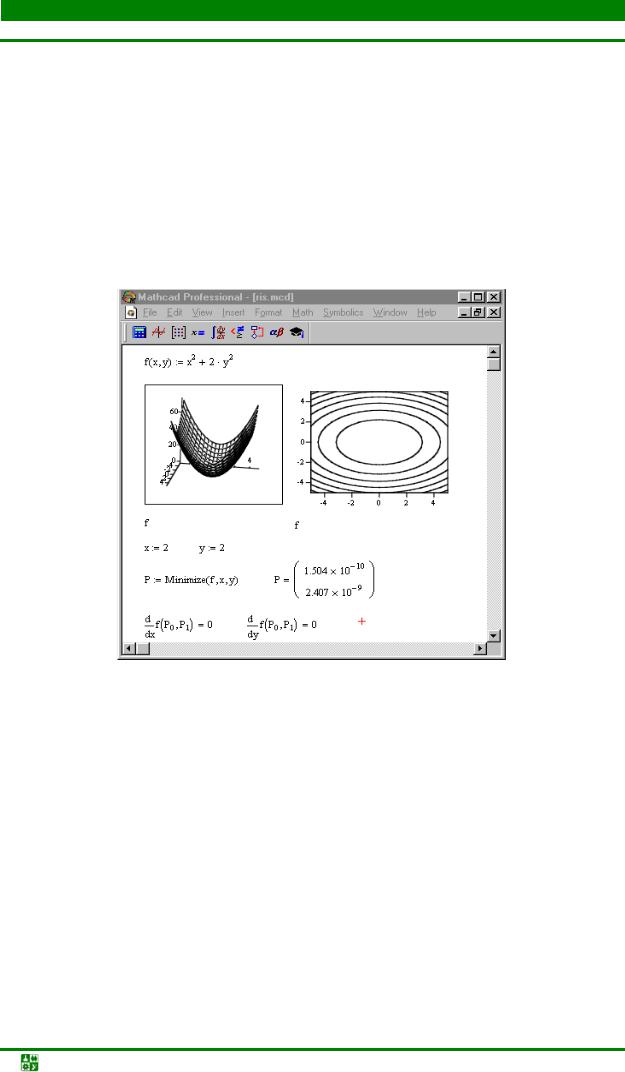
4.Построить график и линии уровня функции, используя компонент Graph. Изменяя диапазоны значений переменных x, y, найти область, в которой линии уровня функции представляют собой замкнутые кривые, концентрически вложенные друг в друга (рис. 2.1).

5.

Рис. 2.1. Пример решения задачи в пакете MathCad

6.Решить задачу безусловной оптимизации. Для этого задать начальные значения переменных в пределах найденной области и вычислить решение задачи с помощью встроенных функций Maximize или Minimize.

7.Проверить, удовлетворяет ли решение необходимым условиям оптимальности.

8.Распечатать результаты.

В пакете MATHCAD для решения задачи можно воспользоваться по-

мощью: Help → Solving and optimization → Maximizing or minimizing a function.

Моделирование процессов и объектов в металлургии. Лаб. практикум

-34-