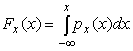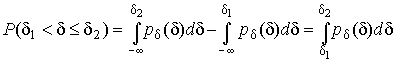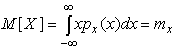- •Федеральное государственное автономное образовательное учреждение высшего и профессионального образования
- •1.2. Классификация и основные характеристики измерений
- •Глава 2. Физические величины и их единицы
- •2.1. Системы единиц физических величин
- •2.2. Относительные и логарифмические величины и единицы
- •Глава 3. Международная система единиц (си)
- •3.1. Установление единой международной системы единиц
- •3.2. Основные единицы си
- •3.3Дополнительные единицы си
- •3.4. Производные единицы си
- •3.5. Кратные и дольные единицы
- •Глава 4. Погрешности измерений. Случайные погрешности.
- •4.1. Основные понятия и определения
- •4.2. Описание случайных погрешностей с помощью функций распределения
- •4.3. Моменты случайных погрешностей
- •4.4. Виды распределения результатов наблюдения и случайных погрешностей
- •4.5. Точечные оценки истинного значения и среднеквадратического отклонения
- •4.6. Оценка с помощью интервалов
- •4.7. Проверка нормальности распределения результатов наблюдений
- •4.8. Обнаружение грубых погрешностей
- •Глава 5. Систематические погрешности.
- •5.1. Классификация систематических погрешностей
- •5.2. Способы обнаружения систематических погрешностей
- •5.3. Введение поправок. Неисключенная систематическая погрешность
- •Глава 6. Математическая обработка исправленных результатов измерений
- •6.1. Обработка результатов прямых равнорассеянных наблюдений
- •6.2. Обработка неравнорассеянных рядов наблюдений
- •6.3. Обработка результатов косвенных измерений
- •6.4. Критерии ничтожных погрешностей
- •Глава 7. Средства измерений. Погрешности средств измерений
- •7.1. Метрологические характеристики средств измерений
- •7.2. Нормирование метрологических характеристик средств измерений
- •7.3. Классы точности средств измерений
- •7.4. Регулировка и градуировка средств измерений
- •7.5. Калибровка средств измерений
- •7.6. Общие методы измерений
- •Часть 2. Организация метрологического контроля Глава 8. Метрологическое обеспечение (мо)
- •8.1. Государственная система обеспечения единства измерений
- •8.2. Цели, задачи и содержание мо
- •8.3. Система эталонов единиц фв
- •Глава 9. Метрологический надзор за средствами измерений
- •9.1. Государственные и отраслевые поверочные схемы
- •9.2. Виды поверок и способы их выполнения
- •9.3. Достоверность поверки
- •9.4. Определение объема поверочных работ
- •9.4. Определение объема поверочных работ
- •Глава 10. Средства измерений и контроля
- •10.1. Назначение измерений и контроля параметров технических устройств
- •10.2. Метрологическое обеспечение при разработке, производстве и эксплуатации технических устройств
- •10.3. Поверка, ревизия и экспертиза средств измерений
- •10.4. Государственные испытания средств измерений
- •Глава 11. Система эксплуатации и ремонта измерительной техники
- •11.1. Назначение и содержание работ по эксплуатации
- •11.2. Применение средств измерений и контроля
- •11.3. Техническое обслуживание средств измерений и контроля
- •Глава 12. Основы стандартизации
- •12.1. Государственная система стандартизации. Основные понятия и определения
- •12.2. Цели и задачи стандартизации
- •12.3. Виды и методы стандартизации
- •12.4. Категории и виды стандартов
- •12.5. Основные принципы стандартизации
- •12.6. Государственные и отраслевые системы стандартов
- •12.7. Международная стандартизация. Стандарты серий iso 9000 и iso 14000
- •Библиографический список
4.2. Описание случайных погрешностей с помощью функций распределения
Рассмотрим результат наблюдений Хза постоянной физической величинойQкак случайную величину, принимающую
различные значенияZ, в различных
наблюдениях за ней. Значения![]() будем
называть результатами отдельных
наблюдений.
будем
называть результатами отдельных
наблюдений.
Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения [1].
Под интегральной функцией распределения
результатов наблю-дений понимается
зависимость вероятности того, что
результат наблюдения
![]() вi-м опыте окажется меньшим некоторого
теку-щего значениях, от самой
величиных:
вi-м опыте окажется меньшим некоторого
теку-щего значениях, от самой
величиных:
|
|
(4) |
Здесь и в дальнейшем большие буквы используются для обозначения случайных величин, а маленькие - значений, принимаемых случайными величинами. Поскольку функция распределения вероятности представляет собой вероятность, то она удовлетворяет следующим свойствам:

На рис.2 показаны примеры функций распределения вероятности.
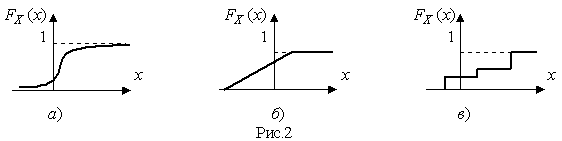
Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:
|
|
(5) |
Физический смысл f(x)состоит в том, что произведениеf(x)dxпредставляет вероятность попадания случайной величиныХв интервал отхдох + dx, т.е.
|
|
(6) |
Свойства плотности распределения вероятности:
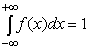 -
вероятность достоверного события равна
1;
иными словами, площадь, заключенная
между кривой дифференциальной функции
распределения и осью абсцисс, равна
единице;
-
вероятность достоверного события равна
1;
иными словами, площадь, заключенная
между кривой дифференциальной функции
распределения и осью абсцисс, равна
единице;
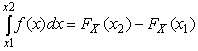 -
вероятность попадания случайной величины
в интервал от
-
вероятность попадания случайной величины
в интервал от![]() до
до![]() .
.
От дифференциальной функции распределения легко перейти к интегральной путем интегрирования:
|
|
(7) |
Размерность плотности распределения вероятностей, как это следует из формулы (7), обратна размерности измеряемой величины, поскольку сама вероятность - величина безразмерная.
Используя понятия функций распределения,
легко получить выражения для вероятностей
того, что результат наблюдений Хили случайная погрешность![]() примет
при проведении измерения некоторое
значение в интервале
примет
при проведении измерения некоторое
значение в интервале![]() или
или![]() .
.
В терминах интегральной функции
распределения имеем:
![]()
![]() т.е.
вероятность попадания результата
наблюдений или случайной погрешности
в заданный интервал равна разности
значений функции распределения на
границах этого интервала.
т.е.
вероятность попадания результата
наблюдений или случайной погрешности
в заданный интервал равна разности
значений функции распределения на
границах этого интервала.
Заменяя в полученных формулах интегральные функции распределения на соответствующие плотности распределения вероятностей согласно выражению (7), получим формулы для искомой вероятности в терминах дифференциальной функции распределения:
|
|
(8) |
|
|
(9) |
Таким образом, вероятность попадания результата наблюдения или случайной погрешности в заданный полуоткрытый интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границах этого интервала. Необходимо отметить, что результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины и по мере приближения к нему элементы вероятности их появления возрастают. Это дает основание принять за оценку истинного значения измеряемой величины координату центра тяжести фигуры, образованной осью абсцисс и кривой распределения, и называемую математическим ожиданием результатов наблюдений:
|
|
(10) |
В заключение можно дать более строгое определение постоянной систематической и случайной погрешностей.
Систематической постоянной погрешностьюназывается отклонение математического ожидания результатов наблюдений от истинного значения измеряемой величины:
|
|
(11) |
а случайной погрешностью- разность между результатом единичного наблюдения и математическим ожиданием результатов
|
|
(12) |
В этих обозначениях истинное значение измеряемой величины составляет
|
|
(13) |