
Реализация функций формулами
можно комбинировать булевы переменные с помощью булевых операций, получая булевы выражения, которые называются формулами.
Всякой формуле однозначно соответствует некоторая функция, при этом говорят, что формула реализует функцию.
ПРИМЕР:
Построить таблицу
истинности для формулы ![]() .
.
|
x1 |
x2 |
|
|
|
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Таким образом,
формула ![]() реализует
функцию
реализует
функцию![]() (тождественная
единица).
(тождественная
единица).
ПРИМЕР:
Построить таблицу
истинности для формулы ![]() .
.
|
x1 |
x2 |
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
Таким образом,
формула![]() реализует
функцию
реализует
функцию![]() (дизъюнкция).
(дизъюнкция).
Равносильные формулы
Формулы называются равносильными, если реализуют одну и ту же функцию.
Формула называется тождественно-истинной или тавтологией, если она реализует тождественную единицу.
Формула называется тождественно-ложной, если она реализует тождественный ноль.
Законы булевой алгебры
Законами булевой алгебры называются следующие равносильности:
1. Идемпотентность
![]() .
.
2. Коммутативность
![]() .
.
3. Ассоциативность
 .
.
4. Дистрибутивность
 .
.
5. Закон поглощения
![]() .
.
6. Закон склеивания
![]() .
.
7. Закон нуля
![]() .
.
8. Закон единицы
![]() .
.
9. Закон дополнения
![]() .
.
10. Инволютивность
![]() .
.
11. Законы де Моргана
![]() .
.
Тема 3.5. СДНФ и СКНФ
Определим степень следующим образом:
 ,
т.е.
,
т.е. ![]() ,
,![]() .
.
Выражение вида
![]()
называется полной совершенной элементарной конъюнкцией.
Можно дать другое определение: полной совершенной элементарной конъюнкцией называется конъюнкция переменных функции или их отрицаний, причем никакая из переменных не входит вместе с отрицанием этой переменной.
Выражение вида
![]()
называется полной совершенной элементарной дизъюнкцией.
Можно дать другое определение: полной совершенной элементарной дизъюнкцией называется дизъюнкция переменных функции или их отрицаний, причем никакая из переменных не входит вместе с отрицанием этой переменной.
Совершенной нормальной конъюнктивной формой (СКНФ) функции называется конъюнкция полных совершенных элементарных дизъюнкций.
Совершенной нормальной дизъюнктивной формой (СДНФ) функции называется дизъюнкция полных совершенных элементарных конъюнкций.
ПРИМЕР:
На этом примере покажем связь между таблицей истинности и функцией и ее совершенными нормальными формами:
|
х1 |
х2 |
|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
СДНФ:
![]()
![]()
СКНФ:
![]() .
.
При нахождении СДНФ пользуемся правилом: каждый набор аргументов определяет элементарную конъюнкцию, в которой значению 0 соответствует инверсия переменной, а значению 1 – сама переменная. СДНФ функции образуют те элементарные конъюнкции, которые соответствуют наборам аргументов, дающим 1.
|
х1 |
х2 |
|
элементарные конъюнкции |
|
0 |
0 |
1 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
0 |
|
|
1 |
1 |
1 |
|
При нахождении СКНФ пользуемся правилом: каждый набор аргументов определяет элементарную дизъюнкцию, в которой значению 1 соответствует инверсия переменной, а значению 0 – сама переменная. СКНФ функции образуют те элементарные конъюнкции, которые соответствуют наборам аргументов, дающим 0.
|
х1 |
х2 |
|
элементарные дизъюнкции |
|
0 |
0 |
1 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
0 |
|
|
1 |
1 |
1 |
|
Релейно-контактные схемы (РКС)
Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие - разомкнуты.
Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты,
подключенные к реле х, будем обозначать x1, ... xn, а размыкающие –
![]() Всей
схеме также можно поставить одно из
двух значений 1,
если
схема проводит ток,
и
0,
если
не проводит.
Это
значение есть функция переменных,
Всей
схеме также можно поставить одно из
двух значений 1,
если
схема проводит ток,
и
0,
если
не проводит.
Это
значение есть функция переменных,
![]() т.е.
логическая
функция.
Эту
функцию называют функцией проводимости
электрической цепи.
т.е.
логическая
функция.
Эту
функцию называют функцией проводимости
электрической цепи.
Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И, наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:

т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция - последовательным.
![]() называется
функцией проводимости данной
релейно-контактной схемы.
называется
функцией проводимости данной
релейно-контактной схемы.
Пример 1:
Построить функцию проводимости следующей схемы:
 (Рис.1)
(Рис.1)
Функция проводимости для такой схемы задается, очевидно, следующей таблицей:

По данной логической функции построим формулу - СКНФ:
![]()
Упростим это выражение
![]()
Построим более простую схему, имеющую ту же функцию проводимости, что и исходная:
![]()
(Рис.2)
Чтобы упростить релейно-контактную схему, не обязательно строить ее функцию проводимости. Можно написать соответствующую данной схеме формулу и упростить. Затем построить схему электрической цепи, моделирующую эту упрощенную формулу. Так, для электрической цепи, приведенной в данном примере
![]()
Пример 2:
Построить наиболее простую релейно-контактную схему по заданной функции проводимости f(x,y,z): f(0,1,0)=f(1,1,0)=f(1,1,1)=0.
Строим СКНФ:
![]()
т.к. эти сомножители обращаются в "0" на указанных наборах функции: (0,1,0), (1,1,0), (1,1,1).
Далее упрощаем формулу S:
![]()
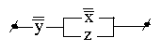 (Рис.3)
(Рис.3)
Пример 3:
Упростить схему:
 (Рис.4)
(Рис.4)
Решение:
составляем по схеме высказывание и упрощаем его:

Упрощенная схема имеет три переключателя вместо девяти
в исходной:
 (Рис.5)
(Рис.5)
Пример 4:
Имеется одна лампочка в лестничном пролете двухэтажного дома.
Постройте схему так, чтобы на каждом этаже своим выключателем можно было бы включать и выключать лампочку, независимо от положения другого выключателя.
Решение:
Функция
проводимости
 такой схемы должны обладать тем свойством,
что её значение меняется всякий раз,
когда меняется одного её аргумента.
Следовательно, например:
такой схемы должны обладать тем свойством,
что её значение меняется всякий раз,
когда меняется одного её аргумента.
Следовательно, например:

Используя
СДН-формулу, отсюда получаем:
 )
)

Пояснение: (x’=x1, y’=y1).
Пример 5:
Комитет состоит из пяти человек. Решение выносится большинством голосов. Если председатель «против», то решение не принимается.
Построить такую схему, чтобы, голосуя «за», каждый из пяти человек нажимал бы на кнопку, и в случае принятия решения, зажигалась бы сигнальная лампочка.
Решение: функция
проводимости
 будет принимать значение 1, только в
следующих случаях(x-председатель):
будет принимать значение 1, только в
следующих случаях(x-председатель):
|
x |
y |
z |
w |
e |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Составим СДНФ и упростим:



Список Литературы:
Новиков П.С.
Элементы математической логики. - М: Наука, 1973. 328с.
Стенюшкина В.А.
Математическая логика и теория алгоритмов: Учебное пособие.
Оренбург: ГОУ ОГУ, 2004. – 106 с.
