Векторная алгебра

Глава 2. ВЕКТОРНАЯ АЛГЕБРА

§1. Векторы, основные определения

Опр. Вектором называется направленный отрезок (отрезок, у которого различают начало и конец).

Если А – начало, В – конец, то вектор обозначают АВ (или AB ).

B

а

A AB

Часто вектор обозначают одной буквой а.

Опр. Длиной или модулем вектора АВ называется длина отрезка АВ. Обозначают АВ .

Опр. Вектор, у которого начало и конец совпадают, называется нуль-вектором и обозначают 0 . 0 0.

Будем рассматривать только свободные векторы, т.е. те, которые можно переносить в любое место пространства, сохраняя длину и направление.

Опр. Векторы a и b , расположенные на одной прямой или параллельных прямых, называются коллинеарными.

а	b	а
		b

Опр. Векторы а и b называются равными, если они:

1)имеют равные модули;

2)коллинеарны;

3)направлены в одну сторону.

Опр. Вектор а называется противоположным вектору а, если этот вектор имеет модуль, равный модулю вектора а, коллинеарен с ним, но направлен в противоположную сторону (вектор а – не нульа-вектор).

a

Опр. Векторы называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости.

1

§2. Линейные операции над векторами. Линейное пространство

I. Сложение векторов

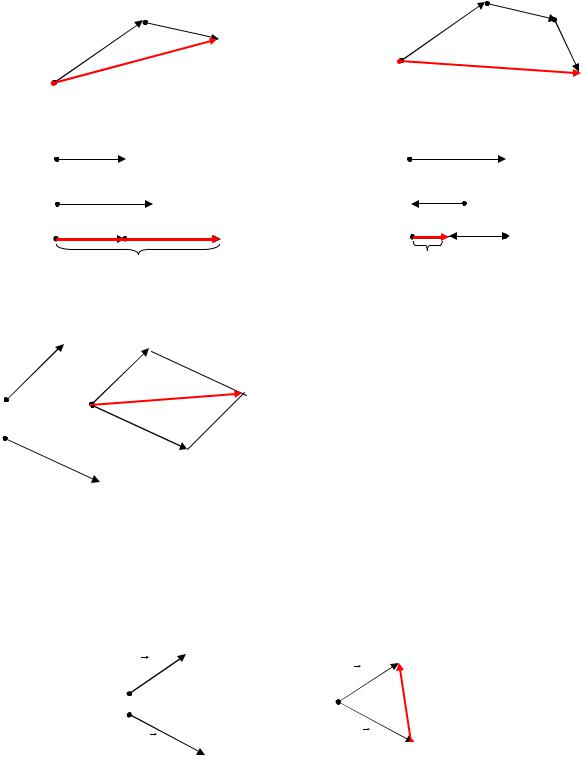
1) Правило треугольника

Суммой векторов a и b называется вектор c a b , который соединяет начало 1-го вектора с концом 2-го, при условии, что точка приложения 2-го

вектора находится в конце 1-го. Распространяется на любое конечное число
векторов.	b
b	a
a	d a b c	c
с a b

Частный случай. Сложение коллинеарных векторов.

a

a

b

b

a

a

b

b

с a b

b

с

a

2) Правило параллелограмма

a a

с a b

О

b b

Отложить от т. О вектор a и b . Построить на этих векторах как на сторонах параллелограмм. Вектор, служащий диагональю параллелограмма, проведенный из т. О, является суммой a b .

	II. Вычитание векторов	называется вектор c a b , который бу-
	Опр. Разностью двух векторов a и b
	дучи сложенным с вектором b дает вектор a .
	Если c a b, то c b a .
	Из определения вытекает правило построения a b .
	a
		a
				с a b
	b	b

c a b направлен из конца вычитаемого к концу уменьшаемого.

2

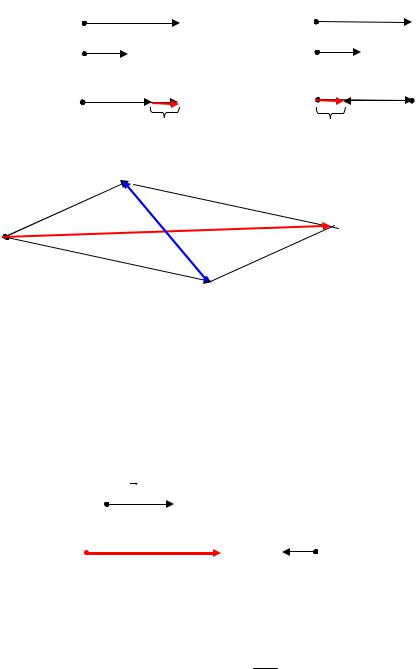
Частный случай.

a

a

b

или

b

a

a

b

- b

a

с a b

с a b

a b

Итак:

a b

b

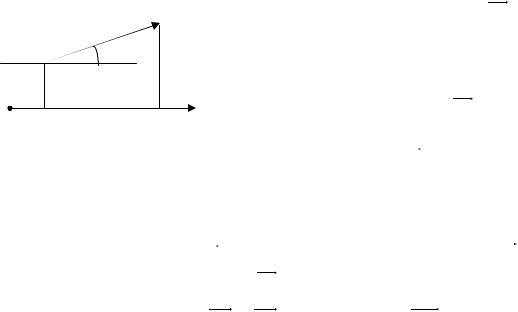
III. Умножение вектора на число

Опр. Произведением вектора a на число λ называется вектор λa :

1)коллинеарный вектору a ;

2)имеющий длину | a | | | | a |;

3)тоже направление, что и a , если 0 , противоположное направлению a , если 0.

a

		1 a
2a		2
a0 единичный вектор (орт) вектора	a ,	т.е. a0 коллинеарен a , одинако-

вого с ним направления,				| a0 | 1. Тогда
					a | a | a0		(3.1)
					или a0	1	a .
						| a |
Операции сложения векторов и умножения вектора на число называются
линейными.
Они обладают свойствами:
1) a b b	a,	a, b
2) (a b) c a (b c),					a, b, c
3) a 0 a,	a
4) a ( a) 0,		a
5) ( a) ( )a,			a,	, R
6) 1 a a,	a
					3

7)	( )a a a,	a, , R
8)	(a b) a b,	a, b, R

Множество векторов пространства, удовлетворяющих свойствам 1–8, образуют линейное (векторное) пространство, которое обозначается R3.

§3. Проекция вектора на ось

	B
A	φ
A1	B1
0 x1	x2

1.Проекция вектора на косинус угла

Пусть даны: l – некоторая ось и AB – произвольный вектор.

A1	проекция А на ось l, x1	координата A1 на l;
B1	проекция B на ось l, x2	координата B1 на l.
l Опр. Проекцией вектора		AB на ось называется

разность x2 x1

прl AB x2 x1 .

Свойства проекций

AB на ось l равна модулю вектора | AB |, умноженному между AB и осью l.

прl AB | AB | cos ,	где ( AB, l) .

2.Проекция суммы векторов на ось равна сумме проекций слагаемых векторов на ту же ось.

3.При умножении вектора на число проекция на ось также умножается на это число.

a прl ( a) прl a.

4.Проекции двух равных векторов на одну и ту же ось равны.

b прl a прl b .

§4. Линейная зависимость векторов. Базис

Рассмотрим n векторов a1, a2 ,...,an и n чисел 1, 2 ,..., n .

Опр. Выражение вида 1a1 2a2 ... n an называется линейной комбинацией векторов a1, a2 ,...,an .

4

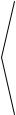
Опр. Векторы a1, a2 ,..., an

называются линейно зависимыми, если их линейная

комбинация равна нулю 1a1

2a2

... nan 0

при условии, что среди

1, 2 ,..., n

есть отличные от нуля.

Например,

1

0 , тогда 1a1

2a2

... n an ,

a

2 a

2

...

3

a

... n a

n

a

есть линейная комбинация a

2

,...,a

n

.

1

3

1

1

1

1

Итак, если векторы линейно зависимы, то хотя бы один из них можно представить в виде линейной комбинации остальных векторов.

Справедливо и обратно.

Опр. Векторы a1, a2 ,..., an называются линейно независимыми, если их линейная комбинация равна нулю 1a1 2a2 ... nan 0 при условии, что

1 2 ... n 0.

Итак,

		i	0	a1, a2 ,..., an			линейнозависимые
							a1 линейнаякомбинация
1a1	2a2	... n an 0					остальныхвекторов,
				a	, a	,..., a
		0					линейнонезависимые.
		i		1	2	n

1)Два коллинеарных вектора на плоскости линейно зависимы.

2)Два неколлинеарных вектора на плоскости линейно независимы.

Итак, для того, чтобы два вектора на плоскости были линейно независимы необходимо и достаточно, чтобы они были неколлинераны.

Теорема. Если на плоскости заданы два неколлинеарных вектора a и b , то любой третий вектор c плоскости может быть представлен в виде линейной

комбинации векторов a и b , т.е.

c 1a 2b .

(3.2)

Следствие 1. Всякие три вектора на плоскости линейно зависимы. Следствие 2. Если число данных векторов на плоскости больше трех, то они также линейно зависимы.

с 1a 2b с 1a 2b 0 d ... 0 e линейно зависимые.

Вывод. Максимальное число линейно независимых векторов на плоскости равно двум.

Аналогично Максимальное число линейно независимых векторов в пространстве равно трем.

Опр. Базисом на плоскости называется два любых линейно независимых вектора плоскости, т.е. пара неколлинеарных векторов .

5

Базисом в пространстве называется три любых линейно независимых вектора пространства, т.е. тройка некомпланарных векторов.

Рассмотрим разложение (3.2) на плоскости с 1a 2b , где a и b неколлинеарны. Коэффициенты 1 и 2 называются координатами вектора с в

базисе a, b .

Аналогично для разложения (3.3): d 1a 2b 3c ,		где		a, b, c не-
компланарные векторы пространства. Коэффициенты 1,		2 ,	3 называются
координатами вектора d в базисе a, b, c.				a3 (0;0;05)
Пример 4.1. Доказать, то векторы a1 (2;0;0),	a2 (0;1;0),
образуют базис в R3.

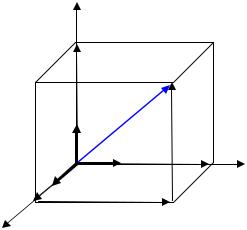
§5. Разложение вектора в декартовом базисе. Операции над векторами, заданными координатами. Длина вектора, направляющие косинусы

I. Прямоугольный декартов базис. Разложение вектора в декартовом базисе

	z						Рассмотрим пространство 0xyz, т.е.
		M3
							введем	в пространстве прямоугольную
				M			декартовую систему координат.
							Векторы i , j, k единичные векторы осей
	1	k	j				Оx, Oy,	Oz. Векторы	i , j, k	называются
							ортами.	Поскольку	i , j, k	некомпла-
					M2
	i	0	1			y	нарны, то они образуют базис в простран-
	1			P			стве, который называют декартовым ба-
x	M1						зисом.
Теорема. Любой вектор a ,					заданный в пространстве 0xyz, может быть пред-
ставлен в виде					a axi ay j az k .
										(3.4)

Такое представление вектора a называется разложением вектора в декартовом базисе или разложением вектора по ортам.

Проекции называются прямоугольными декартовыми координатами вектора a . Записывают a (ax ;ay ;az ) или a(ax ;ay ;az ) . Каждый вектор имеет

единственное представление в виде (3.4) в заданном базисе.

II. Операции над векторами, заданными их разложениями по ортам (за-

данными координатами)	и b bxi by j bz k .
Пусть даны два вектора a axi ay j az k

6

Тогда сумма векторов:

a b (ax bx )i (ay by ) j (az bz )k .

Разность векторов:

a b (ax bx )i (ay by ) j (az bz )k .

Произведение вектора на число

a axi ay j az k .

Итак, a b (ax bx )i (ay by ) j (az bz )k ,a axi ay j az k .

Пример 5.1. a 2i 3 j k ;

b i 2 j 4k . Найти 2a b.

III. Модуль вектора

По теореме о длине диагонали параллелепипеда

| OM |2 | OM 1 |2 | OM 2 |2 | OM 3 |2 или | a |2 ax 2 ay 2 az 2 .

| a | 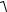ax2 ay2 az 2 модуль вектора a .

IV. Расстояние между двумя точками в пространстве

Рассмотрим вектор AB , где A(x1 , y1, z1 ), B(x2 , y2 , z2 ).

ax пр0 x AB x2

x1;

ay пр0 y AB y2 y1; az пр0 z AB z2 z1.

Тогда

(z2 z1 )k разложение AB по

ортам,

AB (x2 x1 )i

( y2 y1 ) j

где A(x1 , y1, z1 ), B(x2 , y2 , z2 ).

Расстояние между точками А и В равно |

AB | .значит

| AB |

(x

2

x )2

( y

2

y )2

(z

2

z )2

расстояние

между

точками

1

1

1

A(x1 , y1, z1 ), B(x2 , y2 , z2 ).

Частный случай.

Расстояние между точками на плоскости

| AB |

(x

2

x )2

( y

2

y )2

, где

A(x , y ),

B(x

2

, y

2

).

1

1

1

1

V. Направляющие косинусы

Направление вектора в пространстве определяется углами , , , кото-

рые вектор составляет с осями Ox, Oy, Oz. Косинусы этих углов, т.е. cos , cos , cos называются направляющими косинусами вектора.

По свойству 1 проекций:

7

a

x

пр

0 x

a

| a | cos

ax

ay

az

ay пр0 y a

| a | cos

cos

;

cos

;

cos

az

пр0 z a

| a | cos

| a |

| a |

| a |

или

ax

ay

az

cos

;

cos

;

cos

.

ax

2 ay

2 az

2

ax

2 ay

2

az

2

ax

2 ay

2

az

2

Тогда cos2 cos2 cos2 1.

VI. Условие коллинеарности двух векторов

Для того, чтобы два вектора a axi ay j az k

и

b bxi by j bz k

были коллинеарны, необходимо и достаточно, чтобы их проекции были пропорциональны

ax ay az условие коллинераности векторов. bx by bz

§6. Скалярное произведение векторов

I.Определение

Опр. Скалярным произведением векторов a и b называется число, равное произведению модулей этих векторов на косинус угла между ними.

a b | a | | b | cos(a b) .

Придадим (3.5) другой вид (по свойству 1 проекций).

| b | cos(a b) прab проекция b на ось, определяемую a .

| a | cos(a b) проекция a на ось, определяемую b . a b | a | прab | b | прb a.

II.Свойства скалярного произведения

1.Переместительное свойство a b b a. Доказательство из определения.

2. Сочетательное свойство относительно скалярного

( a) b a ( b) (a b) .

3. Распределительное свойство (a b) c a c b c.

(3.5)

(3.6)

множителя

8

			2
Пример 6.1. Векторы	a	и b образуют угол	3	. Зная, что | a | 10,	| b | 2
вычислить (a 2b)(3a	b).

4. Условие ортогональности векторов

По определению a b | a | | b | cos(a b) . a b 0 , если a 0 или b 0 , или

cos(a b) 0, т.е.	a b. Пусть	a и b – ненулевые векторы. Тогда
a b 0 a b .

Итак, для того, чтобы два ненулевых вектора были ортогональны, необходимо
и достаточно, чтобы их скалярное произведение равнялось нулю.
a b	a b 0.

Пример 6.2. При каком векторы a b и a b ортогональны, если
| b | 5? Ответ: 3.
5
III. Скалярное произведение векторов, заданных координатами
Даны два вектора a axi	ay j az k и	b bxi by j bz k . Найти a
Найдем предварительно скалярное произведение ортов.
i i | i | | i | cos 0 1;	j j 1;	k k 1;

| a | 3,

b.

i j | i | | j | cos 0;	i k 0;	j k 0.
2
Тогда
a b (axi ay j az k )(bxi by j bz k ) axbxi i aybx j i azbx k i axby i j
azby k j axbz i k aybz j k azbz k k axbx ayby azbz .
a b axbx ayby azbz скалярное произведение векторов, заданных коор-
динатами.
Если a b, то axbx ayby	azbz 0 условие перпендикулярности векторов.

IV. Угол между векторами в пространстве

По определению a b | a | | b | cos(a b) , значит cos(a b) | aa| |bb | .

Пример 6.3. Даны вершины четырехугольника А(1, -2, 2), В(1, 4, 0), С(-4, 1, 1), D(-5, -5, 3). Вычислить угол между его диагоналями. Ответ: 90о.

9

§7. Векторное произведение векторов

I. Определение

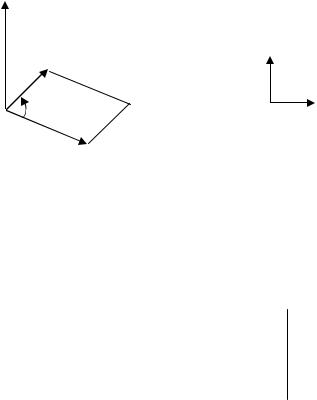
Опр. Векторным произведением вектора a на вектор b называется вектор с , который определяется следующим образом:

1) модуль вектора с численно равен площади параллелограмма, построенного

на векторах a и b как на сторонах

| с | | a | | b | sin(a b);

2)вектор c перпендикулярен перемножаемым векторам, т. е. c a , c b;

3)направление вектора с таково, что если смотреть с его конца (вдоль векто-

ра), то поворот по кратчайшему пути от вектора a к вектору b виден совершающимся против часовой стрелки.

,b,c ориентированы как i , j, k прав. тройка).

Обозначается: Част- c

b

a

c a b или [a,b].

ные случаи: i

i

j k , j k i , k i j

k

j

II.Свойства векторного произведения

1. При перестановке сомножителей векторное произведение меняет знак a b b a .

Доказательство. c1 a b ; c2		b a
1)	| c1 | | c2 | т.к. равныSпараллелограмма		a b b a
2)	c1 ,c2 a иb	с1 с2 или
3)	c1 || c2 , нопротивоположнонаправлены

2. ( a) b a ( b) (a b) сочетательное свойство относительно скалярного множителя, т.е. числовой множитель можно выносить за знак век-

произведения.

3.(a b) c a c b c распределительное свойство.

4.Условие коллинеарности векторов.торного

10