Решение систем линейных уравнений методом гаусса

Рассмотрим систему mлинейных уравнений сnнеизвестными:

(1)

Метод Гаусса основан на последовательном исключении неизвестных с помощью элементарных преобразований системы уравнений.

С помощью элементарных преобразований исходная линейная система уравнений (1) может быть преобразована в линейную систему уравнений ступенчатого вида, эквивалентнуюданной, и все решения могут быть найдены последовательно, начиная с последнего уравнения.

В алгоритме Гаусса все преобразования производятся непосредственно над уравнениями системы. Однако этот алгоритм можно существенно упростить, если соответствующие элементарные преобразования осуществлять над строками расширенной матрицы системы.

Матрицей системыуравнений (1) называется матрица, составленная из коэффициентов при неизвестных

.

Расширенной матрицейсистемы уравнений (1) называется матрица, получаемая из матрицы системы путем добавления столбца свободных членов:

.

Очевидно, что каждому элементарному преобразованию системы уравнений (1) соответствует аналогичное элементарное преобразование над строками матрицы . Следовательно, в алгоритме Гаусса можно от элементарных преобразований над системой (1) перейти к соответствующим элементарным преобразованиям над строками расширенной матрицы системы.

Задание 1

Решить систему уравнений методом Гаусса:

Решение

С помощью элементарных преобразований преобразуем данную систему уравнений к ступенчатому виду. Исключим х₁ из второго и третьего уравнений системы. Для этого умножим первое уравнение системы на 4 и вычтем из второго, а затем умножим на 5 и вычтем из третьего. Получим систему линейных уравнений, эквивалентную данной, в виде

Далее разделим второе уравнение системы на (-5), а третье умножим на (-1). Система примет вид

Исключим теперь х₂из последнего уравнения, умножив второе уравнение системы на (-11) и сложив его с третьем:

Из последнего уравнения определяем х₃= 3. Поставив найденное значениех₃во второе уравнение, получимх₂= 2. Знаях₂и х₃, можно из первого уравнения системы определитьх₁= 1.

Очевидно, что операции над уравнениями системы аналогичны операциям над строками ее расширенной матрицы.

В данной системе число уравнений m= 3 и число неизвестныхn= 3.

Составим матрицу системы и ее расширенную матрицу:

и .

Определим ранги этих матриц. В расширенной матрице пунктирной чертой отделим столбец свободных членов, чтобы отдельно можно было видеть и преобразование матрицы. Посредством последовательных элементарных преобразований над строками расширенной матрицы системы получим следующую систему эквивалентных матриц:

. (2)

Полученная в результате элементарных преобразований ступенчатая матрица имеет три ненулевые строки, а значит, ее ранг равен r=3. Следовательно, и ранг расширенной матрицыr(A′)= 3. Очевидно, что матрица системы также имеет три ненулевые строки, а значит, и ее ранг также равенr(А)=3.

Так как r(A)=r(A′) = n = 3, то в соответствии с теоремой Кронекера - Капелли система совместна и имеет единственное решение.

Полученной в результате элементарных преобразований ступенчатой матрице (2) соответствует система уравнений

которая уже была получена в результате элементарных преобразований исходной системы уравнений.

Из последнего уравнения определяем х₃= 3. Поставив найденное значениех₃во второе уравнение, получимх₂= 2. Знаях₂и х₃, можно из первого уравнения системы определитьх₁= 1.

Ответ:х₁= 1;х₂= 2;х₃= 3.

Задание 2

Исследовать систему уравнений:

Решение

В данной системе число уравнений m= 3, а число неизвестныхn= 2.

Составим матрицу системы и ее расширенную матрицу

и .

Определим ранги этих матриц. В расширенной матрице , как и прежде, пунктирной чертой отделим столбец свободных членов, чтобы отдельно можно было видеть и преобразование матрицы. Посредством последовательных элементарных преобразований над строками расширенной матрицы системы получим следующую систему эквивалентных матриц:

. (4)

Полученная в результате элементарных преобразований ступенчатая матрица имеет две ненулевые строки, а значит, ее ранг равен r=2. Следовательно, и ранг расширенной матрицыr(A′)= 2. Очевидно, что матрица системы также имеет две ненулевые строки, а значит, и ее ранг также равенr(А)=2.

Так как r(A)=r(A′) = n = 2, то в соответствии с теоремой Кронекера - Капелли система совместна и имеет единственное решение.

Полученной в результате элементарных преобразований ступенчатой матрице (4) соответствует система уравнений

Из последнего уравнения системы получаем х₂ = 1, а затем из первого находим х₁ = 2.

Ответ:х₁= 2;х₂= 1.

Задание 3

Исследовать систему уравнений:

Решение

В данной системе число уравнений m= 3, а число неизвестныхn= 3.

Составим расширенную матрицу системы:

.

Определим ранг этой матрицы. В расширенной матрице , как и в предыдущих примерах, пунктирной чертой отделим столбец свободных членов, чтобы видеть и преобразование матрицы системы. Посредством последовательных элементарных преобразований над строками расширенной матрицы системы получим следующую систему эквивалентных матриц:

. (5)

Полученная в результате элементарных преобразований ступенчатая матрица имеет три ненулевые строки, а значит, ее ранг равен r=3. Следовательно, и ранг расширенной матрицы и ранг матрицы системыr(A′)=r(А) = 3. А так какr(A)=r(A′) = n = 3, то в соответствии с теоремой Кронекера - Капелли система совместна и имеет единственное решение.

Полученной в результате элементарных преобразований ступенчатой матрице (5) соответствует система уравнений

Из последнего уравнения системы получаем х₃ = -2, а затем из второго и первого уравнений находим х₂ = -2 и х₁ = 3.

Ответ:х₁= 3;х₂= -2;х₃= -2.

Задание 4

Решить систему уравнений методом Гаусса:

Решение

Преобразуем данную систему уравнений путем элементарных преобразований к ступенчатому виду:

Так как два последних уравнения системы противоречивы, то система не совместна.

Такой же результат получим, оперируя строками расширенной матрицы системы.

В данной системе число уравнений m= 4 и число неизвестныхn= 4.

Составим расширенную матрицу системы:

.

Определим ранг этой матрицы:

Ранг полученной в результате элементарных преобразований матрицы равен r=4, так как она имеет четыре ненулевые строки. Поэтому и ранг расширенной матрицыr(A′)= 4. Однако ранг матрицы системы r(А) =3. То естьr(А)< r(A′), а, следовательно, в соответствии с теоремой Кронекера – Капелли система несовместна, т.е. не имеет решений.

Ответ:система несовместна.

Задание 5

Решить систему уравнений методом Гаусса:

(7)

Решение

Преобразуем данную систему уравнений путем элементарных преобразований к ступенчатому виду:

Из последнего уравнения системы находим . Тогда из второго уравнения можно определить , а из первого .

Эта система имеет бесконечное множество решений. Переменные и -свободные переменные- могут принимать любые значения, а переменные , и , которые называютсябазисными переменными, однозначно определяются заданием неизвестных и .

Общим решениемсистемы линейных уравнений называется выражение базисных переменных через свободные

Частным решениемсистемы линейных уравнений называется решение, полученное из общего для некоторой совокупности произвольных значений свободных переменных. Например, для системы уравнений (7) прииполучим частное решение

Очевидно, что данная система уравнений имеет бесчисленное множество частных решений.

Базисным решениемсистемы линейных уравнений называется решение, полученное из общего при условии равенства нулю свободных переменных. Например, для системы уравнений (2) прииполучим базисное решение

К такому же результату можно прийти, оперируя строками расширенной матрицы системы.

В данной системе число уравнений m= 3, а число неизвестныхn= 5.

Составим расширенную матрицу системы:

.

Определим ранг этой матрицы:

. (8)

Ранг полученной в результате элементарных преобразований ступенчатой матрицы равен r=3. Поэтому и ранг расширенной матрицы, и ранг матрицы системыr(A′)=r(А) = 3. Следовательно, система совместна, но так какr(A′)=r(А) = 2 <n=5 то в соответствии с теоремой Кронекера – Капелли система неопределенна, т.е. имеет бесконечное множество решений.

Полученной в результате элементарных преобразований ступенчатой матрице (8) соответствует система уравнений

, (9)

которая была получена ранее, при элементарных преобразованиях исходной системы уравнений.

За базисные переменные можно принять любые три, определитель из коэффициентов при которых отличен от нуля, например, х₁, х₃ и х₅, так как .Тогда свободными переменными будут х₂ и х₄ . Преобразуем систему уравнений (9) к виду

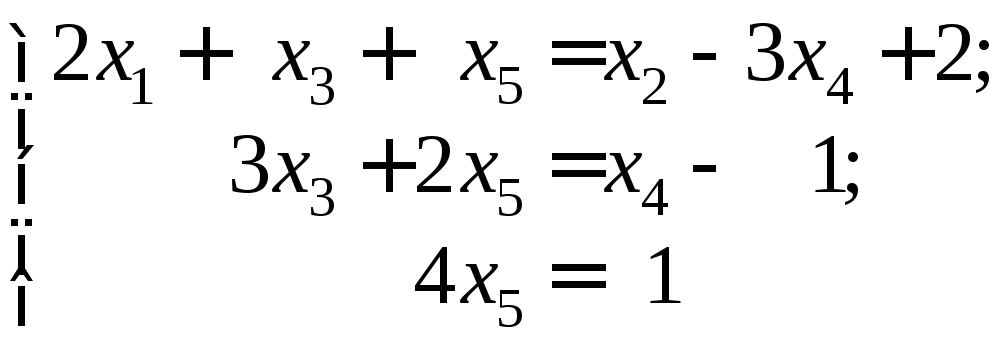
и выразимх₁, х₃ и х₅ через х₂ и х₄. Из последнего уравнения системы получаем , затем из второго находими, наконец, из первого.

Следовательно, общим решениемисходной системы уравнений является

Полагая, например, и, получим одно из частных решенийданной системы линейных уравнений

При иполучимбазисное решениеданной системы линейных уравнений

Задание 6

Решить систему уравнений методом Гаусса:

Решение

Преобразуем данную систему уравнений путем элементарных преобразований к ступенчатому виду:

Очевидно, что данная система четырех линейных уравнений сводится к системе двух уравнений вида

(10)

В качестве свободных переменных можно взять, например, переменные и , а переменные и - принять за базисные. Тогда система уравнений (10) преобразуется к виду

Из последнего уравнения системы находим , а из первого уравнения можно определить .

Эта система имеет бесконечное множество решений.

Общим решениемисходной системы уравнений является

Полагая, например, иполучим одно из частных решенийданной системы линейных уравнений

При иполучимбазисное решениеданной системы линейных уравнений:

Тот же результат получается, если оперировать строками расширенной матрицы системы.

В данной системе число уравнений m= 4, а число неизвестныхn= 4.

Составим расширенную матрицу системы:

.

Определим ранг этой матрицы:

(11)

Ранг полученной в результате элементарных преобразований ступенчатой матрицы равен r=2. Поэтому и ранг расширенной матрицы, и ранг матрицы системыr(A′)=r(А) = 2. Следовательно, система совместна, но так какr(A′)=r(А) = 2 <n=4 то в соответствии с теоремой Кронекера – Капелли система неопределенна, т.е. имеет бесконечное множество решений.

Полученной в результате элементарных преобразований ступенчатой матрице (11) соответствует система уравнений

(12)

которая была получена ранее, при элементарных преобразованиях исходной системы уравнений.

За базисные переменные можно принять любые две, определитель из коэффициентов при которых отличен от нуля, например, х₁ и х₂, так как . Тогда свободными переменными будут х₃ и х₄ . Систему уравнений (12) преобразуем к виду выразимх₁ и х₂ через х₃ и х₄ и найдем общее решение исходной системы уравнений

Полагая, например, иполучим одно из частных решенийданной системы линейных уравнений

При иполучимбазисное решениеданной системы линейных уравнений.

12