Последнее выражение перепишем в виде

(25)

Лекция 13

Тема 3.1 Термонапряжения при индукционном нагреве. Постановка задачи. Алгоритм решения мкэ

Среди различных численных методов решения механических задач (МКГ, МКР) в данном случае выбор делается в пользу метода конечных элементов, поскольку он выгодно отличается от остальных.

Расчет электродинамических усилий, перемещений и концентрации напряжений в элементах конструкций сводится к определению компонентов векторов перемещений точек тела

, (1)

деформаций

(2)

и напряжений

, (3)

где символ «Т» означает операцию транспонирования матриц. Все эти неизвестные являются функциями координат точек тела.

Отметим, что представление напряжений и деформаций (как и некоторой совокупности скалярных величин) в виде многомерных векторов, составленных из компонентов тензоров – удобный прием вычислительной математики, позволяющий использовать аппарат матричной алгебры. По существу, конечно, оно не имеет физического обоснования и справедливо только при неизменной системе координат, поскольку компоненты напряжений и деформаций образуют тензоры.

В статической задаче компоненты вектора напряжений должны удовлетворять уравнениям равновесия

(4)

где ,,– компоненты вектора массовых сил. Три других уравнения равновесия в виде сумм моментов внутренних сил относительно координатных осей приводят к известным условиям парности касательных напряжений.

Для точек, лежащих на поверхности тела, компоненты напряжений должны обеспечивать выполнение краевых условий

, (5)

где ,,– компоненты вектора внешних поверхностных нагрузок;l, m, n - направляющие косинусы единичной нормали к поверхности тела.

Компоненты вектора перемещений однозначно связаны с компонентами вектора деформаций соотношениями Коши:

, ,,,,. (6)

Эти уравнения, справедливые для малых деформаций, выражают условия сплошности тела. На той части поверхности тела, где заданы перемещения, функции удовлетворяют кинематическим граничным условиям вида

(7)

где – известные функции координат. Заметим, что поверхности и должны образовывать полную поверхность(S) тела, то есть .

Замкнутая система уравнений краевой задачи получается из уравнений (4)-(7), дополненных физическими уравнениями, связывающими векторы напряжений и деформаций. Последние строятся на основе физических и математических моделей конструкционных материалов.

Интегральную формулировку задачи можно получить, например, на основе принципа возможных перемещений, согласно которому в состоянии равновесия работа всех внешних и внутренних сил на соответствующих им возможных перемещениях равна нулю:

, (8)

где первое слагаемое представляет собой вариацию потенциальной энергии деформации, второе – работувнешних поверхностных и объемных сил, то есть

. (9)

Выполнение принципа возможных перемещений равносильно выполнению дифференциальных уравнений равновесия (4), а также краевых условий (5) и (7). Уравнения сплошности в форме (6) предполагаются выполненными. Остается дополнить уравнение (8) физическими уравнениями.

Непосредственно из принципа возможных перемещений можно получить вариационный принцип Лагранжа в виде

, (10)

где Э – полная потенциальная энергия тела, определяемая как разность между работой внутренних и внешнихсил.

В осесимметричной задаче данной теории рассматривается тело вращения (рис. 1), внешние нагрузки на котором (а также температура) симметричны относительно его оси.

Рис. .1 Тело вращения с внешними нагрузками, симметричными относительно его оси

При этом перемещения, деформации и напряжения также симметричны относительно оси и являются функциями двух координат. Векторы деформаций и напряжений в осесимметричной задаче имеют вид

, (11)

, (12)

где верхний индекс «Т» означает операцию транспонирования.

Соотношения Коши записываются в форме

, (13)

где u, w – компоненты перемещений, r – текущий радиус.

Для изотропного материала уравнения упругости принимаются в виде

, (14)

где матрица упругости

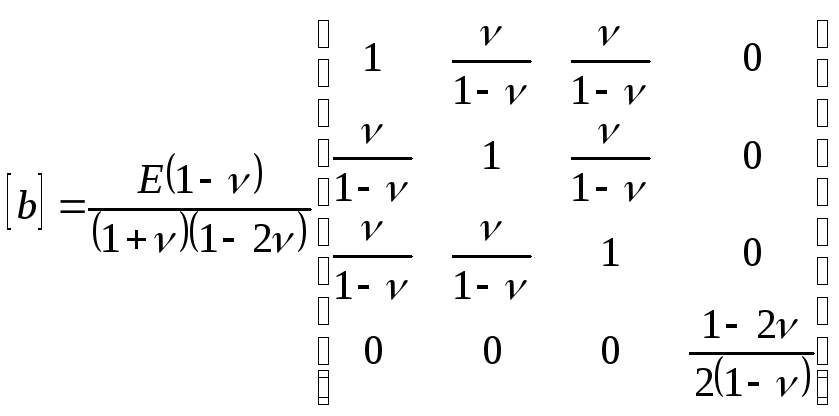; (15)

вектор дополнительных деформаций

. (16)

Если эти деформации температурные, то

. (17)

В соотношениях (15)-(17): Е, - упругие постоянные материала;- коэффициент линейного температурного расширения;- перепад температур.

Для некоторого осесимметричного конечного элемента с вершинами i, j, m (рисунок) вектор искомых узловых перемещений имеет следующую структуру

, (18)

а перемещения точек внутри элемента представляются в виде:

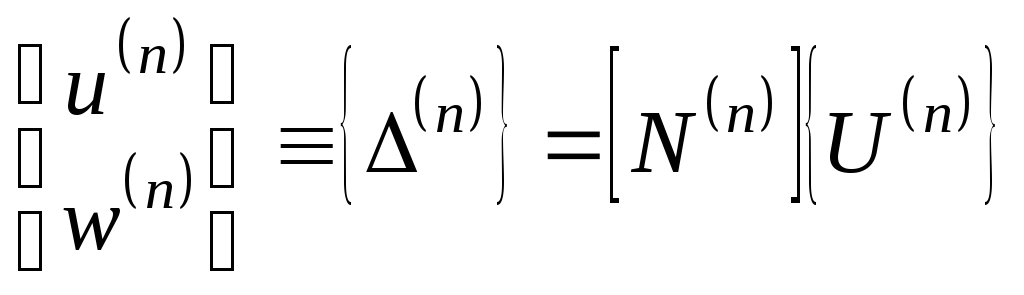, (19)

где матрица функций формы элементов:

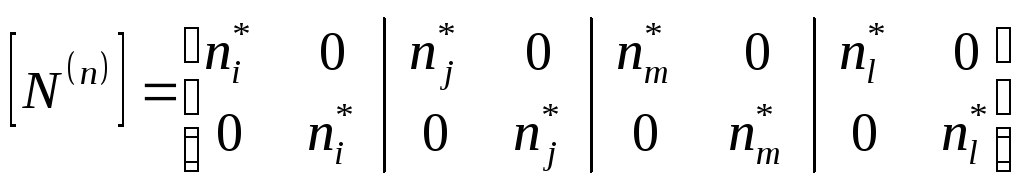
и т.д., (20)

где – площадь элемента, а коэффициенты,,и другие ()определяются с помощью зависимостей типа

. (21)

Вектор деформаций выражается через вектор узловых перемещений с помощью зависимости

, (22)

в которой матрица градиентов , как и в плоской задаче, состоит из трех блоков

, (23)

каждый из которых имеет структуру типа

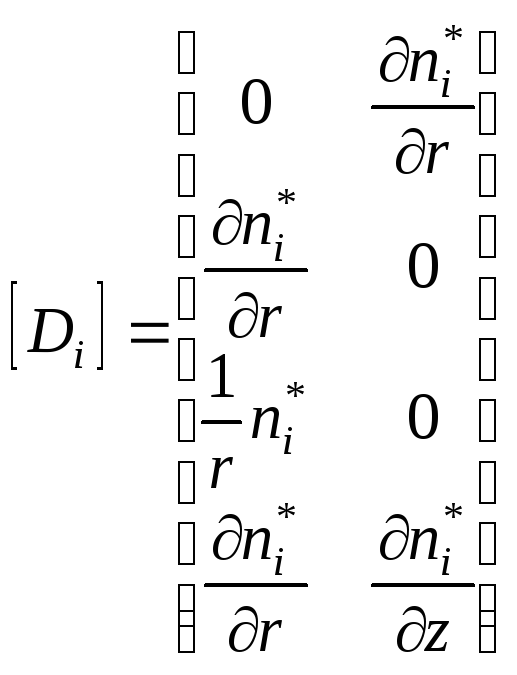, . (24)

Однако, в отличие от плоской задачи, здесь зависит от координатыr, следовательно, деформации внутри конечного элемента в общем случае не будут постоянными.

Теперь с помощью соотношения (23) выразим напряжения (14) в конечном элементе через узловые перемещения.

Получим

. (25)

Система разрешающих уравнений МКЭ для осесимметричной задачи имеет тот же вид, что и для объемной, то есть

, (26)

где матрица жесткости в конструкции в целом описывается как

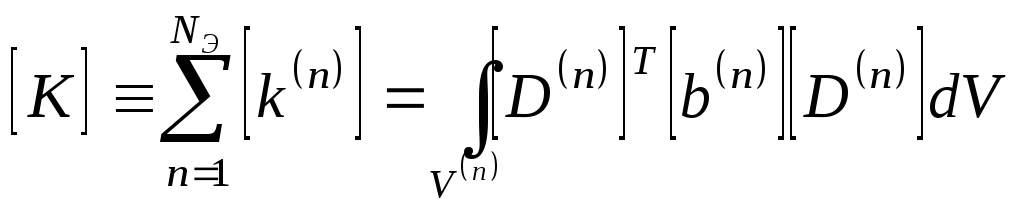; (27)

- число элементов; - объем элемента.

Вектор узловых сил, как и в плоской задаче, получается суммированием по всем элементам:

, (28)

то есть векторов узловых сил, эквивалентных внешним объемным и поверхностнымнагрузкам, а также дополнительным деформациям.

Эти векторы, отнесенные к конечным элементам (n = 1, 2,…, N_Э), находятся из следующих соотношений:

, (29)

, (30)

, (31)

где матрицы распределенных объемных и поверхностных нагрузок имеют соответственно следующую структуру:

; . (32)

В осесимметричной задаче, как и в плоской, матрица жесткости конечного элемента имеет вид

. (33)

Однако матрица градиентов в данном случае зависит от координат, что осложняет интегрирование уравнения (33). В практических расчетах рассматриваемый интеграл можно вычислить приближенно, определив матрицыидля центра тяжести конечного элемента с координатами

, . (34)

С учетом этого, а также соотношения , из (30) найдем

. (35)

Аналогичным образом могут быть найдены и приближенные значения векторов узловых сил (26)-(28). Опыт показывает, что при достаточно мелкой сетке конечных элементов рассмотренный прием обеспечивает приемлемую точность вычислений. Отметим, что точный расчет интегралов (26)-(30) уравнений может быть выполнен с помощью L-координат.