Лекция 6.

Тема 1.5 Нагрев неограниченной пластины. Решение методом преобразования Фурье

Дана неограниченная пластина толщиной 2Rпри температуре. Теплообмен с окружающей средой происходит при ГУ2. Нагрев осуществляется переменным источником

(60)

НУ T(x,0)=f(x) (61)

(62)

ГУ2 принимаем в виде

(63)

Решение найдём методом интегрального преобразования Фурье

Воспользуемся косинус - преобразованием Фурье

(64)

И формулой перехода от изображения функции к её оригиналу

(65)

Умножая обе части дифференциального уравнения (60) на и интегрируя в пределах от 0 доRс учётом ГУ(72) и(73) получим

(66)

Где (67)

Решение этого уравнения б

(68)

Для определения C(n) воспользуемся Н.У. (71)

(69)

Тогда

(70)

Для удобства перехода к оригиналу по соотношению (65) применяем решение для изображение (68) в виде

(71)

Причём во втором слагаемом n=1,2,3….

Имеем:

(72)

Где (73)

Переход от изображения к оригиналу производим по формуле (65)

(74)

Решение (74) является общим решением поставленной задачи

Решение в обобщённых переменных

(75)

Здесь ;;

Из (75) можно получить ряд интересных для практически частных решений

1.

(76)

Где 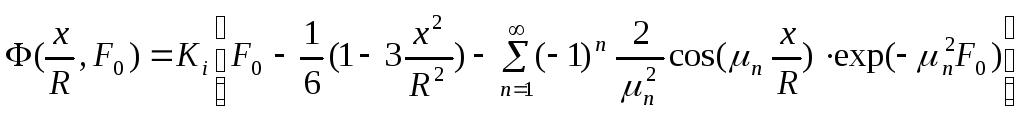(77) является решением задачи при отсутствии источников тепла

2. источник тепла – линейная функция от координаты

(78)

3. Источник тепла – линейная функция времени

(79)

Где - критерий Предводителева, равный максимальной скорости изменения относительной удельной мощности источника тепла по числу Фурье

(80)

k- постоянная, численно равная максимальной относительной скорости изменения удельной мощности источника тепла,- удельная мощность источника тепла при

Лекция 7

Тема 1.6 Нагрев неограниченного цилиндра

Решение задачи нагрева цилиндра произведем с помощью преобразования Ханкеля

(81)

Краевые условия

T(r,0)=f(r); (82)

(83)

(84)

Для решения задачи воспользуемся конечным интегральным преобразованием Ханкеля

(85)

Где p– корень характеристического уравнения

(86)

Переход от изображения к оригиналу осуществляется по формуле

(87)

Применяя преобразование (85) к дифференциальному уравнению (81) с учётом ГУ (83), (84) получим

(88)

Где (89)

Решение обыкновенного диф. уравнения имеет вид

(90)

Для определения постоянной C(p) воспользуемся начальным условием (81). Из решения (89) следует, что при

(91)

Кроме того, по определению изображения имеем

(92)

Следовательно

(93)

Если вместо C(p) подставим выражение (93) в решение (90), то получим решение задачи для изображения

Для перехода к оригиналу из решения (89)

(95)

Где (96)

Подставив значение ив формулу (97) получим решение

(97)

Обозначим

(98)

Где (99)

- корни характеристического уравнения

Если начальное распространение темперfтуры равномерное , апринята равной 0, то прирешение (98) можно записать так

(100)

Где (101)

Частные случаи

1. Постоянный источник тепла

(102)

2. Источник тепла – параболическая функция

(103)

(104)

Где - критерий Предводителева