stat021012

И найдем произведение сумм квадратов отклонений.

6. Определяем коэффициент r линейной парной корреляции, используя приведенную формулу.

41

7. Оцениваем тип и глубину корреляционной связи между признаками Х и У.

8. Вычисляем среднюю ошибку коэффициента корреляции. Обратите внимание, что вид формулы в строке формул соответствует приведенной выше.

42

9. Определяем критерий достоверности коэффициента корреляции.

10. Из таблицы 1 для числа степеней свободы ν = n - 2 определяем стандартные значения критериев Стьюдента, соответствующие трем порогам достоверности: 0,95; 0,99; 0,999.

43

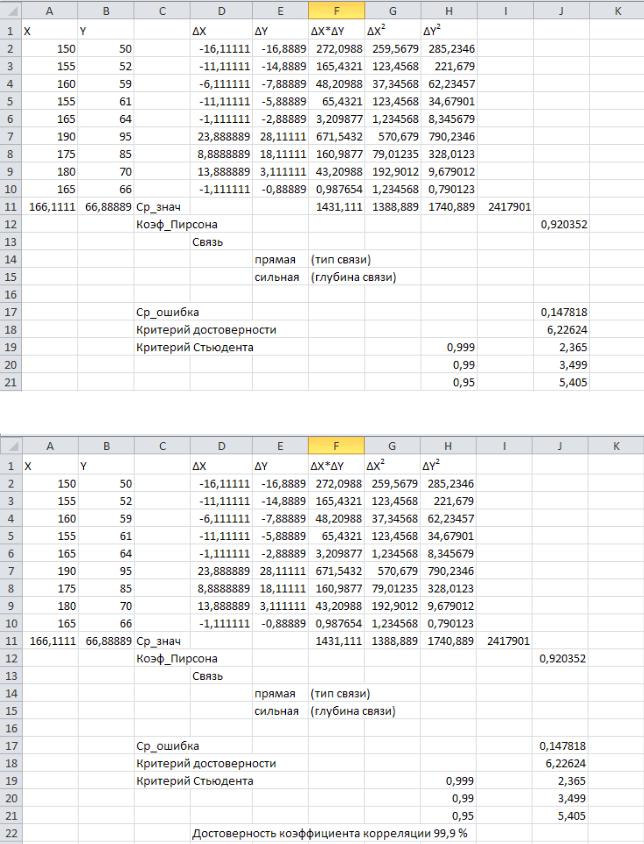
11. Сравниваем критерий достоверности tr со стандартными значениями критериев Стьюдента и делаем вывод о достоверности коэффициента корреляции.

44

13. Вычислим коэффициент корреляции Пирсона с помощью функции КОРРЕЛ. В качестве массивов 1 и 2 выберем наши массивы X и Y.

45

14. Построим корреляционное поле, используя вкладку Диаграммы, и выбрав тип диаграммы Точечная.

Т.к. диаграмма смещена в правый верхний угол, поместим ее в центр координатной плоскости. Для этого изменим минимальные значения осей X и Y.

46

15.Не забудьте дать Листу 3 название Задание 3

47

Универсальных рецептов установления корреляции между немонотонно и нелинейно связанными переменными на сегодняшний день не существует. Отметим, что большое (близкое к +1 или к -1) значение коэффициента корреляции говорит о связи переменных, но ничего не говорит о причинно-следственных отношениях между ними. Так, например, из высокой корреляции температуры воздуха за окном и времени суток нельзя делать вывод о том, что движение солнца обусловлено изменениями температуры воздуха.

Итак, корреляционный анализ позволяет устанавливать наличие или отсутствие зависимости между переменными. Другим инструментом, дающим ответ на этот вопрос, является дисперсионный анализ, который не является предметом рассмотрения данной работы.

Регрессионный анализ

Если корреляционный и дисперсионный анализ дают ответ на вопрос, существует ли взаимосвязь между переменными, то регрессионный анализ предназначен для того, чтобы найти «явный вид» этой зависимости.

Цель регрессионного анализа – найти функциональную зависимость между переменными. Для этого предполагается, что зависимая переменная (иногда называемая откликом) определяется известной функцией (иногда говорят – моделью), зависящей от зависимой переменной или переменных (иногда называемых факторами) и некоторого параметра. Требуется найти такие значения этого параметра, чтобы полученная зависимость (модель) наилучшим образом описывала имеющиеся экспериментальные данные.

Рассмотрим геометрическую интерпретацию этого вопроса. Перенесём имеющийся набор экспериментальных точек на плоскость, и, тем самым, построим корреляционное поле. Нам необходимо провести линию, которая наилучшим образом отображает закон размещения опытных точек. Эта линия должна проходить как можно ближе по отношению ко всем точкам корреляционного поля. Называют её линией регрессии.

Вид регрессии, которую использует исследователь для наилучшего описания полученных экспериментальных данных, зависит от вида корреляционного поля. Можно использовать экспоненциальную, линейную, логарифмическую, полиномиальную (с произвольной степенью) или степенную функцию для наилучшего описания возможной статистической зависимости.

48

Y

Yi

0

Xi

X

Рис. 4. Корреляционное поле с линией регрессии.

Например, в простой линейной регрессии предполагается, что зависимая переменная y является линейной функцией y = a x + b от независимой переменной x. Требуется найти значения параметров a и b, при которых прямая a x + b будет наилучшим образом описывать (аппроксимировать) экспериментальные точки (x1, y1), (x2, y2), …, (xn, yn). Для поиска параметров обычно используют метод наименьших квадратов – ищут такие значения параметров, чтобы сумма по всем экспериментальным точкам квадратов расстояний (по вертикали) от них до построенной зависимости была минимальной.

Используя один из математических методов, было доказано, что коэффициенты регрессии вычисляются по формулам:

n∑n

xi yi −∑n

xi ∑n

yi

∑n

xi2 ∑n

yi −∑n

xi ∑n

xi yi

a = i=1

i=1

i=1

b = i=1

i=1

i=1

i=1

(22)

n

n

2

n

n

2

n∑xi2 −

∑xi

n∑xi2 −

∑xi

i=1

i=1

i=1

i=1

где xi и yi - элементы выборок (i=1,...,n).

Можно использовать полиномиальную регрессию, в которой предполагается, что зависимая переменная является полиномом некоторой степени от независимой переменной (напомним, что линейная зависимость является полиномом первой степени). Например, полиномом второй степени будет зависимость вида y = a x2 + b x + c и задачей регрессии будет нахождение коэффициентов a, b и c.

Регрессионный анализ, помимо того, что он позволяет количественно описывать зависимость между переменными, дает возможность прогнозировать значения зависимых переменных – подставляя в найденную формулу значения независимых переменных, можно получать прогноз значений зависимых.

49

При этом следует помнить, что построенная модель «локальна», то есть, получена для некоторых вполне конкретных значений переменных. Экстраполяция (распространение) результатов модели на более широкие области значений переменных может привести к ошибочным выводам. Например, если моделировать эндотоксикоз путем повреждения ткани поджелудочной железы, то к токсическому компоненту присоединится банальный протеолитический компонент от ферментов разрушающейся железы. Соответствующие крайне высокие значения прогнозироваться данной моделью на основе регрессионного анализа, естественно, не будут. При хроническом токсическом процессе необратимые изменения в печени и почках по-иному будут воздействовать на формирование результатов, занижая значения показателя, предсказанные формулой регрессии.

Задание №4.

Имеются данные измерений роста X (см) и веса Y (кг) новорождённых:

Xi	50	49	51	48	51	52	50	52	53	50	54	51	55	53	52
Yi	3,2	2,9	3,3	2,6	3,1	3,5	3,0	3,7	3,8	3,4	4,1	3,5	4,0	3,7	3,6

Проведите регрессионный анализ: составьте уравнение линейной регрессии и таблицу наилучшего соответствия веса для роста: 50, 51 и 52 см. Оцените вес ребенка ростом 55 см.

Пример выполнения задания № 4.

1. Вводим исходные данные. Не забываем дать имя файлу, и периодически его сохранять.

50