2. Общие условия устойчивости систем по виду корней характеристического уравнения

Условия устойчивости выражаются в виде различных критериев устойчивости, каждый из которых применяют в зависимости от того, какими исходными характеристиками и данными располагают.

Для САР второго порядка – устойчивость оценивать по корням характеристического уравнения, 3-ого порядка – по критерию Вишнеградского, 4-ого порядка по критерию Гурвица, 5-ого порядка по критерию Михайлова.

В рамках данной работы рассматриваются общие условия устойчивости систем по виду корней характеристического уравнения

2.1 Исследование устойчивости сар по виду корней характеристического уравнения

Для того чтобы стационарная линейная САР, описываемая обыкновенными дифференциальными уравнениями, была устойчивой, необходимо и достаточно, чтобы все корни соответствующего характеристического уравнения имели отрицательные действительные части (тогда САР асимптотически устойчива) [10, 11, 12].

Определены различные критерии (условия), позволяющие судить о знаках корней характеристического уравнения, не решая это уравнение – непосредственно по его коэффициентам. При анализе устойчивости систем, описываемых дифференциальными уравнениями невысокого порядка (до 4-го), пользуются критериями Рауса и Гурвица (Э. Раус, англ. механик; А. Гурвиц, нем. математик) [13,18].

Устойчивость системы связана с характером ее собственных колебаний. Допустим, система описывается следующим дифференциальным уравнением

тогда после преобразования Лапласа получим:

,

где g(p) – входное воздействие.

Устойчивая система вернется в состояние покоя, если входное воздействие равно нулю: g(p) 0 . Следовательно, для устойчивой системы решение однородного дифференциального уравнения

 должно стремиться к нулю при.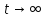

Если найдены корни p₁, p₂, ... , p_nхарактеристического уравнения, то решение однородного уравнения запишется в виде.

Определим условия устойчивости САР.

Предположим, что p_k= a_k– действительный корень.

Этому корню соответствует слагаемое ck. При  ak < 0 ckбудет стремиться к нулю, если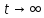. Если же a_k> 0, то x(t), когда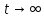. В том случае, когда a_k= 0, это слагаемое не изменяется  и при t стремящемся к бесконечности,

Предположим теперь, что – комплексный корень характеристического  уравнения. Заметим, что в этом случаетакже будет корнем характеристического уравнения. Двум комплексно-сопряженным корням  будут  соответствовать слагаемые видаи.

При этом, если a_k< 0, то в системе имеются затухающие колебания. При a_k> 0 –  колебания возрастающей амплитуды, а при a_k= 0 -колебания с постоянной амплитудой сk.

Можно сделать вывод, система устойчива, если действительные части всех корней характеристического уравнения отрицательны.Если хотя бы один корень имеет действительную часть a_k>0, то система неустойчива. Говорят, что система находится на границе устойчивости, если хотя бы один корень характеристического уравнения имеет нулевую действительную часть, а действительные части всех остальных корней отрицательны.

Это определение хорошо иллюстрируется геометрически. Представим корни характеристического уравнения  точками на комплексной плоскости (рисунок 2).

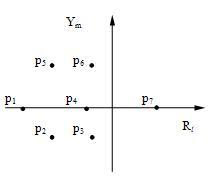
Рисунок 3 - Корни характеристического уравнения  точками на комплексной плоскости

Если все корни лежат в левой полуплоскости комплексного переменного, то система является устойчивой. Если хотя бы один корень лежит в правой полуплоскости комплексного переменного - система является неустойчивой. Если же корни находятся на мнимой оси и в левой полуплоскости, то система находится  на границе устойчивости.

Другими словами, исследование устойчивости САР по виду корней характеристического уравнения основано на определении корней характеристического уравнения, которое записывается из определителя:

.

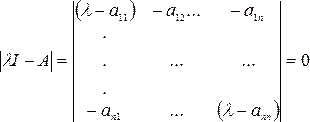Характеристическое уравнение n-го порядка имеет вид

.

Корни характеристического уравнения могут быть вещественными, комплексными или чисто мнимыми. Здесь укажем, что переходная составляющая регулируемого процесса может быть определена только корнями характеристического уравнения:

,

где ,, …,– постоянные интегрирования, которые определяются из начальных условий,,, …,– корни характеристического уравнения.

Рассмотрим вид переходного процесса для случая одного или двух корней характеристического уравнения:

а) вещественные корни характеристического уравнения р1.

- ,.

Процесс будет затухающим при. Система является устойчивой.

- ,.

Процесс будет расходящимся при. Система является неустойчивой (рисунок 3).

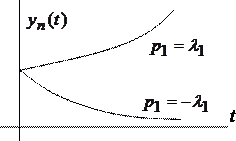
Рисунок 4 – Вид переходного процесса при разных знаках вещественных корней характеристического уравнения

б) комплексные корни характеристического уравнения. Данные корни обычно попарно сопряженные.

.

В этом случае переходный процесс будет определяться выражением

,

где , – новые постоянные времени (рисунок 4).

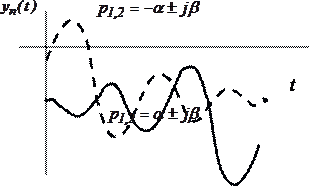
Рисунок 5 – Вид переходного процесса при комплексных корнях характеристического уравнения

 

Переходный процесс  будет затухающим с круговой частотой и показателем затухания. Система устойчива.

.

Переходный процесс будет расходящимся. Система неустойчива.

в) Чисто мнимые корни характеристического уравнения.

,

Переходный процесс определяется выражением (рисунок 5)

.

Процесс представляет незатухающие колебания. Система с точки зрения ее работоспособности может представляться устойчивой или неустойчивой.

Условия устойчивости системы записываются следующим образом:

-  если корни характеристического уравнения имеют отрицательные вещественные части, то система асимптотически устойчива;

-  если среди корней характеристического уравнения имеется хотя бы один с положительной вещественной частью, то система неустойчива;

-  если характеристическое уравнение не имеет корней с положительной вещественной частью, но имеется часть корней с нулевой вещественной частью, то система будет устойчивой.

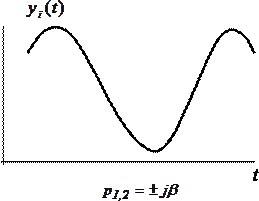
Рисунок 6 – Вид переходного процесса при мнимых корнях характеристического уравнения

Исходя из данных условий, мнимая ось представляет собой граничную линию в плоскости корней, за которую не должны переходить корни характеристического уравнения (рисунок 6).

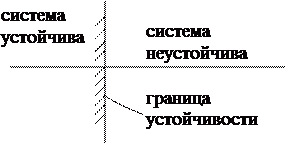
Рисунок 7 – Графическое распределение корней характеристического уравнения

Система будет находиться на границе устойчивости при наличии:

1) нулевого корня;

2) пары чисто мнимых корней;

3) бесконечного корня.

Таким образом, вопрос об устойчивости системы, представленной линейным дифференциальным уравнением, сводится к исследованию корней характеристического уравнения. Однако использование данного подхода представляет значительные трудности для систем выше четвертого порядка, так как корни уравнений не выражаются аналитически через коэффициенты уравнений.