Вопрос 1. Арифметика целых чисел.

На каждом шаге переменные r1, r2 и r используются так же, как в алгоритме Евклида. Переменным r1 и r2 присваиваются начальные значения a и b соответственно. Переменным s1 и s2 присваиваются начальные значения 1 и 0 соответственно. Переменным t1 и t2 присваиваются начальные значения 0 и 1, соответственно. Вычисления r, s и t одинаковы, но с одним отличием. Хотя r — остаток от деления r1 на r2, такого соответствия в других двух группах вычислений нет. Есть только одно частное, q, которое вычисляется как r1/r2 и используется для других двух вычислений.

Вопрос 1. Арифметика целых чисел.

Пример расширенного алгоритма Евклида показан ниже.

Дано a = 161 и b = 28, надо найти НОД (a, b) и значения s и t удовлетворяющие условию: s * a + t * b = НОД (a, b)

Решение:

r = r1 – q x r2 s = s1 – qs2 t = t1 – q x t2

Для отображения алгоритма мы используем следующую таблицу:

q	R1	R2	r	s1	s2	s	t1	t2	t
5	161	28	21	1	0	1	0	1	-5
1	28	21	7	0	1	-1	1	-5	6
3	21	7	0	1	-1	4	-5	6	-23

Мы получаем НОД (161, 28) = 7, s = –1 и t = 6. Найденные значения могут быть проверены по заданному условию:

(–1) x 161 + 6 x 28 = 7

Вопрос 2. Модульная арифметика.

В криптографии мы имеем дело с очень большими целыми числами, настолько большими, что результат их сложения (умножения) не может быть отображен на экране монитора в компьютере. Однако применение ниже рассматриваемых операторов и их свойств позволяет уменьшить разрядность операндов прежде, чем выполнить операцию или оператор. Выполнить такие преобразования помогут операции по модулю и операции сравнения.

Вопрос 2. Модульная арифметика.

Операции по модулю.

Уравнение деления вида (a = n*q + r ), рассмотренное выше, имеет два входа ( a и n ) и два выхода ( q и r ).

В модульной арифметике мы интересуемся только одним из выходов - остатком r. Мы не заботимся о частном q. Такой подход реализует бинарный оператор - оператором по модулю, который обозначается как mod. Следующая схема показывает сравнение операций деления и оператора по модулю.

Второй вход (n ) назван модулем. Выход (остаток) r назван вычетом. В соответствии со схемой, оператор по модулю (mod) выбирает целое число (a) из множества Z и положительный модуль ( n ). Оператор определяет неотрицательный остаток ( r ).

Мы можем сказать, что a mod n = r.

Вопрос 2. Модульная арифметика.

Пример. (функция =ОСТАТ () в Excel) Найти результат следующих операций:

a.27 mod 5

b.36 mod 12

c.–18 mod 14

d.–7 mod 10 Решение

Мы ищем вычет r. Мы должны разделить a на n и найти q и r. Далее нужно игнорировать q и сохранить r.

а. Разделим 27 на 5 - результат: r = 2. Это означает, что 27 mod 5 = 2 Проверка: 27=(5*5)+2

б. Разделим 36 на 12 — результат: r = 0. Это означает, что 36 mod 12 = 0 Проверка: 36=(3*12)+0

в. Разделим (–18) на 14 — результат: r = –4. Однако мы должны прибавить модуль (14), чтобы сделать остаток неотрицательным. Мы имеем r = –4 + 14 = 10. Это означает, что –18 mod 14 = 10.

-18=(-1*14)+(-4)=(-2*14)+14-4=(-2*14)+10 (см.слайд 6)

г.Разделим (–7) на 10 — результат: r = –7. После добавления модуля

к–7 мы имеем r = 3. Это означает, что –7 mod 10 = 3.

Проверка: -7=(-1*10)+3

q= q1+t, т.е. a Ξ b(mod m).

Операции сравнения.

Если двум целым а и b отвечает один и тот же остаток r, то они называются сравнимыми по модулю m.

Сравнимость чисел а и b по модулю т записывается так: a Ξ b(mod m),

или так: а сравнимо с b по модулю m

Сравнимость чисел а и b по модулю m равносильна:

1) возможности представить а в виде а = b+mt, где t — целое;

2) делимости а — b на m. Действительно, из a Ξ b(mod m) следует

a=mq+r, b= mq1 + r; 0 ≤ r< m, откуда a-b=m(q- q1 ), а = b+mt, t= q- q1. обратно, из а = b+mt,

представляя b в виде b = mq1 + r, 0≤ r<m, выводим

a=mq+r;

Вопрос 2. Модульная арифметика.

Результат операции по модулю n — всегда целое число между 0 и n. Операция по модулю n создает набор, который называется множеством вычетов по модулю n, или Zn.

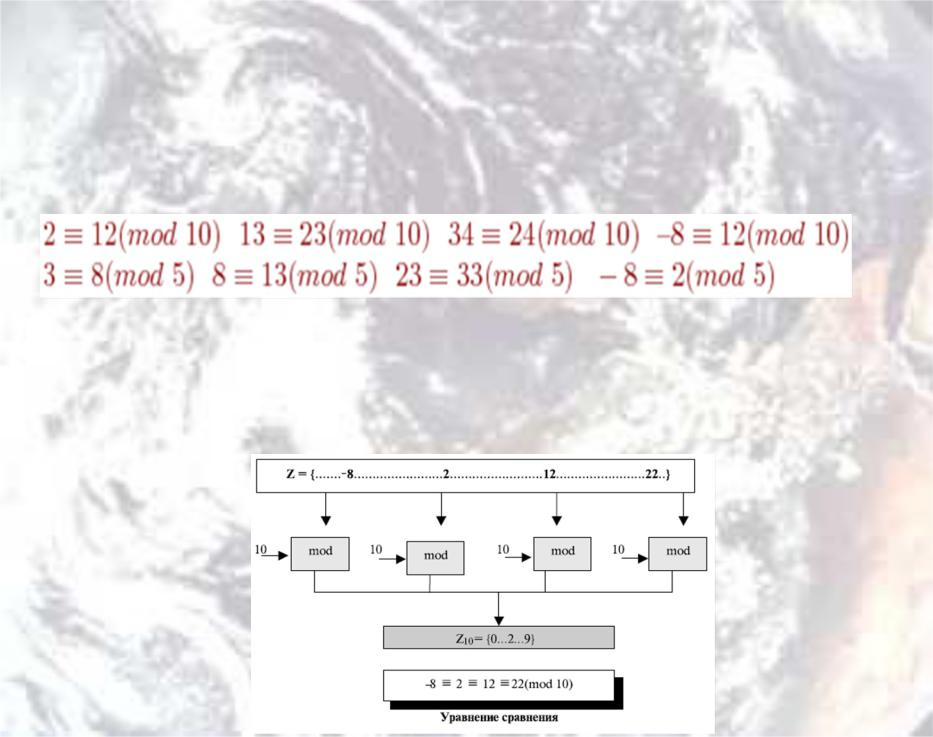
Примеры результатов сравнения по модулю 10 и 5:

Например, результат 2 mod 10 = 2, 12 mod 10 = 2, 22 mod 10 = 2, и так далее. В модульной арифметике целые числа -8, 2, 12, и 22, называются сравнимыми по модулю 10 (mod 10).

На следующей схеме показан принцип данного сравнения:

Вопрос 2. Модульная арифметика.

1.Оператор сравнения напоминает оператор равенства, но между ними есть различия.

Первое: оператор равенства отображает элемент множества Z на элемент множества Z; оператор сравнения отображает элемент множества Z на элемент множества Zn.

Второе: оператор равенства показывает, что наборы слева и справа соответствуют друг другу "один в один", оператор сравнения — "многие

—одному".

2.Обозначение (mod n ), которое мы вставляем с правой стороны оператора сравнения, обозначает признак множества ( Zn ). Мы должны добавить это обозначение, чтобы показать, какой модуль используется в отображении.

Обозначение mod в операторе сравнения и операторе по модулю принципиально отличаются:

Символ mod в выражении 12 mod 10 — оператор; (mod 10) в операторе сравнения — набор Z10.

Система вычетов Zn

Другими словами, это набор всех целых чисел, таких, что x = a (mod n). Например, если n = 5, мы имеем множество из пяти элементов [0], [1], [2], [3] и [4], таких как это показано ниже:

[0]= {…., –15, –10, –5, 0, 5, 10, 15, …}

[1]= {…., –14, –9, –4, 1, 6 , 11, 16,…}

[2] = {…., –13,	–8, –3, 2, 7, 12, 17,…}
[3] = {...., –12,	–7, –2, 3,	8,	13, 18,…}
[4] = {…., –11,	–6, –1, 4,	9,	14, 19,…}

Целые числа в наборе [0] все дают остаток 0 при делении на 5 (сравнимы по модулю 5 ). Целые числа в наборе [1] все дают остаток 1 при делении на 5 (сравнимы по модулю 5 ), и так далее.

В каждом наборе есть один элемент, называемый наименьшим (неотрицательным) вычетом. В наборе [0] это элемент 0 ; в наборе [1] — 1, и так далее. Набор, который показывает все наименьшие вычеты: Z5 = {0, 1, 2, 3, 4}. называется набором всех наименьших вычетов по модулю n.

Вопрос 2. Модульная арифметика.

Операции в системе вычетов

Три бинарных операции ( сложение, вычитание и умножение могут быть определены для набора Zn (системы вычетов). Результат данных операций в Zn определяется с использованием операции по модулю, как это показано на рисунке.

Фактически применяются два набора операторов: бинарных и оператора по модулю. Чтобы подчеркнуть порядок вычислений используются круглые скобки. Как показано на рисунке, входы ( a и b ) могут быть членами Z или Zn.

	Вопрос 2. Модульная арифметика.
Примеры операторов в Zn
а. Сложение 7 и 14 в Z15	(14+7) mod 15 -> (21) mod 15 = 6
б. Вычитание 11 из 7 в Z13	(7–11) mod 13 -> (-4) mod 13 = 9
в. Умножение 11 на 7 в Z20	(7x11) mod 20 -> (77) mod 20 = 17

Свойства оператора mod

Первое свойство: (a + b) mod n = [(a mod n) + (b mod n)] mod n Второе свойство: (a – b) mod n = [(a mod n) - (b mod n)] mod n Третье свойство: (a x b) mod n = [(a mod n) x (b mod n)] mod n

10n mod x = (10 mod x)n

Применение третьего свойства n раз.

10 mod 3 = 1 -> 10n mod 3 = (10 mod 3)n = 1 10 mod 9 = 1 -> 10n mod 9 = (10 mod 9)n = 1

10 mod 7 = 3 -> 10n mod 7 = (10 mod 7)n = 3n mod 7