Математика

	3n 1 2n		2n 1
99.		100.
	n!		n 1 !
n 1		n 1
					n		x	n
В задачах 101–120 дан степенной ряд				a					. При заданных
			n 1 kn b

значениях a ,b ,k, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.

101.	a=2;	b=3;	k=4.	102.	a=7;	b=5;	k=4.
103.	a=3;	b=4;	k=1.	104.	a=5;	b=7;	k=4.
105.	a=4;	b=3;	k=3.	106.	a=3;	b=8;	k=1.
107.	a=5;	b=6;	k=2	108.	a=4;	b=7;	k=3.
109.	a=3;	b=7;	k=3	100.	a=3;	b=5;	k=3.
111.	a=6;	b=5;	k=3.	112.	a=4;	b=5;	k=3.
113.	a=5;	b=2;	k=1.	114.	a=6;	b=7;	k=1.
115.	a=2;	b=3;	k=5.	116.	a=5;	b=8;	k=2.
117.	a=3;	b=5;	k=6.	118.	a=8;	b=3;	k=4.
119.	a=2;	b=7;	k=1.	120.	a=9;	b=2;	k=1.

В задачах 121–140 вычислить определенный интеграл с точностью до 0,001.

	0,5 ln(1 x2 )
121.														dx
								x
	0
	0,2 e x 1
123.										dx
							x
	0
	0,5					dx
125.												.
			3 1 x3
	0
	1	sin			x
127.								dx .
	0				x
	0,5
129.				1 x3 dx .
	0

1

131. xsin xdx .

0

0,5

122. e 4 x2 dx .

		0
		1
	124. cos					xdx .
		0
		0,1
	126.	cos(10x2 )dx .
		0
		0,5
	128.	cos(2x2 )dx .
		0
		0,3
	130.	e 2 x2 dx .
		0
		0,5		dx
	132.								.
			3 1		x2
		0

60

0,4

133. e 5 x2 dx .

0

1

135. x cos 3 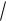xdx .

0 0,2

137. cos(x2 )dx .

0
0,1			x)
139.	ln(1			dx .
0		x

61

	134.	0,5			sin 4x							dx .
		0							x
		0,2				1 e x
	136.													dx .
										x
		0
		1							dx
	138.													.
			3				1 x4
		0
	140.	0,5		sin					x		dx .
				3
		0							x

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

12 СЛУЧАЙНЫЕ СОБЫТИЯ

Пример 40. В корзине 12 яблок, из них 5 поражены болезнью в скрытой форме. Наудачу берут последовательно 3 яблока. Какова вероятность, что все 3 яблока окажутся больными, если после проверки яблоки в корзину не возвращались?

Решение. 1 способ. Введем элементарные события А1 – первое взятое яблоко оказалось больным, А2 – второе взятое яблоко оказалось больным, А3 – третье взятое яблоко оказалось больным. Событие А – все три взятых яблока оказались больными:

АА1 А2 А3 .

Вданной ситуации события А1, А2 , А3 – зависимые, так как яблоки в

корзину не возвращались. Тогда

Ð( À ) Ð( À1 À2 À3 ) Ð( À1 ) ÐÀ1 ( À2 ) ÐÀ1 À2 ( À3 ) 125 114 103 221 .

Пример 41. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным равно 0,1. Проверено три изделия. Какова вероятность того, что два из них бракованные?

Решение. Введём события: бракованная деталь – событие А, небракованная деталь – событие А , две детали из трех небракованные – В.

По условию P( A) 0,1; P( A) 0,9.

Если среди трех деталей оказывается две бракованных, то это возможно в одном из трех случаев: небракованная деталь будет первой, второй или третьей. Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим:

P В P( A)P( A)P( A) P( A)P( A)P( A) P( A)P( A)P( A)

P В 3 0,1 0,1 0,9 0,027.

Пример 42. На сборку телевизоров поступают микросхемы от двух поставщиков, причем 70% микросхем от первого поставщика, 30% – от второго. Брак микросхем первого поставщика составляет 2%, второго – 3%.

62

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1)Какова вероятность, что взятая наудачу микросхема окажется бракованной?

2)Взятая наудачу микросхема оказалась бракованной. Какова вероятность, что микросхема изготовлена первым поставщиком? вторым поставщиком?

Решение. 1) Обозначим Н1 – взятая наудачу микросхема изготовлена первым поставщи-

ком,

Н 2 – взятая наудачу микросхема изготовлена вторым поставщиком,

А – взятая наудачу микросхема дефектная.

Тогда А Н1 А Н2 А. По условию имеем

Р(Н1) 0,7; Р(Н2 ) 0,3;

Сделаем проверку: Р(Н1) Р(Н2 ) 0,7 0,3 1 (верно). Из условия задачи следует, что

РН1 ( А) 0,02; РН2 ( А) 0,03.

Тогда по формуле полной вероятности

Р( А) Р(Н1) РН1 ( А) Р(Н2 ) РН2 ( А) 0,7 0,02 0,3 0,03 0,023 .

2) Пусть событие А – взятая наудачу микросхема дефектна – произошло в результате испытания. Найдем вероятность того, что эта микросхема была изготовлена первым поставщиком по формуле Байеса:

РA (H1)	Р(Н1) РН		( А)			0,7 0,02			0,61.
	1
		P( A)					0,023
Аналогично, вероятность того, что микросхема была изготовле-
на вторым поставщиком:
РA (H2 )		Р(Н2 ) РН ( А)					0,3 0,03		0,39 .
			2
		P( A)					0,023

Сделаем проверку: РА (Н1) РА (Н2 ) 0,61 0,39 1 (верно). Как видим, произошла «переоценка» вероятностей гипотез по-

сле факта наступления события А:

Р(Н1) 0,7; а РА (Н1) 0,61; Р(Н2 ) 0,3; а РА (Н2 ) 0,39 .

Пример 43. По самолету производится 3 выстрела с вероятностями попадания 0,5; 0,6; 0,8. Для вывода самолета из строя заведомо

63

достаточно трех попаданий; при одном попадании самолет выходит из строя с вероятностью 0,3; при двух попаданиях – с вероятностью 0,6. Найти вероятность того, что в результате трех выстрелов самолет будет сбит.

Решение. Введем событие В – в результате трех выстрелов самолет сбит. Гипотезы:

Í 0 – в результате трех выстрелов не произошло ни одного попадания;

Í1 – в результате трех выстрелов произошло одно попадание;

Í2 – в результате трех выстрелов произошло два попадания;

Í3 – в результате трех выстрелов произошло три попадания.

Тогда В Н0 В Н1 В Н2 В Н3 В , Р(В) Р(Н0 ) РН0 (В) Р(Н1) РН1 (В) Р(Н2 ) РН2 (В) Р(Н3 ) РН3 (В) .

Найдем вероятности гипотез:

Р(Н0 ) 0,5 0,4 0,2 0,04, Р(Н1) 0,5 0,4 0,2 0,5 0,6 0,2 0,5 0,4 0,8 0,26,

Р(Н2 ) 0,5 0,6 0,2 0,5 0,4 0,8 0,5 0,6 0,8 0,46,

Р(Н3 ) 0,5 0,6 0,8 0,24 ,
Условные вероятности появления события В:
РН (В) 0 ;	РН (В) 0,3;	РН (В) 0,6 ;	РН (В) 1.
0	1	2	3

В итоге имеем

Р(В) 0,04 0 0,26 0,3 0,46 0,6 0,24 1 0,594 .

Контрольные вопросы

1.Что называется суммой двух событий?

2.Что называется произведением двух событий?

3.Какие события в данном испытании называются несовместными? совместными?

4.Сформулируйте теорему сложения вероятностей совместных событий и теорему сложения вероятностей несовместных событий.

5.Какие события называются зависимыми? независимыми?

6.Какая вероятность события В называется условной?

7.Сформулируйте теорему умножения вероятностей зависимых событий и теорему умножения вероятностей независимых событий.

8.Какие события образуют полную группу?

9.Какие события называются противоположными?

10.Чему равна сумма вероятностей противоположных событий?

64

11.Какой вид имеет формула полной вероятности? Что определяется по формуле полной вероятности?

12.Какой вид имеет формула Байеса? Что определяется по формуле Байеса?

13.По какой формуле подсчитывается вероятность появления события хотя бы один раз?

65

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

13 ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ

Пример 44. Вероятность всхожести семян пшеницы равна 0,9. Какова вероятность того, что из четырех посеянных семян взойдут не менее трех?

Решение. Пусть событие А – из 4 семян взойдут не менее 3 семян; событие В – из 4 семян взойдут 3 семени; событие С – из 4 семян взойдут 4 семени. По теореме сложения вероятностей несовместных событий

Р(А) Р(В) Р(С) .

Вероятности Ð( Â ) и Ð( Ñ ) определим по формуле Бернулли, применяемой в следующем случае. Пусть проводится серия из п независимых испытаний, в каждом из которых вероятность наступления события постоянна и равна р, а вероятность ненаступления этого события равна q 1 p . Тогда вероятность того, что событие А в п испытаниях появится ровно k раз, вычисляется по формуле Бернулли

			P (k) C k pk qn k ,
			n		n
где C k	n!		– число сочетаний из п элементов по k . Тогда
n	k!(n k)!
P(B) P (3) C3 p3q4 3					4!			0,93 (1	0,9)	0,2916;
	4		4		3!(4 3)!
P(C) P (4) C 4 p4q4 4				0,94		0,6561.
	4		4

Искомая вероятность

P(A) 0,2916 0,6561 0,9477.

Пример 45. Дана вероятность р=0,9 того, что семя люцерны прорастет. Найти вероятность того, что из п=100 посеянных семян прорастет ровно k = 80 семян.

Решение. Так как п – велико, то применяем локальную формулу Муавра-Лапласа:

1

k np

1

е

х2

P (k)

(x) ,

где x

, (х)

2

n

n p q

n p q

2

1) x	80 100 0,9					10		3,33 .
		100 0,9 0,1				3

2) (х) – четная функция, ( 3,33) (3,33).

66

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Находим по таблице (3,33) 0,0016 .

3) Тогда	P (80)			1			0,0016 0,0005 .
	100	100		0,9	0,1

Так как полученная вероятность очень мала, то событие, что из 100 семян взойдет ровно 80, практически невозможно.

Пример 46. Дана вероятность р=0,8 правильного разбиения участка в каждом из 100 независимых испытаний. Найти вероятность того, что в этих испытаниях правильное разбиение участка произой-

дёт не менее 72 и не более 84 раз.
Решение. Дано: р=0,8, n=100, k1 =72, k2 =84.
Так как n 100 – велико, а																72 k 84; 0,1 p 0,9 , то применя-
ем интегральную формулу Лапласа:
Pn (k1 k k2 ) Ф(x2 ) Ф(x1) ,																			1				e 2	dt; q 1 p
где x1 k1 np ; x2 k2										np ; Ф(x)
																							x t	2
																						0
				npq						npq										2
Вычислим значения x1										и x2
x	72 0,8 100							2; х							84 0,8 100								1,
											2
1	100 0,8 0,2															100 0,8			0,2

Находим значение функции Ф(x) по таблице

Ф(x1) Ф(-2) Ф(2) 0.4772 Ф(x2 ) Ф(1) 0.3413

Получим

P ( 72 k 84 ) Ô(1) Ô( 2 ) 0.3413 0.4772 0,8185.

100

Ответ: 0,8185.

Пример 47. Дана вероятность р отказа одного элемента в течение часа. Устройство состоит из n элементов работающих независимо друг от друга. Найти вероятность того, что за час откажут не более m элементов.

Дано: р=0,001, n=500, m=1.

Решение. Так как по условию задачи число испытаний n 500 – велико, а вероятность отказа каждого элемента p 0,001 – мала ( p 0,1), то для нахождения искомой вероятности применяем формулу Пуассона:

67

P ( m )	m
	e ; np
n	m!
Находим 500 0,001 0.5
P (1)	0.51	e 0.5	0.5			0,226
500	1!			e

Ответ: 0,226

Контрольные вопросы

1.Какие испытания называются независимыми по отношению к событию А?

2.Какой вид имеет формула Бернулли? Что означают p, q, n, k, Pn (k) ?

3.В каких случаях целесообразно применять формулу Бернулли?

4.По каким формулам вычисляется вероятность появления события не менее k раз?

5.Что называется наивероятнейшим числом появлений события А в n независимых испытаниях?

6.По какой формуле вычисляется наивероятнейшее число появлений события k0 ?

7.Сформулировать локальную теорему Лапласа. В каких случаях она применяется?

8.Какой вид имеет формула Пуассона? В каких случаях она применяется?

9.Сформулировать интегральную теорему Лапласа. В каких случаях она применяется?

10.По какой формуле подсчитывается вероятность отклонения относительной частоты от вероятности появления события в одном испытании?

68

14 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Пример 48. Задан закон распределения дискретной случайной величины Х. Найти: 1) математическое ожидание М ( Х ) ; 2) дисперсию D( X ) ; 3) среднее квадратическое отклонение X .

Х

40

42

41

44

р0,1 0,3 0,2 0,4

Решение. 1) Если закон распределения дискретной случайной величины задан таблицей, где в первой строке даны значения случайной величины Х, а во второй – вероятности этих значений, то математическое ожидание М ( Х ) вычисляется по формуле

n

М ( Х ) х1 р1 х2 р2 ... хп рп хi рi .

i 1

Тогда M (X ) 40 0,1 42 0,3 41 0,2 44 0,4 42,4.

2) Дисперсией D( X ) дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.

n

D( X ) M[ X M ( X )]2 [xi M ( X )]2 pi .

i 1

Эта величина характеризует среднее ожидаемое значение квадрата отклонения Х от М ( Х ) . Из последней формулы имеем

D( X ) (40 42,4)2 0,1 (42 42,4)2 0,3 (41 42,4)2 0,2

(44 42,4)2 0,4 2,42 0,1 0,42 0,3 1,42 0,2 1,62 0,4 2,04.

Дисперсию D( X ) можно найти другим способом, исходя из следующего ее свойства: дисперсия D( X ) равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания М ( Х ) , то есть

D( X ) M ( X 2 ) [M ( X )]2 .

Для вычисления M ( X 2 ) составим следующий закон распределения величины X 2 :

Х2	402	422	412	442
р	0,1	0,3	0,2	0,4

69