ПГСХА Высшая Математика, примеры от 13-03-2013 / НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ новое

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

1. Подведение под знак дифференциала, замена переменной.

2. Метод интегрирования по частям . (1)

1) Интегралы вида P(x)e^kx dx, Р(х) sin kх dx, Р(х) cos kx dx, где Р(х) — многочлен, k — число. Удобно положить u = Р(х), а за dv обозначить все остальные сомножители.

2) Интегралы вида P(x) arcsin x dx, P(x) arccos x dx, Р(х) arctg x dx,P(x) arcctg x dx,P(x) ln x dx. Удобно положить P(x) dx = dv, а за u обозначить остальные сомножители.

3) Интегралы вида е^ах sin bх dx, е^ах cos bх dx, где а и b — числа. За u можно принять функцию u=е^ах, применить интегрирование по частям дважды, составить уравнение относительно искомого интеграла.

3. Интегрирование рациональных дробей.

1) Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби;

2) Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей:

Теорема. Всякую правильную рациональную дробь, знаменатель которой разложен на множители

Q(х) = (х – x₁ (х - х_2....(х- х_r... (2) (корни квадратного трехчлена комплексные), можно представить в виде следующей суммы простейших дробей:

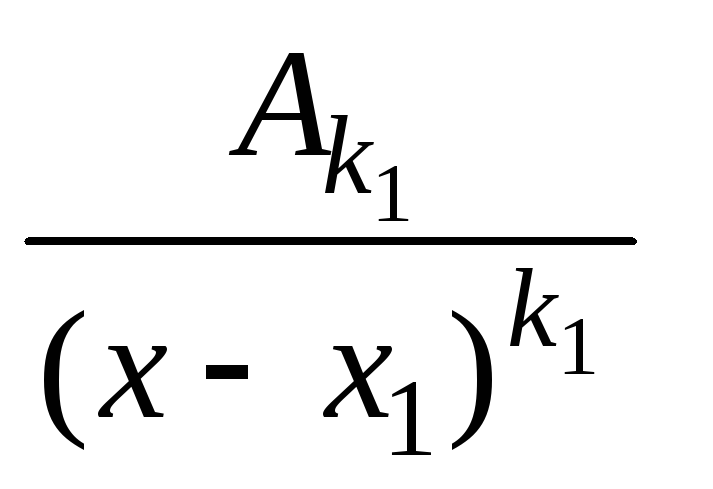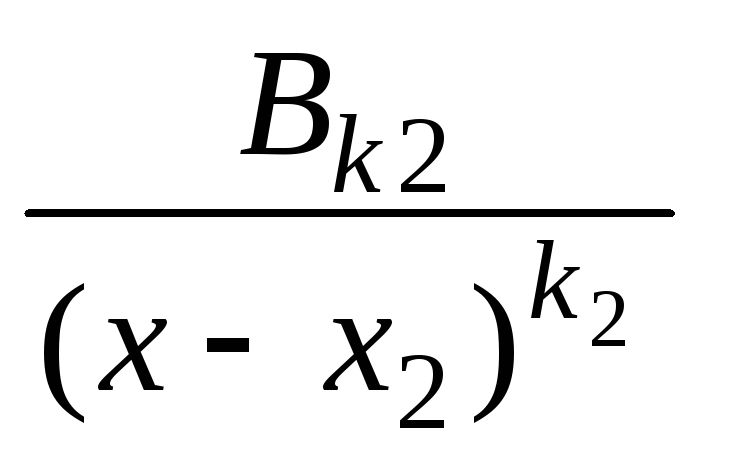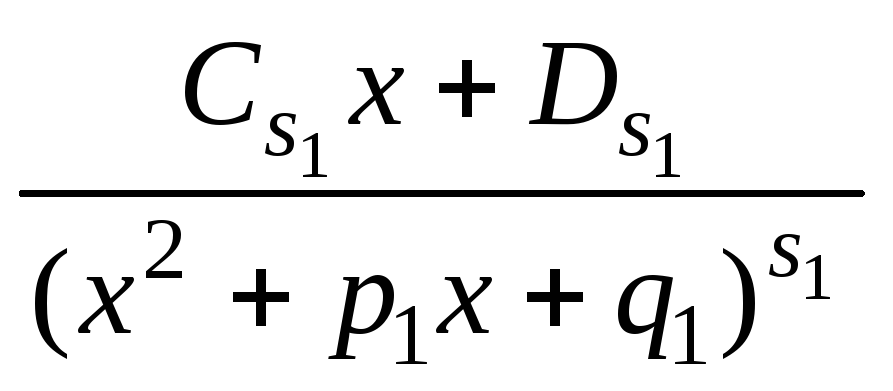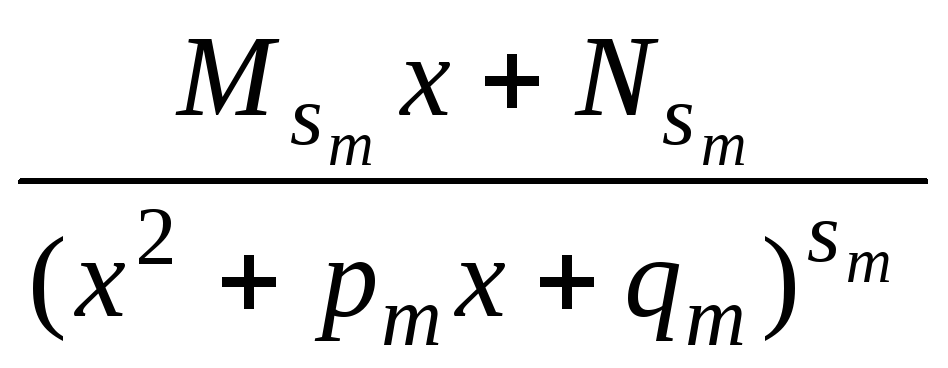=++...++++...++...++ ++...++...+++...+ (3)

Найти неопределенные коэффициенты.

3) Проинтегрировать многочлен и полученную сумму простейших дробей:

Интегрирование простейших рациональных дробей.

1. = A=А · ln |х – а| + С; (4)

2. = A= ; (5)

3. (6) , где знаменатель не имеет действительных корней. В знаменателе выделить полный квадрат, заменить выражение под квадратом новой переменной, разбить на сумму двух интегралов, первый из которых заменой переменной приводится к табличному (№2), второй – к табличному (№15).

4. (7), где знаменатель не имеет действительных корней. В знаменателе выделить полный

квадрат, выполнить подстановку , разбить на сумму двух интегралов, первый из которых решается с помощью замены переменной, второй – с помощью рекуррентной формулы

(8) (9)

4. Интегрирование тригонометрических функций.

1) Универсальная тригонометрическая подстановка tgt, (10) sin x=, cos x=, dx =dt

• если функция R(sin x;cos x) нечетна относительно sin x, т.е. R(— sin x; cos x) = —R(sin x;cos x), то

подстановка cos x = t; (11) , ,

• если функция R(sin x;cos x) нечетна относительно cos x, т.е. R(sin x; —cos x) = —R(sin x;cos x), то

подстановка sin x = t; (12) , ,

• если функция R(sin x;cos x) четна относительно sin x и cos x: R(—sin x; —cos x) =R(sin x;cos x), то

подстановка tg x = t (13) , ,

2) Интегралы типа .

• подстановка sin x = t, если n — целое положительное нечетное число;

• подстановка cos x = t, если m — целое положительное нечетное число;

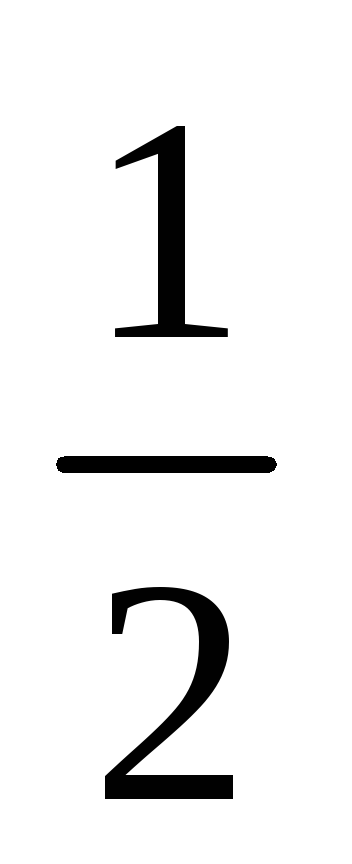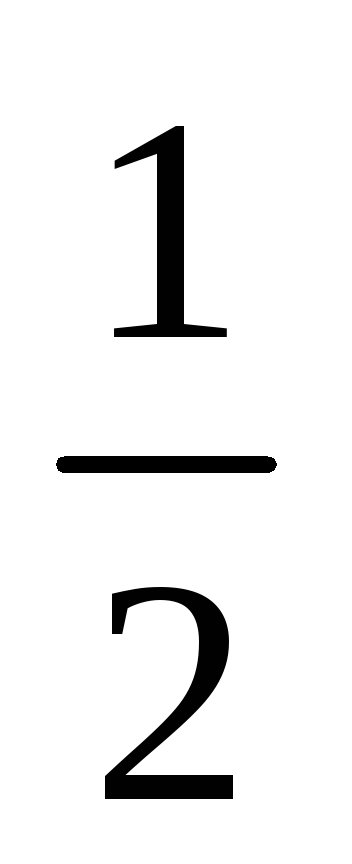• формулы понижения порядка: cos²x = (1 + cos 2x), sin²x = (1 – cos2x), sin x ∙ cos x =sin2x, (14) если m и n — целые неотрицательные четные числа;

• подстановка tg х = t, если т + п — есть четное отрицательное целое число.

3) Использование тригонометрических преобразований. sin α cosβ = (sin(α – β) + sin(α +β)),

cos α cosβ = (cos(α —β) + cos(α +β)), sin α sinβ = (cos(α —β)—cos(α +β)). (15)

5. Интегрирование иррациональных функций.

1) Квадратичные иррациональности., , : под радикалом выделить полный квадрат и сделать подстановку х + = t. (16)

2) Интегралы типа dx, где Р_n(x)—многочлен степени n, можно вычислять, пользуясь формулой

dx = Q_n-1(x)+ (17) где Q_n-1(x) — многочлен степени (n – 1) с неопределенными коэффициентами, — также неопределенный коэффициент. Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих частей равенства (14): . (18)

после чего необходимо приравнять коэффициенты при одинаковых степенях неизвестной х.

3) Дробно-линейная подстановка. Интегралы типа , где a, b, c, d – действительные числа, - натуральные числа, подстановка , (19) где k — наименьшее общее кратное знаменателей дробей .

4) Тригонометрическая подстановка.

Интеграл подстановка (20)

Интеграл подстановка (21)

Интеграл подстановка (22)

5) Интегрирование дифференциального бинома. Интегралы типа , где а, b — действительные числа; т, п, р — рациональные числа.

• если р — целое число, то подстановка х = t^k , (23) где k — наименьшее общее кратное знаменателей дробей m и n;

• если 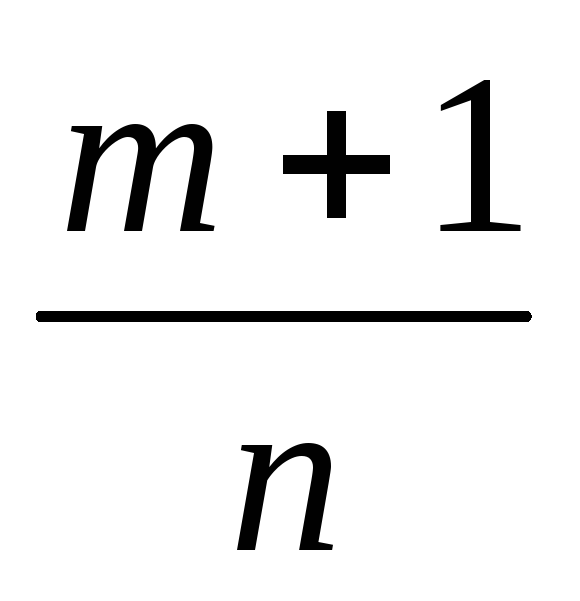— целое число, то подстановка а + bхⁿ = t^s, (24) где s —знаменатель дроби р;

• если + р — целое число, то подстановка а + bхⁿ = хⁿ t^s, (25) где s — знаменатель дроби р.

6. «Неберущиеся» интегралы.

dx — интеграл Пуассона (теория

вероятностей),

интегральный логарифм (теория чисел),

, — интегралы Френеля (физика),

dx, dx — интегральные синус и

косинус,

dx — интегральная показательная функция.