4.3 Знакочередующиеся ряды и знакопеременные ряды

Знакочередующиеся ряды. Признак Лейбница.

Знакочередующимся рядомназывают ряд вида

(4.3.1)

для всех ).

Другими словами: знакочередующийся ряд – ряд, в котором положительные и отрицательные члены ряда следуют друг за другом поочередно.

Теорема 6(признак Лейбница): Знакочередующийся ряд (4.3.1) сходится, если

1. последовательность абсолютных величин членов ряда монотонно убывает, т.е.

(4.3.2)

1. общий член ряда стремится к нулю

(4.3.3)

При этом сумма S ряда (4.3.1) удовлетворяет неравенствам. (4.3.4)

Замечание: теорема Лейбница справедлива, если неравенства (4.3.2) выполняются, начиная с некоторого номера N.

Ряды, для которых выполняются условия (4.3.2) и (4.3.3) называются лейбницевскими.

Соотношение (4.3.4) позволяет получить простую и удобную оценку ошибки, которую допускают, заменяя сумму Sданного ряда его частичной суммой. Отброшенный ряд (остаток) представляет собой также знакочередующийся рядсумма которого по модулю меньше первого члена этого ряда, т.е.. Поэтому ошибка меньше модуля первого из отброшенных членов.

Пример: вычислить приблизительно сумму ряда

Данный ряд лейбницевского типа.

- ряд сходится по признаку Лейбница.

Можно записать

Возьмем пять членов, т.е. заменим Sна, получим

.

Ошибка, которую делаем меньше, чем

Вычислить сумму данного ряда с точностью 0,01.

Знакопеременные ряды. Абсолютная и условная сходимость числовых рядов.

Числовой ряд , содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называетсязнакопеременным.

Теорема(общий достаточный признак сходимости знакопеременных рядов).

Пусть дан знакопеременный ряд.

(4.3.5)

Если сходится ряд

, (4.3.6)

составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

Обратное утверждение несправедливо, если сходится ряд (4.3.5), то это не означает, что будет сходится ряд (4.3.6).

Замечание: из расходимости ряда , расходимость рядавообще не следует.

Но если к ряду применив признак Даламбера (или Коши), получаем

- то в этом случае оба ряда (4.3.5) и (4.3.6) расходятся.

Определение. Знакопеременный ряд называется абсолютно сходящимся, если ряд , составленный из модулей его членов, сходится.

Опр. Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Пример: исследуем сходимость ряда

Ряд знакочередующийся, для которого выполняются условия признака Лейбница.

1. члены ряда убывают по абсолютной величине ;

2) .

Поэтому ряд сходится по признаку Лейбница.

Ряд, составленный из модулей

- является гармоническим, который, как известно, расходится. Т.е. исходный ряд является условно сходящимся.

Основные свойства абсолютно сходящихся рядов:

1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится, и имеет ту же суммуS, что и исходный ряд.

2. Абсолютно сходящиеся ряды с суммами иможно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна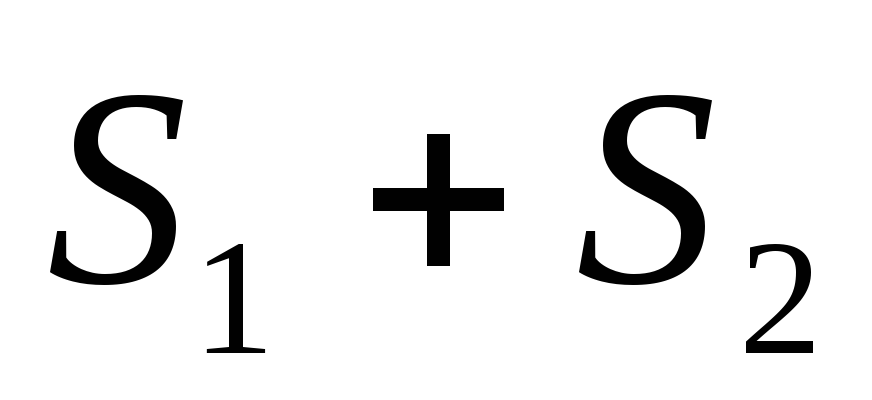(или соответственно)

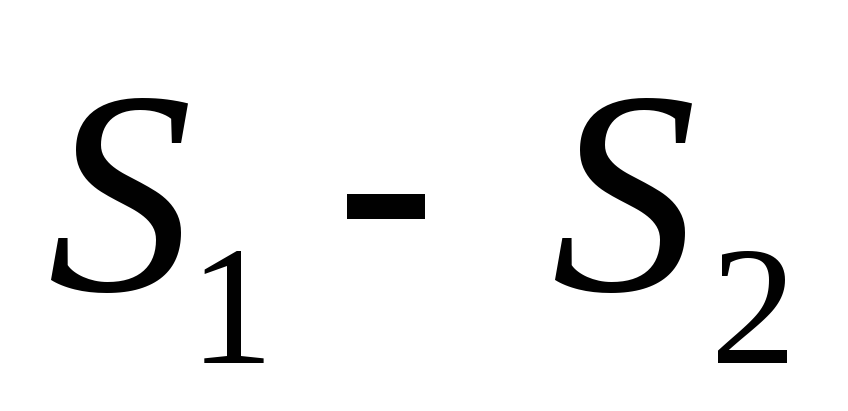3. Произведение двух абсолютно сходящихся рядов с суммами и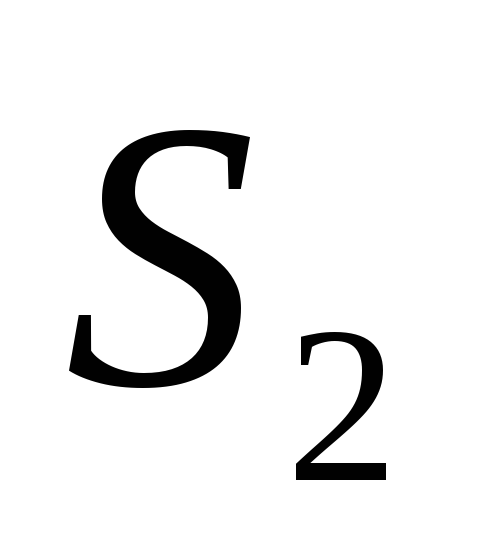есть абсолютно сходящийся ряд, сумма которого равна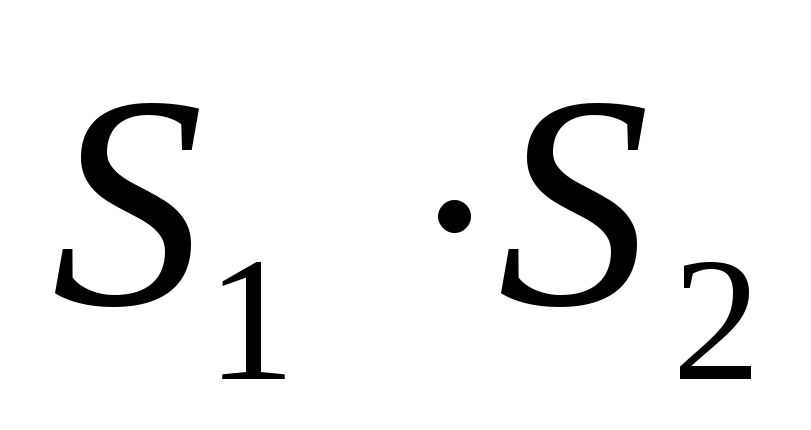(ряды умножаются по правилу умножения многочленов).

4. В случае условно сходящихся рядов эти свойства, вообще говоря, не имеют смысла.

Пример: ряд условно сходится.

Пусть его сумма равна S. Перепишем его члены так, что после одного положительного члена будут идти два отрицательных.

Получим ряд

Сумма уменьшилась вдвое.

Более того, путем перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее заданной суммой или расходящийся ряд.