Вычисление объема тела

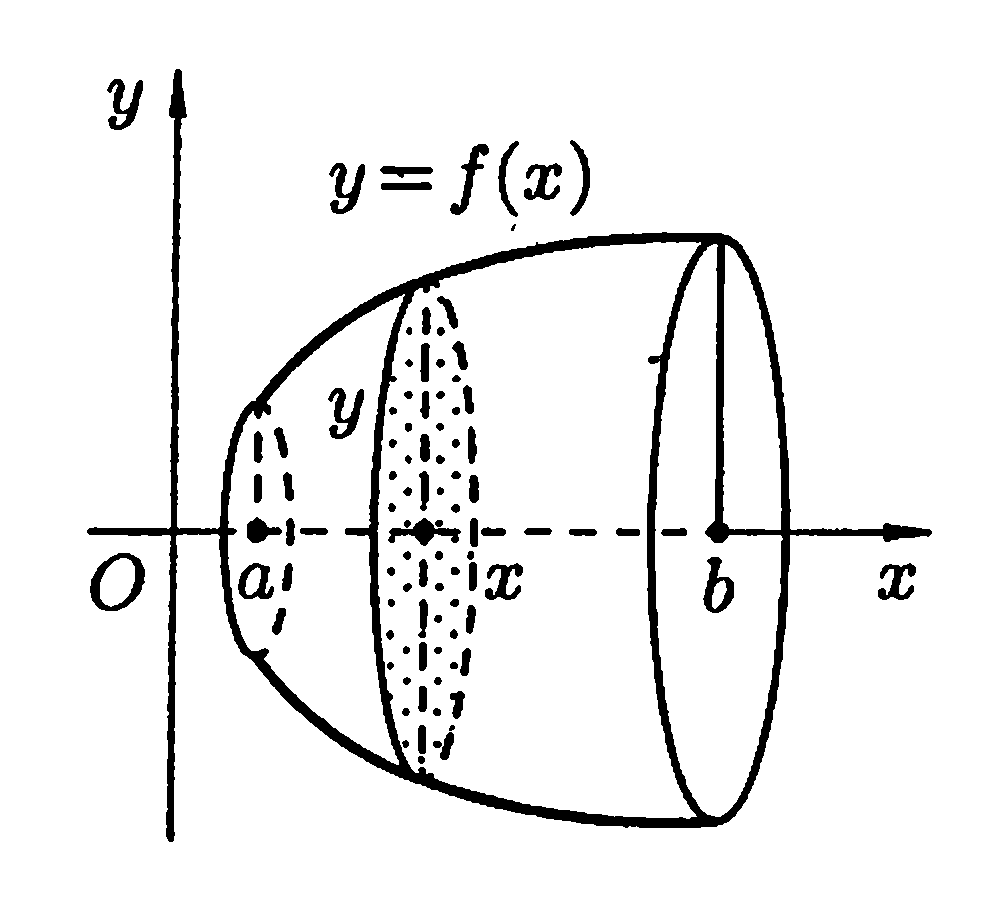
Объем тела, образованного вращением вокруг оси криволинейной трапеции, ограниченной линиями , и прямыми , можно найти по формуле

.

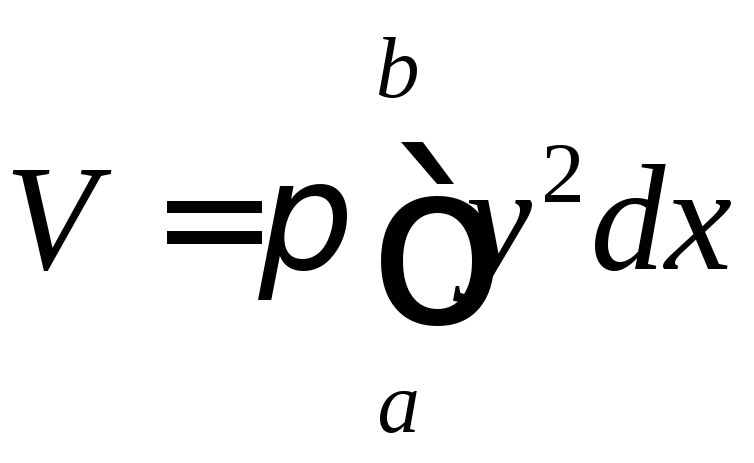● Пример 6. Найти объем тела, образованного вращением фигуры, ограниченной линиями , , вокруг оси .

Решение.

(куб.ед.) ●

Вопросы для самоконтроля

1. Вычисление площадей в декартовых координатах.

2. Вычисление площадей, ограниченных кривыми, заданными параметрически.

3. Площадь криволинейного сектора в полярных координатах.

4. Вычисление объема тела по известным площадям параллельных сечений.

5. Вычисление объема тела вращения.

6. Длина дуги кривой в декартовых координатах.

7. Длина дуги кривой, заданной параметрически.

8. Длина дуги кривой в полярных координатах.

Тема 11 «Дифференциальные уравнения»

Основные понятия

Дифференциальным уравнением называется соотношение, связывающее независимые переменные, их функцию и производные этой функции. Если независимая переменная одна, то дифференциальное уравнение называется обыкновенным дифференциальным уравнением; если же независимых переменных две или больше, то дифференциальное уравнение называется дифференциальным уравнением в частных производных.

В данном кратком курсе ограничимся рассмотрением лишь обыкновенных дифференциальных уравнений.

Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, искомую неизвестную функцию этой переменной и ее (функции) производные различных порядков.

Согласно вышесказанному, в общем виде в неявной форме, обыкновенное дифференциальное уравнение запишется следующим образом:

, (1)

где F – известная функция своих аргументов;

х – независимая переменная;

у – искомая неизвестная функция, зависящая от х;

у^/, у^//….уⁿ – производные по аргументу х искомой функции у.

Порядком дифференциального уравнения называется наивысший порядок производной неизвестной функции, входящей в уравнение.

Например:

1. - обыкновенное дифференциальное уравнение 1-го порядка;

2. - обыкновенное дифференциальное уравнение 3-го порядка;

3. уравнение (1) – общий вид обыкновенного дифференциального уравнения n-го порядка;.

Решением дифференциального уравнения (1) называется всякая n – раз дифференцируемая функция , которая при подстановке в указанное уравнение обратит его в тождество.

Дифференциальное уравнение имеет бесчисленное множество решений.

График функции, являющейся решением дифференциального называется интегральной кривой.

Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения.

Пример 1. Показать, что функция является решением дифференциального уравнения: (2)

при любом .

Решение. Найдем у^/ и у^///:

Подставив полученные выражения для у^/ и у^//\ в уравнение (2), имеем:

Таким образом, получилось тождество , которое имеет место при любом . Следовательно, функция , действительно, является решением дифференциального уравнения (2).