3.6. Алгоритм кратчайшей раскраски графа

Раскраска представляет собой маркирование вершин графа таким образом, чтобы у смежных вершин маркеры не совпадали. Вместо красок используются числа 0, 1, 2… Условие оптимальности раскрашивания - использование минимального числа красок . Это число называется хроматическим числом графа.

Граф, который можно представить на плоскости без пересечения его рёбер, называется плоским. Так, граф (рис. 3.13) является плоским, т.к. ребро (x₃,x₅) может быть проведено вне контура (x₁,x₂,x₃,x₄,x₅).

Теорема. Для плоских графов .

Пример 3.13. Рассмотрим граф E (рис. 3.13). Убедившись в том, что он – плоский, произведём его раскраску.

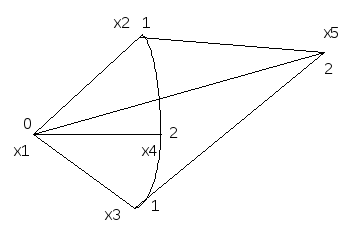
=3 (0,1,2)

Рис.3.13

В общем случае строим таблицу для определения максимальных внутренне-устойчивых подмножеств множества вершин графа, т. е. множеств несмежных вершин графа. Столбцы этой таблицы - номера вершин графа и последний столбец - название очередного максимального внутренне- устойчивого подмножества. Строки таблицы – внутренне-устoйчивые множества.

16

Задача составления пути из дуг-претендентов является переборной. Здесь важно учесть все возможные варианты перебора.

Пример 3.2. Найти кратчайший путь во взвешенном графе (рис.3.2).

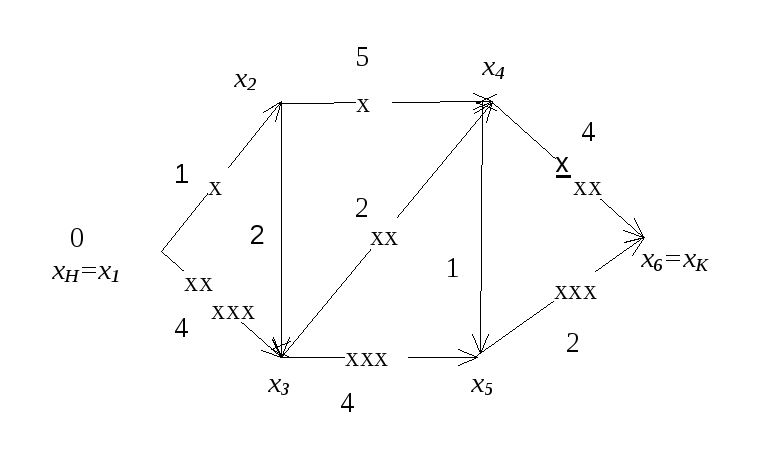
Рис. 3.2

1.

2.M={2}

2.

M={3};;

2.

2.

2.

M={6};

2.

3.

5

(* отмечается дуга, являющаяся претендентом на включение в кратчайший путь)

Процесс решения на 1-ом проходе алгоритма можно оформить в виде таблицы:

Таблица 3.3

x1	x2	x3	x4	x5	x6	M
0						1
0	1	4				2,3
0	1	3	6			3,4
0	1	3	5	7		4,5
0	1	3	5	6	9	5,6
0	1	3	5	6	8	6
0	1	3	5	6	8

На обратном проходе выделяем претендентов. Из них на III проходе строим путь длиной 8. Построен кратчайший путь длиной 8:

Волновой алгоритм построения длиннейшего пути во взвешенном графе.

Используется волновой алгоритм построения кратчайшего пути для взвешенного графа со следующим отличием:

1. В п. 1 волнового алгоритма присваиваем всем вершинам вес 0, тогда автоматически будут строиться длиннейшие пути.

2. В п. 2 алгоритма полагаем .

6

Пример 3.11.

Рис.3.11

3.5.3. Алгоритм построения системы независимых циклов графа

1. Строится произвольный остов графа. В исходном графе отмечаются рёбра, не включенные в остов.

2. Выбирается очередное отмеченное ребро и строится цикл, содержащий это ребро и рёбра остова. Рассмотренное ребро отмечается и, если есть ещё не отмеченные рёбра, то выполняется пункт 2, иначе - пункт 3.

3. По формуле Эйлера (3.2) производится проверка числа построенных циклов.

Пример 3.12

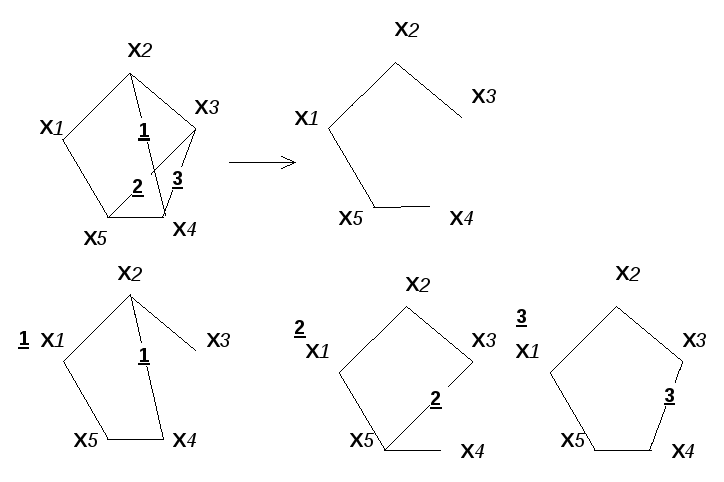Рис 3.12

15

Пример 3.10.

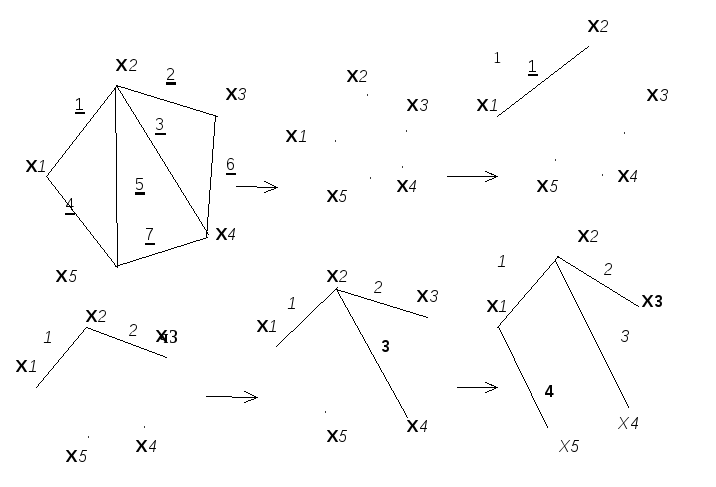
Рис. 3.10

Так как цикл не образовался, то все рёбра с номерами 1, 2, 3, 4 включены в остов. Проверяем по (3.3): m=4, n=5 и 4=5-1.

3.5.2. Алгоритм построения минимального остова

Для взвешенного графа остов с наименьшей суммой весов для вошедших в него рёбер называется минимальным (кратчайшее связное дерево).

Если в сформулированном ранее алгоритме построения обычного остова рассматривать рёбра в порядке возрастания их весов, то будет построен минимальный остов.

14

Пример 3.3. Найти длиннейший путь в графе между вершинами x_н и x_к, используя волновой алгоритм.

Приведем краткое решение задачи поиска длиннейшего пути для графа на рис. 3.3

1. Прямой ход

Рис. 3.3

Таблица 3.4

x1	x2	x3	x4	x5	x6	M
0	0	0	0	0	0	1
0	1	4	0	0	0	2,3
0	1	4	6	0	0	3,4
0	1	4	6	8	0	4,5
0	1	4	6	8	10	5,6
0	1	4	6	8	10	6
0	1	4	6	8	10

2. Обратный ход:

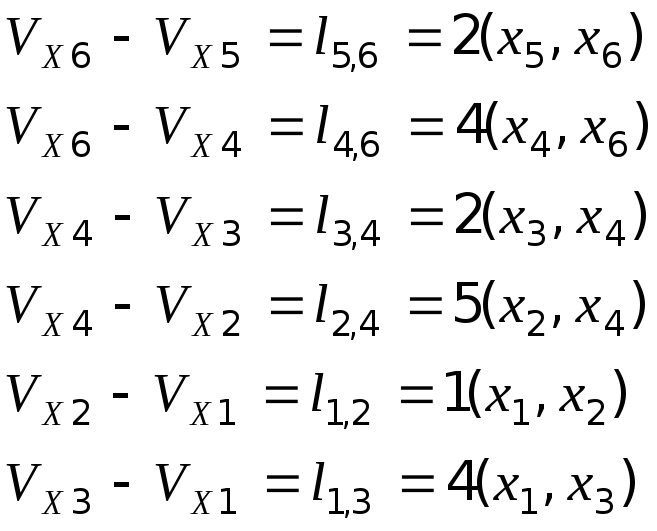
Претенденты (x₁ x₂), (x₁ x₃),(x₂ x₄),(x₃ x₄),(x₃ x₅),(x₄ x₆),(x₅ x₆).

7

3. Построены три длиннейшие пути:

1.

2.

3.