3.3. Нахождение компонент связности

Вершины x_i и x_j слабо связны, если существует путь (x_i, x_j) в графе G=(X,E).

Вершины x_i и x_j сильно связны, если существуют пути (x_i, x_j) и (x_j, x_i).

Если в графе нет путей из x_i в x_j и нет обратного пути из x_j в x_i, то вершины x_i и x_j несвязны. Для неориентированного графа имеет смысл только понятие сильной связности.

Отношение связности рефлексивно, симметрично, транзитивно, т. е. является отношением эквивалентности, и однозначно разбивает множество вершин графа на компоненты связности: максимальные подмножества сильно связанных между собой вершин.

Пример 3.4: Задан граф (рис.3.4). Найти его компоненты связности.

Данный граф может быть разбит на следующие компоненты связности:

1){x1,x2,x3,x4};

2){x5,x6,x7};

3){x8}

Между компонентами - только слабая связность: есть пути из вершин 1-ой компоненты в вершины 2-ой и 3-ей компоненты, а также из вершин 2-ой компоненты в вершину 3-ей.

Рис. 3.4

Алгоритм построения компонент связности в неориентированном графе

1. i=0. Все вершины графа не отмечены.

2. i=i+1. Выбираем очередную неотмеченную вершину, отмечаем её и все связанные с нею вершины значением индекса i с помощью распространения волны отметок по ребрам, идущих от уже отмеченных индексом i вершин. Таким образом выделяется i компонента связности. Если есть ещё неотмеченные вершины, то выполняется п.2, иначе выделение компонент связности закончено.

8

Пример 3.9.

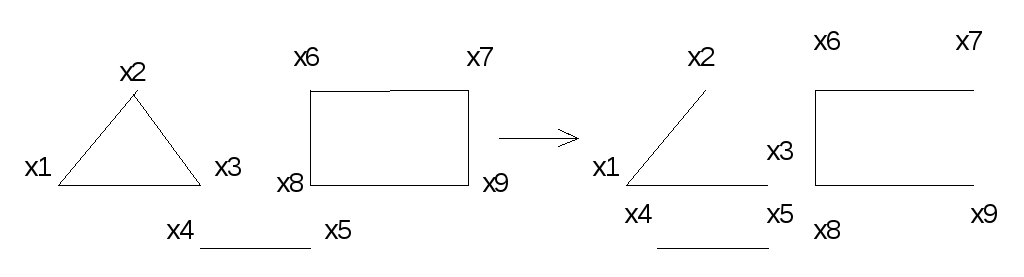
Рис. 3.9

3.5.1. Алгоритм построения произвольного остова

1. Для каждой компоненты i графа выполняем пункты 2 и 3.

2. Строим частичный подграф, содержащий все n_i вершин i-й компоненты и не содержащий ребер (0- граф).

3. Если в текущий частичный граф включены уже n_i-1 ребер, то остов для компоненты i построен, иначе выбираем очередное ребро компоненты и пытаемся его включить в текущий граф.

Если в текущем графе это не приводит к образованию цикла, то включаем ребро, иначе - не включаем.

Ребро считаем рассмотренным.

Выполняем пункт 3.

13

Пример 3.7

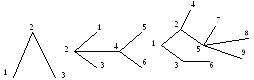
Рис. 3.7

Остов - это подграф (частичный граф), который может быть построен из графа удалением некоторых ребер и который является деревом.

В общем случае для графа можно построить несколько остовов. Для приведенного ниже графа построен один из возможных вариантов остова.

Пример 3.8.

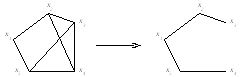
Рис. 3.8

Для несвязного графа рассматриваются отдельные его компоненты. Остов такого графа - совокупность его компонент.

12

Пример 3.5

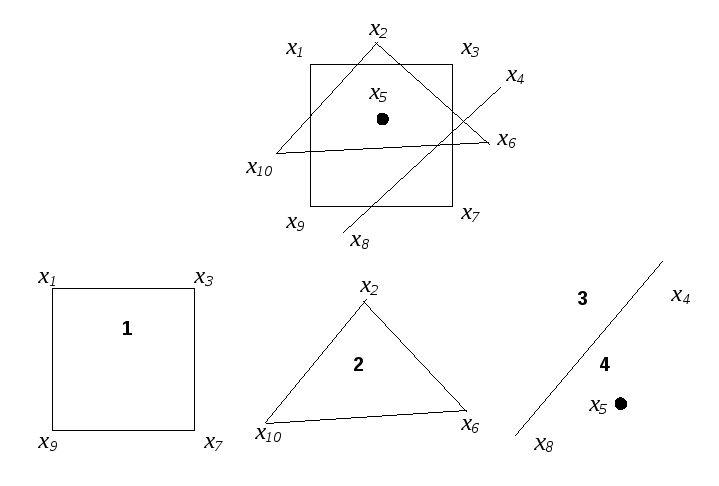
Рис. 3.5

Решение:

1. i=0

2. i=1. Отмечаем индексом i=1 вершину x₁ и связанные с ней вершины x₃, x₇ и x₉. Получена первая компонента связности: k₁ {x₁,x₃,x₇,x₉ }

2. i=2. Отметим индексом i=2 вершину x₂ и вершины x₆,x₁₀. Построена вторая компонента связности:k₂ {x₂,x₆,x₁₀}

2. i=3. Отмечаются индексом i=3 вершины x₄ и x₈ . Построена третья компонента связности: k₃ {x₄, x₈ }.

2. i=4. Отмечаются индексом i=4 вершину x₅, которая формирует четвертую компоненту связности – k₄ {x₅}

3.4. Алгоритмы нахождения подграфов

Циклом называется замкнутый маршрут в неориентированном графе. Для ориентированного графа определяется аналогично понятие контур - замкнутый путь.

9

Пример 3.6. В графе (рис.3.6) каждому ребру присвоен свой номер. Выделим соответствующее ему число циклов. Для нашего примера циклами C_i являются замкнутые маршруты, образованные ребрами : C₁={1, 2, 5, 4}, C₂={5, 6, 7}, C₃={3, 6, 2}, C₄={1, 2, 6, 7, 4} и т. д. Среди этих циклов найдутся такие, которые включают в себя другие циклы. Так, цикл C₄ состоит из циклов C₁ и C₂ , у которых имеется общее ребро 5, не вошедшее в цикл 4. Говорят, что цикл 4 получен линейной комбинацией циклов 1 и 2, т. е. является линейно зависимым от них.

Рис. 3.6

Линейнозависимым от некоторой совокупности других циклов называется цикл, который можно построить линейной комбинацией циклов в этой совокупности.

Присвоим каждому ребру графа номерj, j=1,m и сопоставим каждому циклу С_i двоичный m-разрядный вектор V_i , компоненты v_ij которого определяются следующим образом: v_ij = 0, если ребро j не входит в цикл C_i , v_ij = 1 - в противном случае.

Тогда линейной комбинацией векторов V_i является результат векторной операции сложения по модулю два этих векторов.

Поскольку V_i - отношение принадлежности рёбер графа циклу C_i , а C_i - это множество рёбер, то в результате применения векторной операции мы получаем совокупность рёбер, входящих в циклы, составляющих линейную комбинацию за исключением общих для этих циклов рёбер.

10

На языке теории множеств это означает объединение множеств C_i без их пересечения, что соответствует операции «симметрическая разность» двух множеств.

j	1	2	3	4	5	6	7
V1	1	1	0	1	1	0	0
	
V2	0	0	0	0	1	1	1
V4	1	1	0	1	0	1	1

В нашем примере общим является ребро 5, которое исключено из цикла 4.

Линейно-независимым от совокупности других циклов называется цикл, который не может быть построен линейной комбинацией этих циклов.

Максимальное множество линейно-независимых циклов образует систему независимых циклов; мощность  этого множества называется цикломатическим числом. Это число определяется по формуле Эйлера

=m-n+p (3.2)