Лінійна алгебра

21

		1		1
e1	=				,				.
		2
				2

Аналогічно знайдемо властивий вектор для λ2 = 4

−x1 − x2 = 0,−x1 − x2 = 0.

Другим властивим вектором буде l2 = (−1,1). Властивий вектор одиничної довжини має вигляд

	−1			1
e2	=				,				.
			2
				2

Звернемо увагу на те, що вектори e1 і e2 перпендикулярні (рис. 13.1):

e	e	=	1				−1			+	1				1			= 0.
1	2	2			2				2				2
Ця властивість має місце і в загалиному випадку.
Теорема. Якщо матриця A порядку														n симетрична, то її властиві

вектори, які відповідають різним властивим значенням, перпендикулярні. Якщо не всі корені характеристичного рівняння різні, тобто деяке властиве значення повторюється k разів, то можна вказати k взаємно ортогональних властивих векторів, які відповідають цьому властивому значенню.

Таким чином, в просторі Rn можна скласти базис з властивих векторів матриці A. Вектори базису взаємно перпендикулярні. Якщо довжини всіх векторів базису дорівнюють одиниці, то базис називається декартовим.

Приклад 12.2. Знайти матрицю оператора A з прикладу 12.1 в базисі з її властивих векторів e1 та e2 .

Розв’язання. Запишемо матрицю переходу (її стовпці є координатами векторів e1 і e2 ):

		1				−1
		2		2
	B =								.
		1		1
		2		2

Матриця B є матриця переходу від одного декартового базису i , j до іншого декартового базису e1, e2 (рис. 13.1).

Матриця оператора в новому базисі обчислюється за формулою (11.1):

														22
					1		1											1				−1
														3 −1												2		0
					2		2											2		2
′	= B	−1	AB =
A					−1		1							−1 3			1					1				=	0	4	.
					2		2											2		2

Матриця A′ має більш простий вигляд: на головній діагоналі записані властиві значення, а всі інші елементи дорівнюють нулю.

Матриця, в якій всі елементи, що відмінні від головної діагоналі, дорівнюють нулю, називається діагональною.

В загальному випадку справедливі наступні теореми.

Теорема 12.1. Для кожної симетричної матриці A порядку n можна

підібрати таку ортогональну матрицю B, для якої матриця A′ = B−1AB буде діагональною, причому на головній діагоналі будуть стояти властиві значення матриці A.

Стовпці матриці B складаються з декартового базису властивих

векторів матриці A.

Теорема 12.2. Матриця B переходу від одного декартового базису до

іншого є ортогональною, тобто такою, що її обернена матриця B−1 збігається з транспонованою BT : B−1 = BT .

Зворотно, якщо матриця переходу ортогональна, то з декартового базису обов'язково вийде декартовий базис.

13. КВАДРАТИЧНІ ФОРМИ

Означення. Квадратичною формою змінних x1 та x2 називається вираз

F(x1,x2 ) = a11x12 + 2a12 x1x2 + a22 x22 ,

де a11, a12 і a22 – задані числа.

Матрицею цієї квадратичної форми називається матриця

A = a11 a12 .

a12 a22

Якщо позначити

x			= (x1 x2 ),
x = 1		, xT
x2

то квадратичну форму F(x1,x2 ) можна записати в матричному вигляді

F = xT Ax.

Виконаємо заміну змінних

x = Bx′.

Тоді, враховуючи, що

xT = x′T BT ,

23

отримаємо квадратичну форму

F = x′T BT ABx′

з новою матрицею
′	= B	T	AB.	(13.1)
A

Якщо B – ортогональна матриця, то (13.1) збігається з формулою (11.1). За теоремами 12.1 та 12.2 матрицю B можна підібрати так, щоб матриця A′ була діагональною, де на головній діагоналі стоять властиві значення матриці A. Тоді квадратична форма F з новими змінними x1′ та x1′ буде мати вигляд

	F = λ						(x′)2			+ λ (x′ )2 .										(13.2)
			1				1			2		2
Вираз (13.2) називається квадратичною формою в канонічному вигляді.
Наведені відомості про квадратичні форми з двома змінними																				x1 та x2
узагальнюються і на більшу кількість змінних.
Приклад. Звести криву другого порядку
3x2 − 2xy + 3y2 − 4x − 4y −12 = 0																				(13.3)
до кананічного вигляду і побудувати її.
Розв’язання. Розглянемо квадратичну форму
F (x, y) = 3x2 − 2xy + 3y2 .
Для матриці A цієї квадратичної форми в												прикліді 12.1 були								знайдені
властиві значення λ1 = 2 і λ2			= 4 та відповідні їм властиві вектори
	1		1									−1				1
e1 =				,					і	e2 =					,				.
	2											2				2
						2

В прикладі 12.2 знайдено матрицю													B						переходу від базису i , j до
базису e1, e2 :
									1				−1
									2				2
				B =														.
									1				1
									2				2
Виконавши заміну змінних
					x							X
									= B						,
					y							Y
тобто
x =	1			X −	1			Y, y =							1						X +	1			Y ,
2			2															2			2

квадратичну форму зведемо до виду

F= 2X 2 + 4Y2 ,

адоданки першого степеня приймуть вигляд

24

−4x − 4y = −4 X + 4 Y − 4 X − 4 Y = −8 X = −42X .

2 2 2 2 2

Отже, рівняння (13.3) можна записати так

2X 2 + 4Y2 − 42X −12 = 0 чи X 2 + 2Y2 − 22X = 6. Доповняючи вираз до повного квадрату, отримаємо

X 2 − 2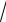2X = X 2 − 22X + 2 − 2 = (X − 2)2 − 2.

Отже, якщо вісь OX направити вздовж вектора e1, а вісь OY – вздовж вектора e2 (рис. 13.1), то в новій системі координат XOY рівняння (13.3) можна записати у вигляді:

(X − 2)2 + 2Y2 − 2 = 6, або (X − 2)2 + 2Y2 = 8.

Поділивши обидві частини останнього рівняння на 8, отримаємо рівняння еліпса

(X − 2)2 + Y2 =1

84

зцентром в точці X = 2 , Y = 0 і півосями a = 8 = 22 , b = 2. Еліпс зображено на рис. 13.2. Можна позначити

Χ= X − 2

і записати рівняння еліпса в канонічному вигляді

Χ2

Y2

+

=1.

(2

)2

22

2

x2

y

X

Y

2

2

e2

2

j

e1

x1

O

x

O

i

Рис. 13.1

Рис. 13.2

ЛІТЕРАТУРА

1.Мышкмс А.Д. лекции по высшей математике. М.: Наука, 1969. – 640 с.

2.Глаголев А.А.,Солнцева Т.В. Курс высшей математики. М.:Высшая школа, 1971. – 654 с.